- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
CIE A Level Maths: Probability & Statistics 2复习笔记2.3.1 Probability Density Function
Calculating Probabilities using PDF
What is a probability density function (p.d.f.)?
- For a continuous random variable , it is often possible to model probabilities using a function
- This function is called a probability density function (p.d.f.)
 The graph does not need to start and end on the x-axis
The graph does not need to start and end on the x-axis
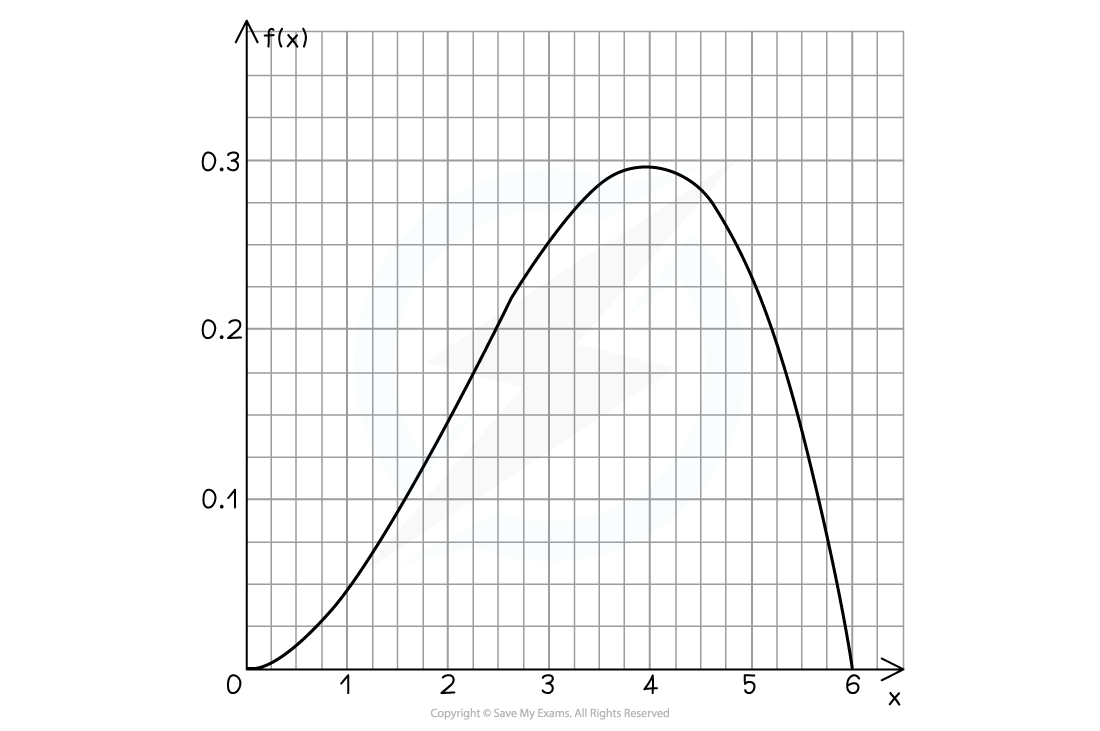
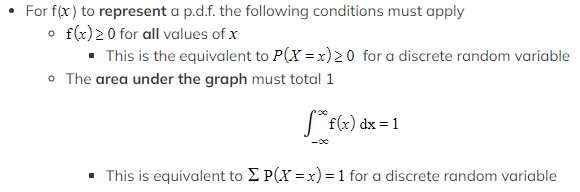 How do I find probabilities using a probability density function (p.d.f.)?
How do I find probabilities using a probability density function (p.d.f.)?
 How do I solve problems using the PDF?
How do I solve problems using the PDF?
- Some questions may ask for justification of the use of a given function for a probability density function
 Worked Example
Worked Example

![]()

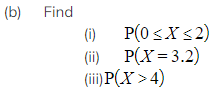

Exam Tip
- If the graph is easy to draw, then a sketch of f(x) is helpful
- This can highlight useful features such as the graph (and so probabilities) being symmetrical
- Some p.d.f. graphs lead to common shapes such as triangles or rectangles whose areas are easy to find, avoiding the need for integration
Median and Mode of a CRV
What is meant by the median of a continuous random variable?
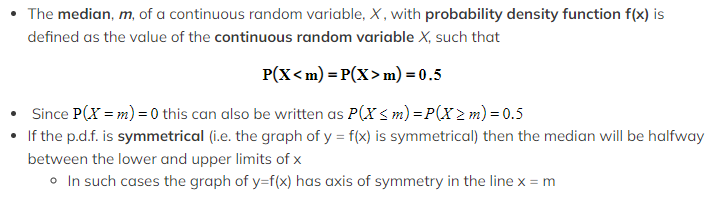 How do I find the median of a continuous random variable?
How do I find the median of a continuous random variable?
 How do I find quartiles (or percentiles) of a continuous random variable?
How do I find quartiles (or percentiles) of a continuous random variable?
- In a similar way, to find the median
- The lower quartile will be the value L such that P(X ≤ L) = 0.25 or
P(X ≥ L) = 0.75 - The upper quartile will be the value U such that P(X ≤ U) = 0.75 or
P(X ≥ U) = 0.25
- The lower quartile will be the value L such that P(X ≤ L) = 0.25 or
- Percentiles can be found in the same way
- The 15th percentile will be the value k such that P(X ≤ k) = 0.15 or
P(X ≥ k) = 0.85
- The 15th percentile will be the value k such that P(X ≤ k) = 0.15 or
What is meant by the mode of a continuous random variable?
- The mode of a continuous random variable, X , with probability density function f(x) is the value of x that produces the greatest value of f(x) .
How do I find the mode of a PDF?
- This will depend on the type of function f(x); the easiest way to find the mode is by considering the shape of the graph of f(x)
- If the graph is a curve with a (local) maximum point, the mode can be found by differentiating and solving the equation f'(x) = 0
- If there is more than one solution to f'(x) = 0 , further work may be needed to deduce which answer is the mode
- Look for valid values of from the definition of the p.d.f.
- Use the second derivative (f'' (x) ) to deduce the nature of each stationary point
- You may need to check the values of f(x) at the endpoints too
- If there is more than one solution to f'(x) = 0 , further work may be needed to deduce which answer is the mode
- If the graph of y = f(x) is symmetrical, symmetry may be used to deduce the mode
- For a symmetrical p.d.f. median = mode = mean
(See E(X) & Var (X) (continuous) for the mean)
Worked Example (a)Find the median of X, giving your answer to three significant figures
(a)Find the median of X, giving your answer to three significant figures
(b)Find the exact value of the mode of X
(a)Find the median of X, giving your answer to three significant figures
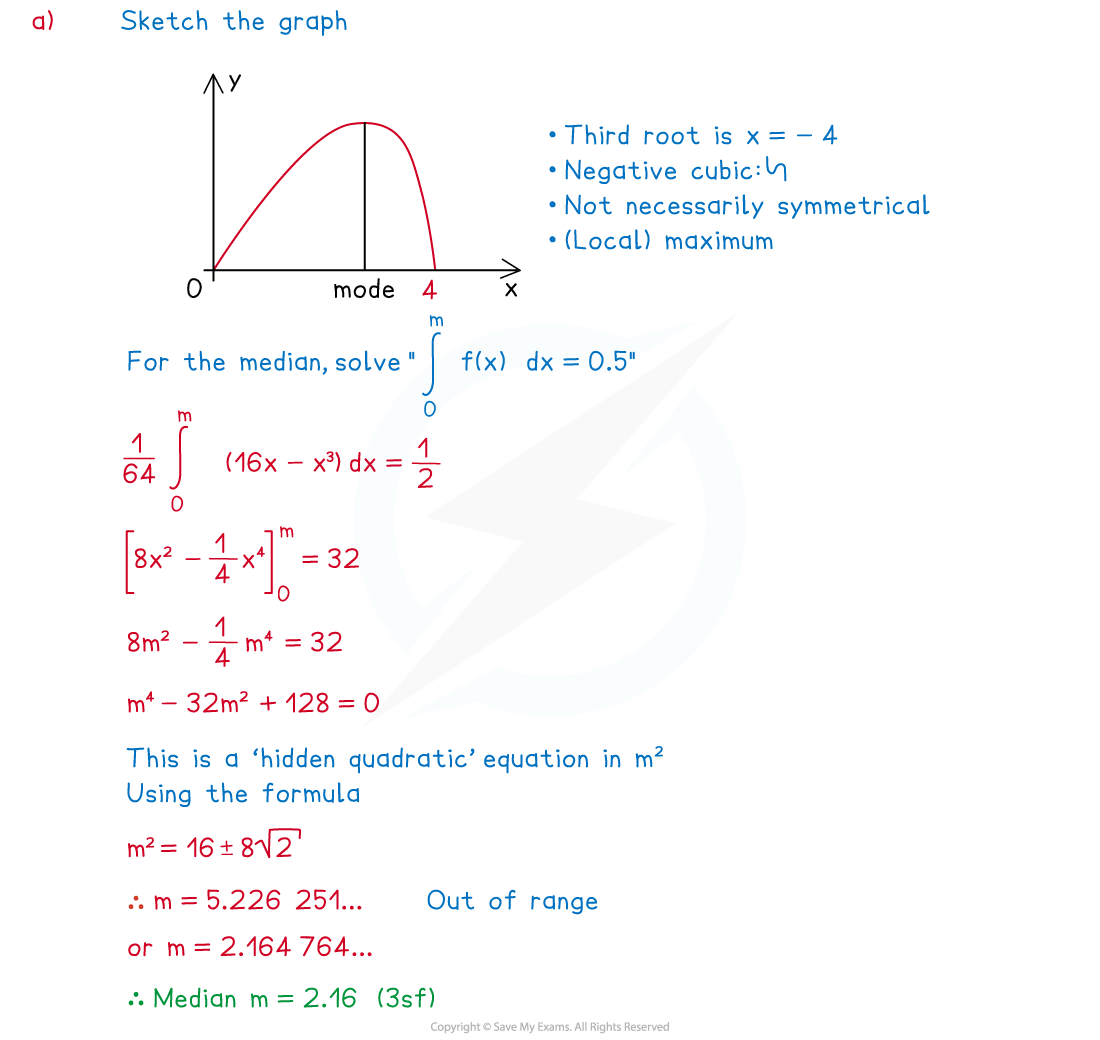
(b)Find the exact value of the mode of X

Exam Tip
- Avoid spending too long sketching the graph of y = f(x), only do this if the graph is straightforward as finding the median and mode by other means can be just as quick
转载自savemyexams

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








