- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
CIE A Level Maths: Probability & Statistics 2复习笔记2.2.1 Linear Combinations of Random Variables
aX+b
How are the mean and variance of X related to the mean and variance of aX + b?
- If a and b are constants then the following results are true
- E(aX + b) = aE(X) + b
- Var(aX + b) = a² Var(X)
- Note that the mean is affected by multiplication and addition whereas addition does not change the variance
- The factor of a² includes the squared because the values of X are squared in the calculation
- You could try and use the first result and the formula for variance to verify the second result
- Remember a subtraction can be written as an addition
- X – b can be written as X + (-b)
- And division can be written as a multiplication
 What does the distribution of aX + b look like?
What does the distribution of aX + b look like?
- A linear function is applied to each value of X
- The graphical representation of aX + b is a linear transformation (a translation and a stretch) of the graphical representation of X
- If X follows a normal distribution then aX + b will also follow a normal distribution
- If X ~ N(μ, σ²) then aX + b ~ N(aμ + b, a²σ²)
- If X follows a binomial, geometric or Poisson distribution then aX + b will no longer follow the same type of distribution
Worked Example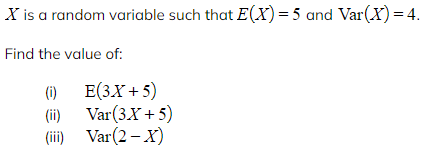

aX + bY
How are the means and variances of X and Y related to the mean and variance of X + Y ?
- If X and Y are two random variables then X + Y is the random variable whose values are the sums of each pair containing one value of X and one value of Y
- E(X + Y) = E(X) + E(Y)
- this is true for any random variables X and Y
- Note that E(X – Y) = E(X) - E(Y) (see below for more information)
- Var(X + Y) = Var(X) + Var(Y)
- this is true if X and Y are independent
- Note that Var(X - Y) = Var(X) + Var(Y) (see below for more information)
What does the distribution of X + Y look like?

What does the distribution of aX + bY look like?
- If X and Y are random variables and a and b are two constants we can combine the results for aX + b and X + Y
- E(aX + bY) = aE(X) + bE(Y)
- this is true for any random variables X and Y
- Var(aX + bY) = a²Var(X) + b²Var(Y)
- this is true if X and Y are independent
- Note that b is squared for the variance so we have
- E(aX - bY) = aE(X) - bE(Y)
- Var(aX - bY) = a²Var(X) + b²Var(Y)
- Notice that the variances of aX + bY and aX – bY are the same
- If X and Y are two independent normal distributions then aX + bY is also a normal distribution
- If X ~ N(μ1, σ1²) and Y ~ N(μ2, σ2²) then aX ± bY ~ N(aμ1 ± bμ2, a²σ1² + b²σ2²)
- Note that aX + bY is no longer Poisson even if X and Y are Poisson
- This holds provided a and b are not 0 or 1
Worked Example
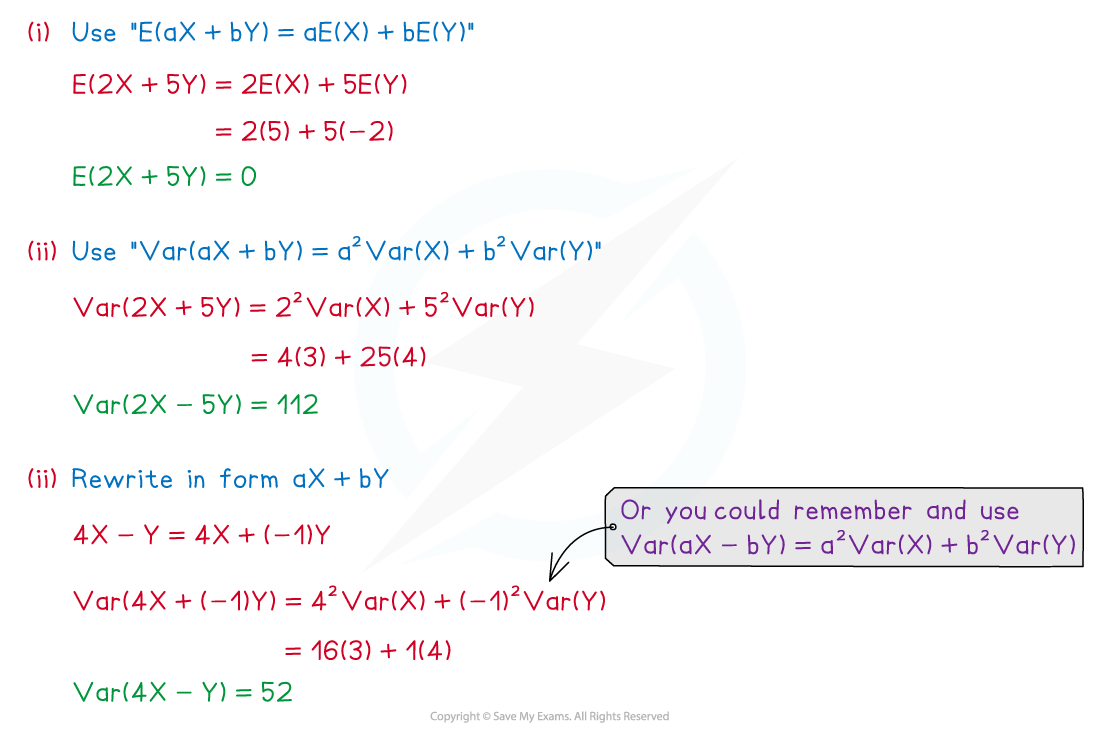
Linear Combinations
For a given random variable X, what is the difference between 2X and X1 + X2?
- 2X means one observation of X is taken and then doubled
- X1 + X2 means two observations of X are taken and added together
- 2X and X1 + X2 both have the same expected value of 2E(X)
- 2X and X1 + X2 have different variances
- Var(2X) = 2²Var(X) = 4Var(X)
- Var(X1 + X2) = 2Var(X)
- Imagine X could take the values 0 and 1
- 2X could then take the values 0 and 2 (2 × 0 = 0 and 2 × 1 = 2)
- X1 + X2 could then take the values 0, 1 and 2 (0 + 0 = 0, 0 +1 = 1, 1 + 1 = 2)
- Sometimes questions may describe the variables in context
- The mass of a carton of half a dozen eggs is the mass of the carton plus the mass of the 6 individual eggs and can be modelled using the random variable
- C + E1 + E2 + E3 + E4 + E5 + E6 where
- C is the mass of a carton
- E is the mass of an egg
- It is not C + 6E because the masses of the 6 eggs could be different
How do I use linear combinations of normal random variables to find probabilities?
- If the random variables are normally distributed and independent you might be asked to find probabilities such as
- P(X1 + X2 + X3> 2Y + 5)
- This could be given in words
- Find the probability that the mass of three chickens (X) is more than 5 kg heavier than double the mass of a turkey (Y)
- To solve these problems:
- STEP 1: Rearrange the inequality to get all the random variables on one side
- P(X1 + X2 + X3– 2Y > 5)
- STEP 2: Find the mean and variance of the combined normal random variable
- μ = E(X1 + X2 + X3– 2Y) = E(X1) + E(X2) + E(X3) - 2E(Y)
- σ² = Var(X1 + X2 + X3– 2Y) = Var(X1) + Var(X2) + Var(X3) + 2² Var(X1)
- STEP 3: Find the required probability using the combined normal distribution
- X1 + X2 + X3– 2Y ~ N(μ, σ²)
- Use z-values and the table of values
- STEP 1: Rearrange the inequality to get all the random variables on one side
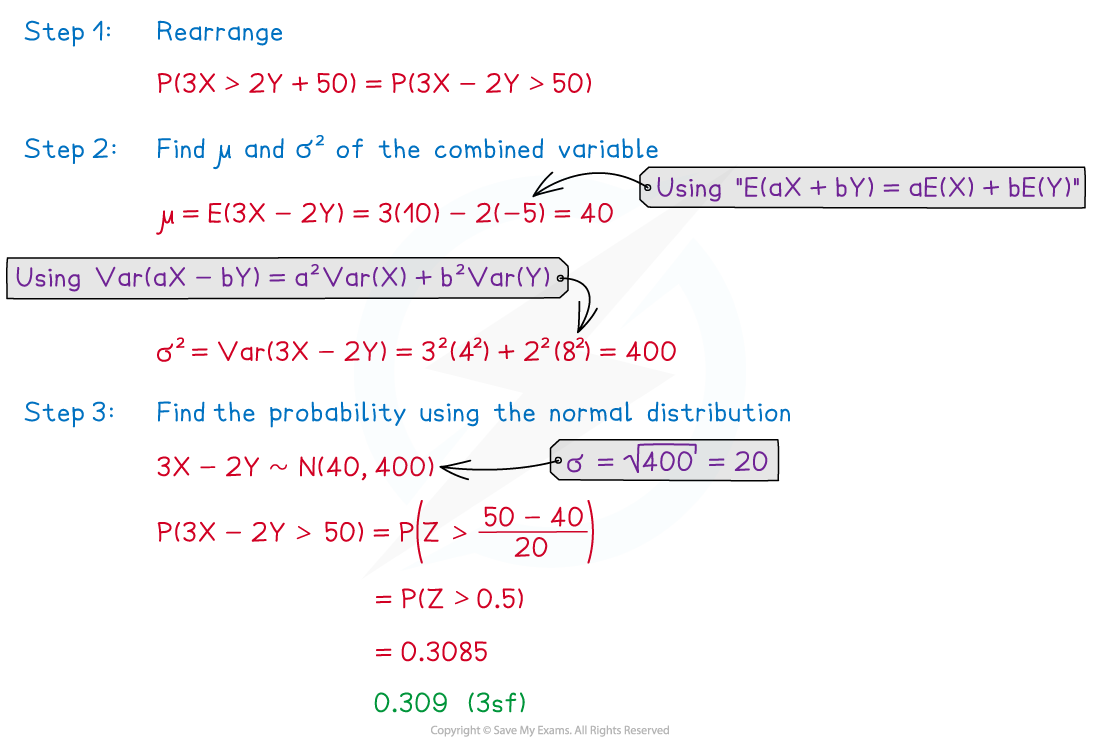
Worked Example
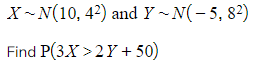
Exam Tip
- Be careful with negatives!
转载自savemyexams

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









