- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
CIE A Level Maths: Probability & Statistics 1复习笔记3.4.2 Normal Approximation of Binomial
Normal Approximation of Binomial
When can I use a normal distribution to approximate a binomial distribution?
Why do we use approximations?
- If there are a large number of values for a binomial distribution there could be a lot of calculations involved and it is inefficient to work with the binomial distribution
- These days calculators can calculate binomial probabilities so approximations are no longer necessary
- However it is easier to work with a normal distribution
- You can calculate the probability of a range of values quickly
- You can use the inverse normal distribution function (most calculators don't have an inverse binomial distribution function)
- In your exam you must use the formula and not a calculator to find binomial probabilities so you are limited to small values of n
What are continuity corrections?
- The binomial distribution is discrete and the normal distribution is continuous
- A continuity correction takes this into account when using a normal approximation
- The probability being found will need to be changed from a discrete variable, X, to a continuous variable, XN
 How do I apply continuity corrections?
How do I apply continuity corrections?
- Think about what is largest/smallest integer that can be included in the inequality for the discrete distribution and then find its upper/lower bound

How do I approximate a probability?
- STEP 1: Find the mean and variance of the approximating distribution
 Worked Example
Worked Example


Exam Tip
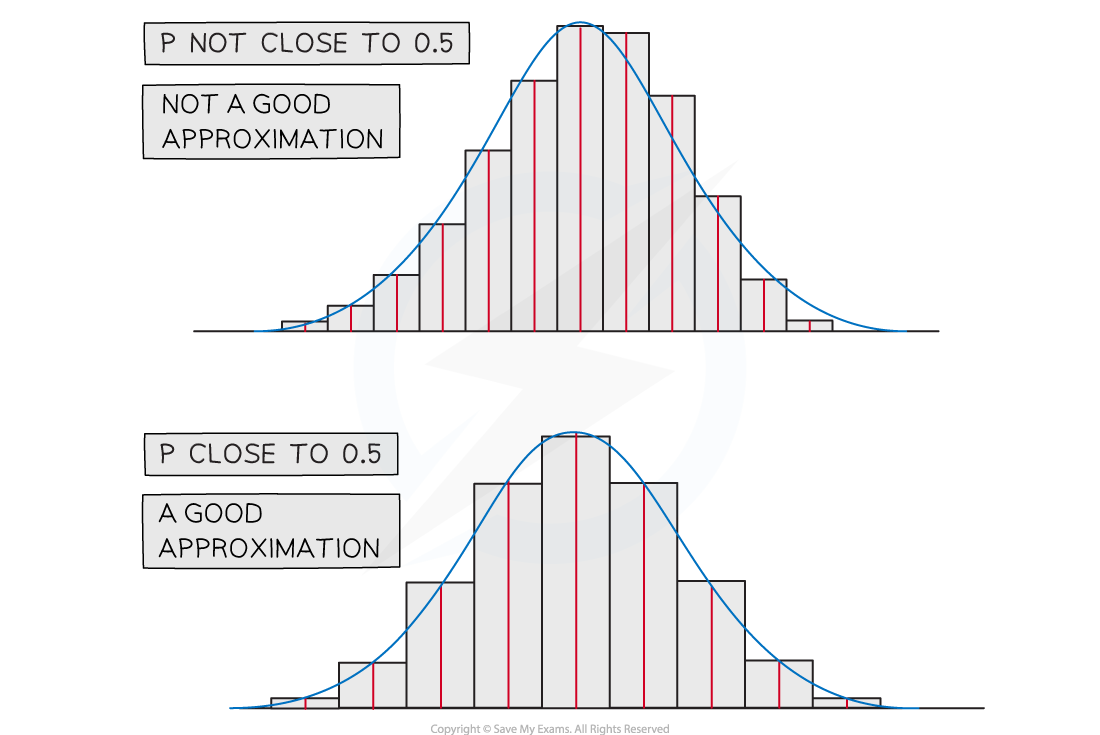
- In the exam, the question will often tell you to use a normal approximation but sometimes you will have to recognise that you should do so for yourself. Look for the conditions mentioned in this revision note, n is large, p is close to 0.5, np > 5 and nq > 5.
转载自savemyexams

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1