CIE A Level Maths: Probability & Statistics 1复习笔记2.2.1 Arrangements & Factorials
Arrangements
How many ways can n different objects be arranged?
- When considering how many ways you can arrange a number of different objects in a row it’s a good idea to think of how many of the objects can go in the first position, how many can go in the second and so on
What happens if the objects are not all different?
- Consider arranging two identical objects, although there are still two different ways you could place the objects down next to each other, the arrangements would look exactly the same
-
- To arrange the letters A1 and A2 we have
- A1 A2 and A2 A1
- These are exactly the same, so there is only one way to arrange the letters A and A
- To arrange the letters A1, A2 and C we have
- A1 A2 C, A2 A1 C, A1 C A2, , A2 C A1, C A1 A2, C A2 A1
- Although the two letter As were placed separately, they are identical and so each pattern has been repeated twice
- There are 6 ways to arrange the letters A, A and C, but with some duplicates
- To arrange the letters A1 and A2 we have
-
If there are two identical objects within a group of objects to be arranged, the number of ways of arranging different objects should be divided by 2
- Consider arranging three identical objects, although there are still six different ways you could place the objects down next to each other, the arrangements would look exactly the same
-
- To arrange the letters A1, A2 and A3
- A1 A2 A3 , A1 A3 A2 , A2 A1 A3 , A2 A3 A1 , A3 A1 A2 , A3 A2 A1
- However, if these were all A, we would have AAA repeated six times
- To find the number of arrangements of the letters A, A, A and C we would have to consider the number of ways of arranging four letters if they were all different and then divide by the number of ways AAA is repeated
- To arrange the letters A1, A2 and A3
Worked Example
By considering the number of options there are for each letter to go into each position, find how many different arrangements there are of the letters in the word REVISE.
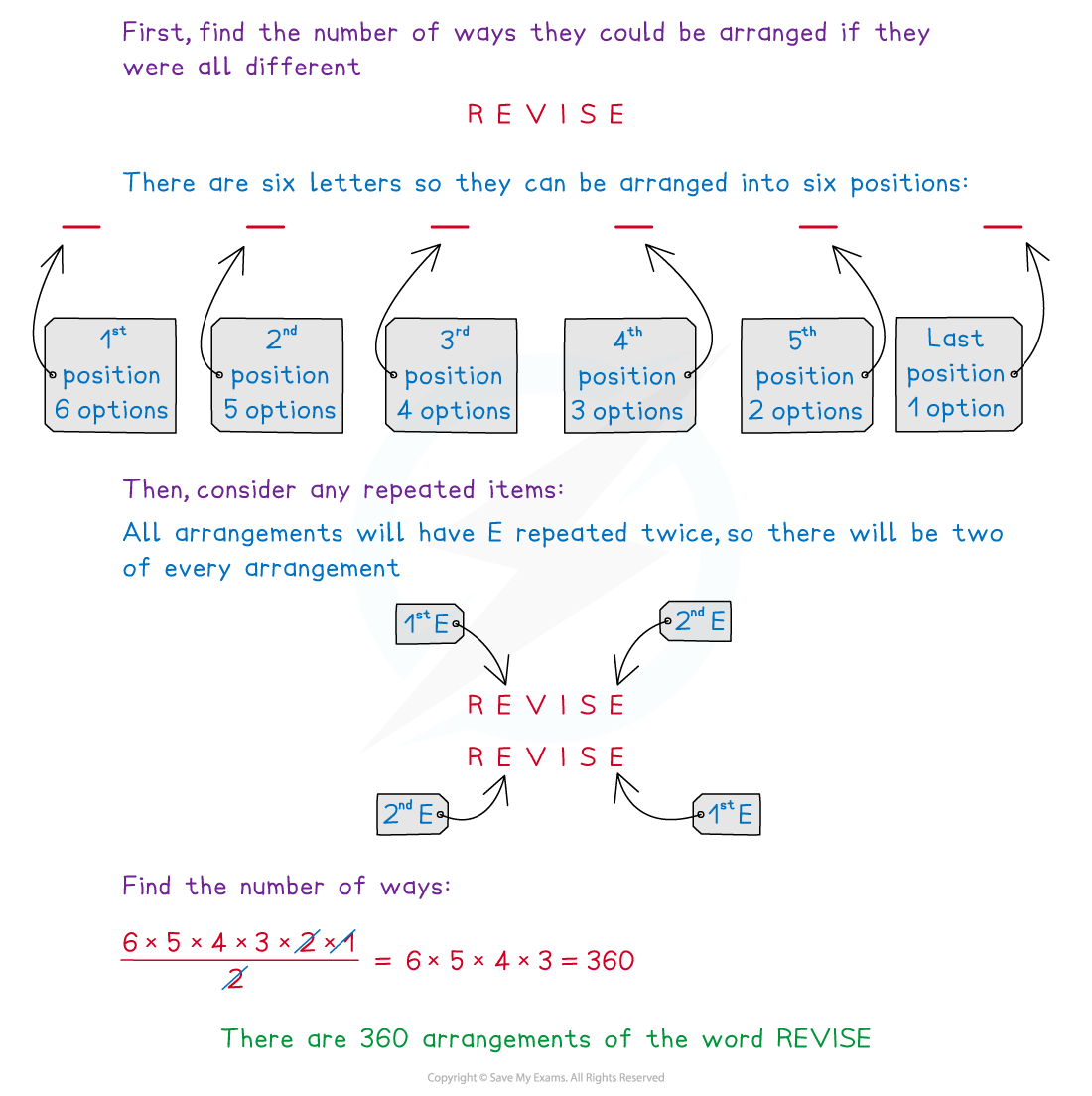
Factorials
What are factorials?
- Factorials are a type of mathematical operation (just like +, -, ×, ÷)
- The symbol for factorial is !
How are factorials and arrangements linked?
What are the key properties of using factorials?
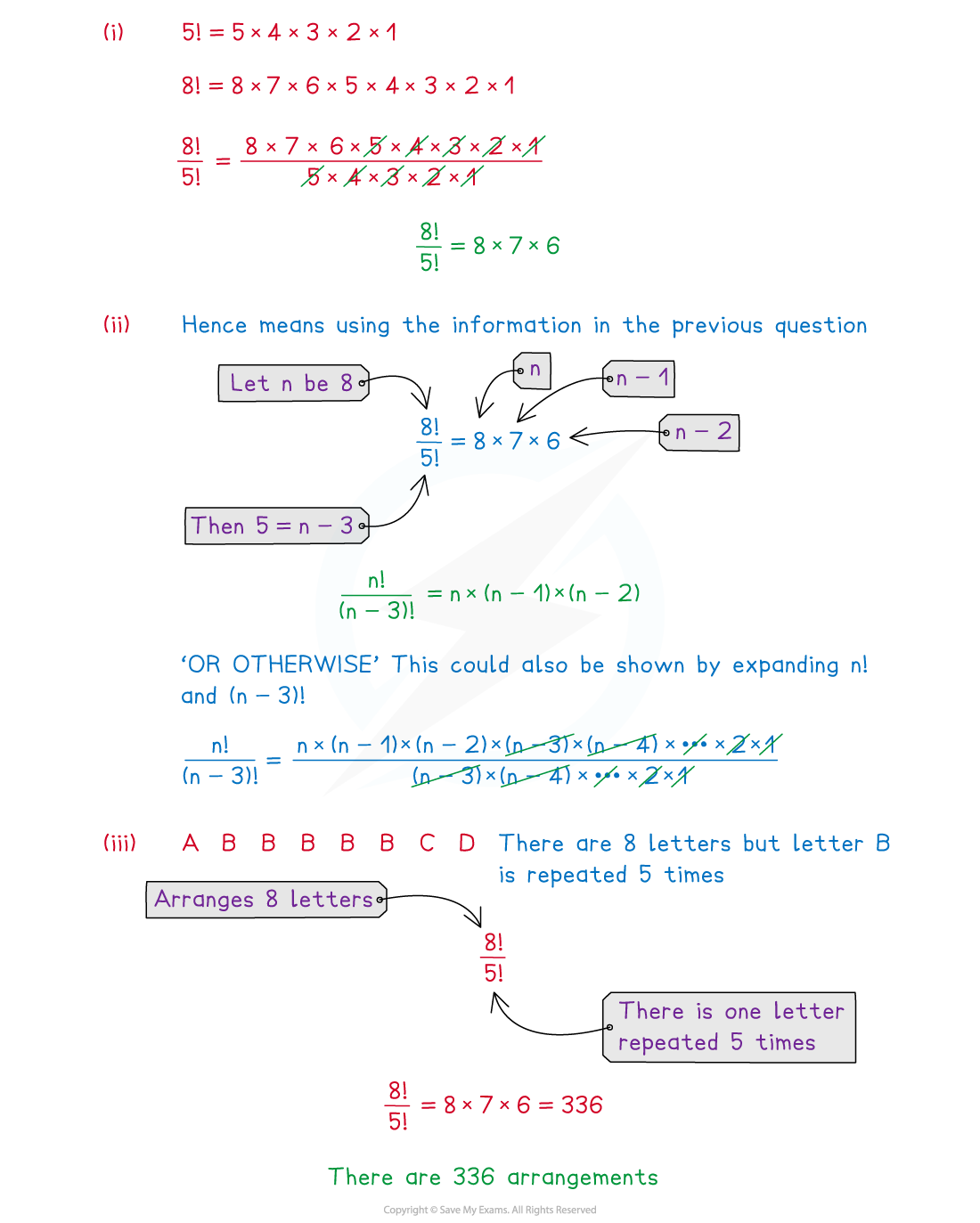
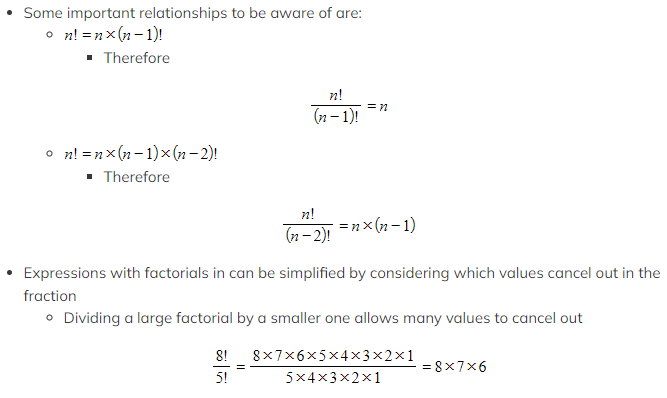Worked Example
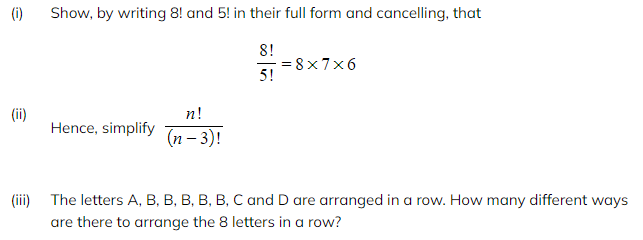
Exam Tip
- Arrangements and factorials are tightly interlinked with permutations and combinations. Make sure you fully understand the concepts in this revision note as they will be fundamental to answering perms and combs exam questions.
转载自savemyexams
翰林AMC8视频课重磅上线！
国际竞赛真题资源免费领取
