CIE A Level Maths: Mechanics复习笔记3.2.4 Connected Bodies - Pulleys

What is a pulley (or peg)?

• A pulley is a wheel like device that rotates as a string passes over it allowing motion of any particles attached to the string
  • The term ‘string’ can refer to any rope, cable or chain
  • Strings can be assumed to be light and inextensible
• Pulleys allow a (inextensible) string to change its orientation.
• In A level mathematical models, pulleys will always be smooth and light, so there is no friction involved at the pulley and its mass is negligible
• A peg is similar to a pulley but is a fixed point that a particle can be suspended from (like a nail in a wall)

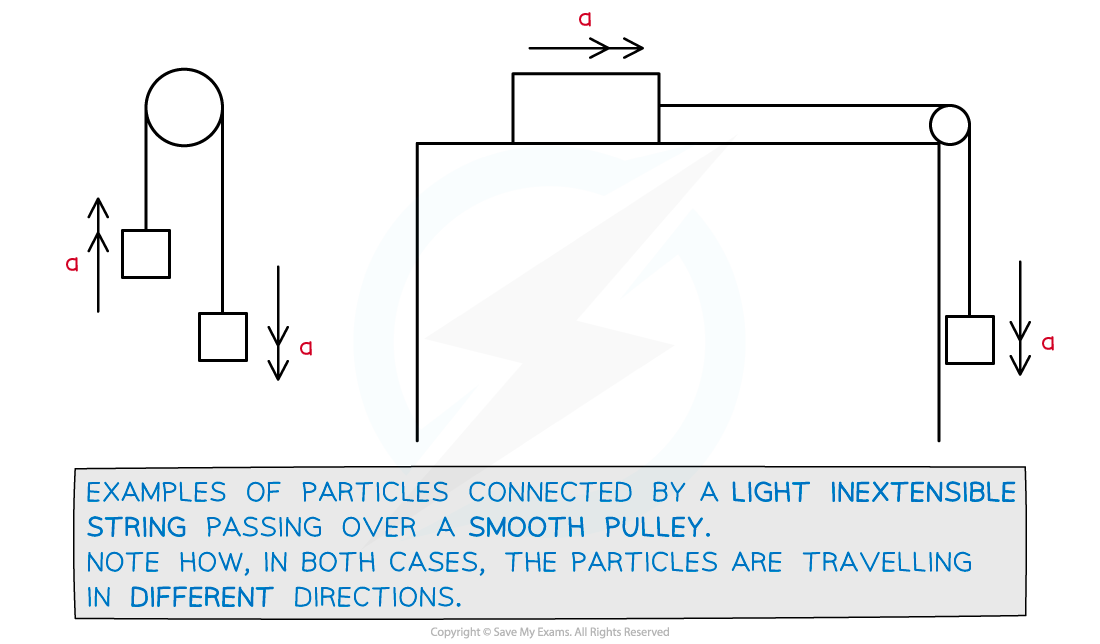
How do I solve pulley questions?

• In all pulley questions the particles are moving in different directions so it is best if they are considered separately as opposed to treating them as one object
• If a particle is in motion in the direction being considered then Newton’s Laws of Motion apply so use “F = ma” (N2L)
• For constant acceleration the ‘suvat’ equations could be involved
• Step 1. Draw a series of diagrams
  • Label the forces and the positive direction of motion for each particle.
  • Colour coding forces acting on each particle may help

  

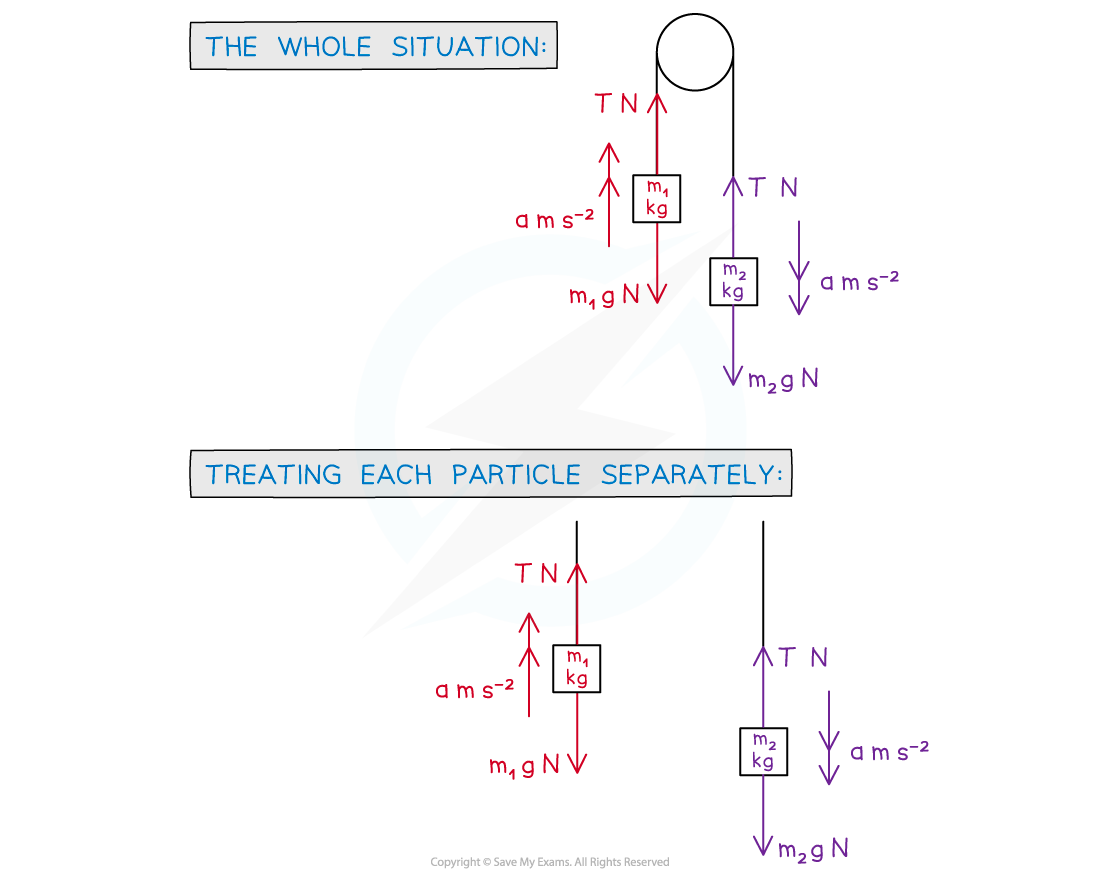
• Step 2. Write equations of motion, using “F = ma”
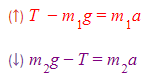
  • Equations 1 and 2: Treating each particle separately

• Step 3. Solve the relevant equation(s) and answer the question
  • Some trickier problems may lead to simultaneous equations

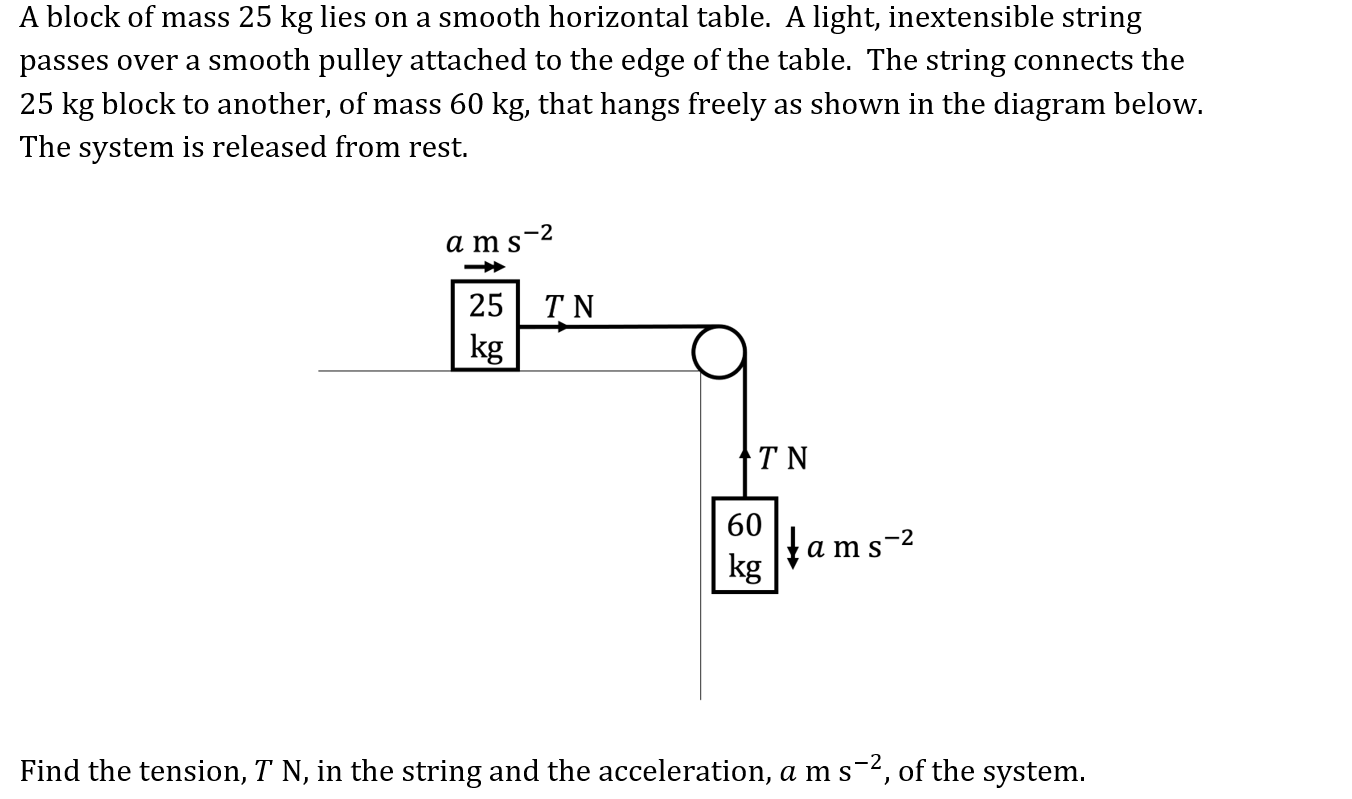
Find the tension, T N , in the string and the acceleration, a m s^-2 , of the system.