- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
CIE A Level Physics复习笔记20.2.4 Faraday's & Lenz's Laws
Faraday's & Lenz's Laws
- Faraday’s law tells us the magnitude of the induced e.m.f in electromagnetic induction and is defined as:
The magnitude of the induced e.m.f is directly proportional to the rate of change in magnetic flux linkage
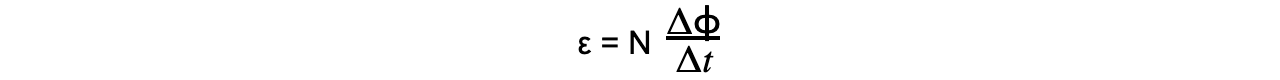
- Where:
- ε = induced e.m.f (V)
- N = number of turns of coil
- Δɸ = change in magnetic flux (Wb)
- Δt = time interval (s)
- Lenz’s Law gives the direction of the induced e.m.f as defined by Faraday’s law:
The induced e.m.f acts in such a direction to produce effects which oppose the change causing it
- Lenz’s law combined with Faraday’s law is:
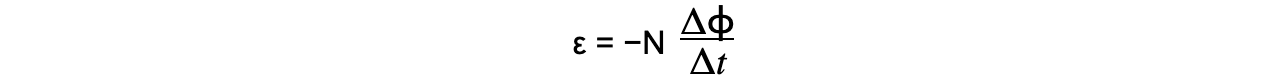
- This equation shows:
- When a bar magnet goes through a coil, an e.m.f is induced within the coil due to a change in magnetic flux
- A current is also induced which means the coil now has its own magnetic field
- The coil’s magnetic field acts in the opposite direction to the magnetic field of the bar magnet
- If a direct current (d.c) power supply is replaced with an alternating current (a.c) supply, the e.m.f induced will also be alternating with the same frequency as the supply
Experimental Evidence for Lenz’s Law
- To verify Lenz’s law, the only apparatus needed is:
- A bar magnet
- A coil of wire
- A sensitive ammeter
- Note: a cell is not required
- A known pole (either north or south) of the bar magnet is pushed into the coil, which induces a magnetic field in the coil
- Using the right hand grip rule, the curled fingers indicate the direction of the current and the thumb indicates the direction of the induced magnetic field
- The direction of the current is observed on the ammeter
- Reversing the magnet direction would give an opposite deflection on the meter
- The induced field (in the coil) repels the bar magnet
- This is because of Lenz’s law:
- The direction of the induced field in the coil pushes against the change creating it, ie. the bar magnet
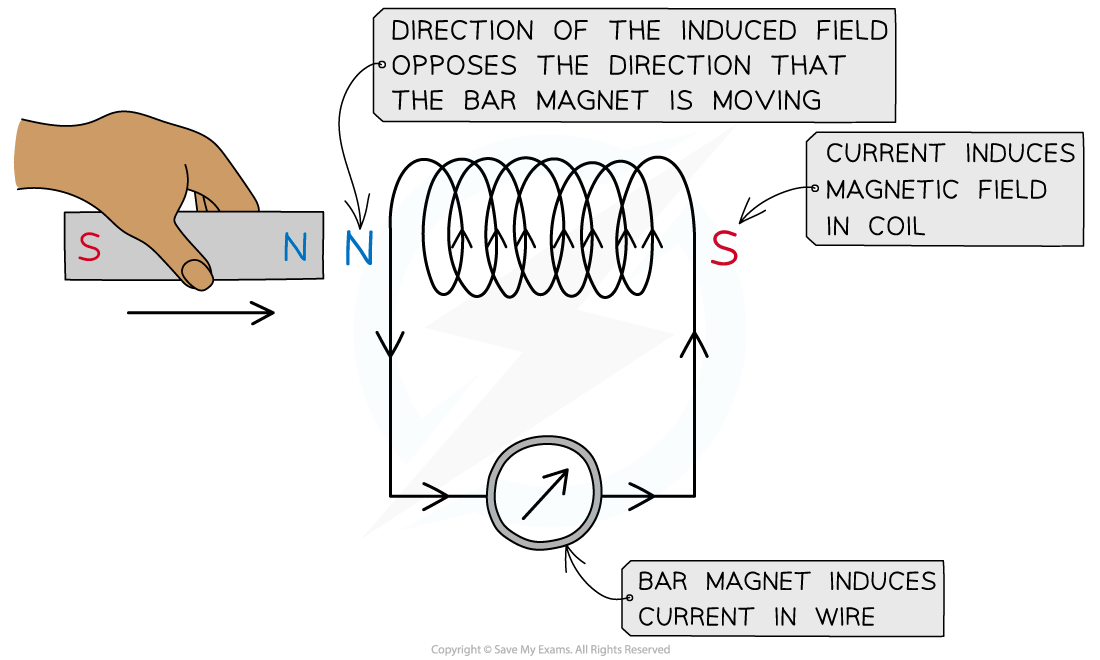
Lenz’s law can be verified using a coil connected in series with a sensitive ammeter and a bar magnet
Worked Example
A small rectangular coil contains 350 turns of wire. The longer sides are 3.5 cm and the shorter sides are 1.4 cm.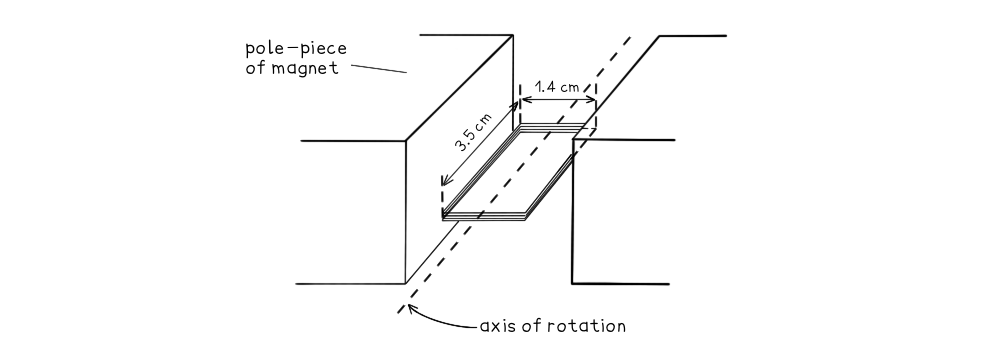
The coil is held between the poles of a large magnet so that the coil can rotate about an axis through its centre.The magnet produces a uniform magnetic field of flux density 80 mT between its poles. The coil is positioned horizontally and then turned through an angle of 40° in a time of 0.18 s.Calculate the magnitude of the average e.m.f induced in the coil.
Step 1: Write down the known quantities
Magnetic flux density, B = 80 mT = 80 × 10-3 T
Area, A = 3.5 × 1.4 = (3.5 × 10-2) × (1.4 × 10-2) = 4.9 × 10-4 m2
Number of turns, N = 350
Time interval, Δt = 0.18 s
Angle between coil and field lines, θ = 40o
Step 2: Write out the equation for Faraday’s law:
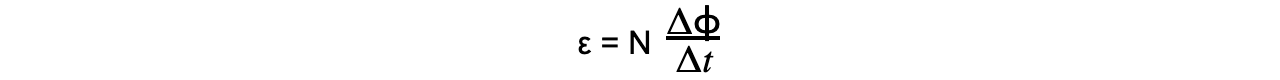
Step 3: Write out the equation for flux linkage:
ɸN = BAN cos(θ)
Step 4: Substitute values into flux linkage equation:
ɸN = (80 × 10-3) × (4.9 × 10-4) × 350 × cos(40) = 0.0105 Wb turns
Step 5: Substitute flux linkage and time into Faraday’s law equation:
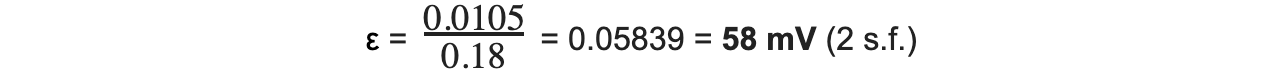
转载自savemyexams

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








