- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
CIE A Level Physics复习笔记19.2.2 Capacitor Discharge Equations
The Time Constant
- The time constant of a capacitor discharging through a resistor is a measure of how long it takes for the capacitor to discharge
- The definition of the time constant is:
The time taken for the charge of a capacitor to decrease to 0.37 of its original value
 The time constant gives an easy way to compare the rate of change of similar quantities eg. charge, current and p.d.
The time constant gives an easy way to compare the rate of change of similar quantities eg. charge, current and p.d.- The time constant is defined by the equation:
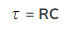 Where:
Where:
 R = resistance of the resistor (Ω)
R = resistance of the resistor (Ω)- C = capacitance of the capacitor (F)

The graph of voltage-time for a discharging capacitor showing the positions of the first three time constants
Worked Example
A capacitor of 7 nF is discharged through a resistor of resistance R. The time constant of the discharge is 5.6 × 10-3 s.Calculate the value of R.
Step 1: Write out the known quantities
Capacitance, C = 7 nF = 7 × 10-9 F
Time constant, τ = 5.6 × 10-3 s
Step 2: Write down the time constant equation
τ = RC
Step 3: Rearrange for resistance R
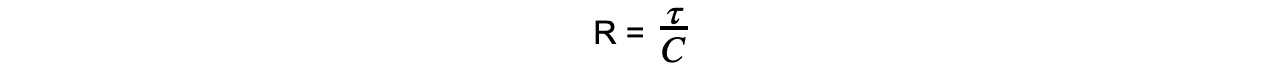
Step 4: Substitute in values and calculate
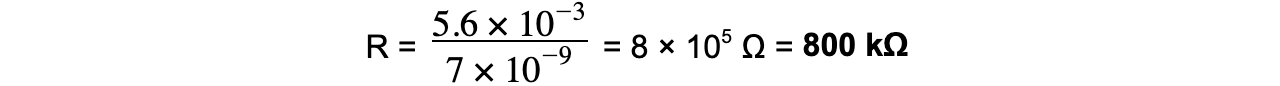
Using the Capacitor Discharge Equation
- The time constant is used in the exponential decay equations for the current, charge or potential difference (p.d) for a capacitor discharging through a resistor
- These can be used to determine the amount of current, charge or p.d left after a certain amount of time when a capacitor is discharging
- The exponential decay of current on a discharging capacitor is defined by the equation:
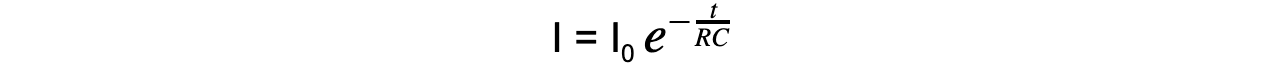
- Where:
- I = current (A)
- I0 = initial current before discharge (A)
- e = the exponential function
- t = time (s)
- RC = resistance (Ω) × capacitance (F) = the time constant τ (s)
- This equation shows that the faster the time constant τ, the quicker the exponential decay of the current when discharging
- Also, how big the initial current is affects the rate of discharge
- If I0 is large, the capacitor will take longer to discharge
- Note: during capacitor discharge, I0 is always larger than I, this is because the current I will always be decreasing
- The current at any time is directly proportional to the p.d across the capacitor and the charge across the parallel plates
- Therefore, this equation also describes the change in p.d and charge on the capacitor:
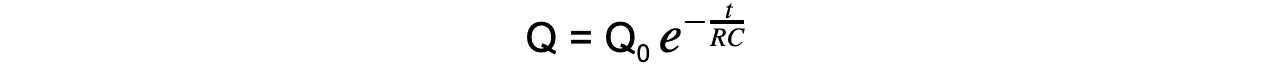
- Where:
- Q = charge on the capacitor plates (C)
- Q0 = initial charge on the capacitor plates (C)
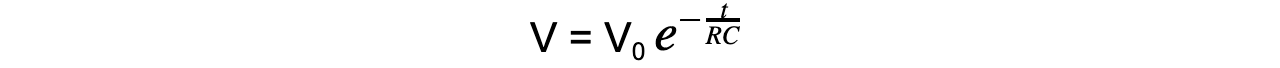
- Where:
- V = p.d across the capacitor (C)
- V0 = initial p.d across the capacitor (C)
The Exponential Function e
- The symbol e represents the exponential constant, a number which is approximately equal to e = 2.718...
- On a calculator it is shown by the button ex
- The inverse function of ex is ln(y), known as the natural logarithmic function
- This is because, if ex = y, then x = ln (y)
- The 0.37 in the definition of the time constant arises as a result of the exponential constant, the true definition is:


Worked Example
The initial current through a circuit with a capacitor of 620 μF is 0.6 A. The capacitor is connected across the terminals of a 450 Ω resistor.Calculate the time taken for the current to fall to 0.4 A.
Step 1: Write out the known quantities
Initial current before discharge, I0 = 0.6 A
Current, I = 0.4 A
Resistance, R = 450 Ω
Capacitance, C = 620 μF = 620 × 10-6 F
Step 2: Write down the equation for the exponential decay of current
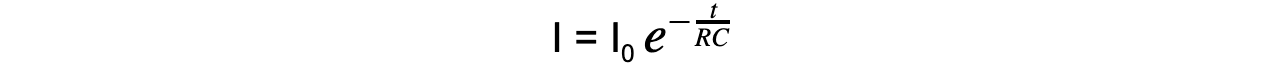
Step 3: Calculate the time constant
τ = RC
τ = 450 × (620 × 10-6) = 0.279 s
Step 4: Substitute into the current equation
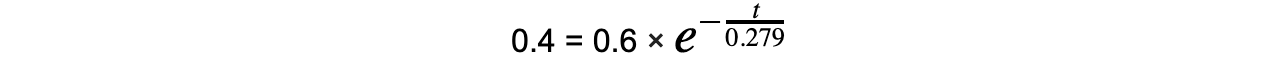
Step 5: Rearrange for the time t
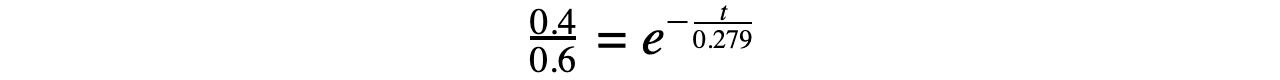
The exponential can be removed by taking the natural log of both sides:
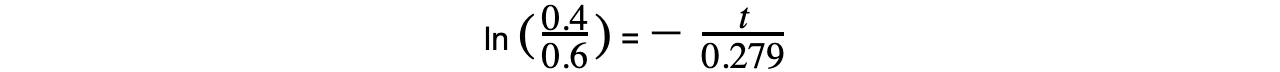
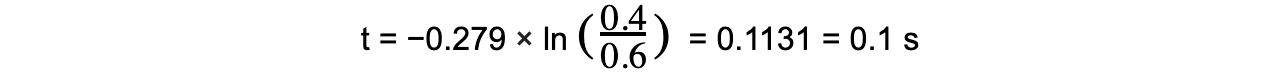
Exam Tip
Make sure you’re confident in rearranging equations with natural logs (ln) and the exponential function (e). To refresh your knowledge of this, have a look at the AS Maths revision notes on Exponentials & Logarithms
转载自savemyexams

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









