CIE A Level Physics复习笔记17.1.6 Energy in SHM

• During simple harmonic motion, energy is constantly exchanged between two forms: kinetic and potential
• The potential energy could be in the form of:
  • Gravitational potential energy (for a pendulum)
  • Elastic potential energy (for a horizontal mass on a spring)
  • Or both (for a vertical mass on a spring)
• Speed, v, is at a maximum when displacement, x, = 0, so:

The system has maximum kinetic energy when the displacement is zero because the oscillator is at its equilibrium position and so moving at maximum velocity.

• Therefore, the kinetic energy is zero at maximum displacement x = x₀, so:

• A simple harmonic system is therefore constantly converting between kinetic and potential energy
  • When one increases, the other decreases and vice versa, therefore:

The total energy of a simple harmonic system always remains constant and is equal to the sum of the kinetic and potential energies

The kinetic and potential energy of an oscillator in SHM vary periodically

• The key features of the energy-time graph are:
  • Both the kinetic and potential energies are represented by periodic functions (sine or cosine) which are varying in opposite directions to one another
  • When the potential energy is 0, the kinetic energy is at its maximum point and vice versa
  • The total energy is represented by a horizontal straight line directly above the curves at the maximum value of both the kinetic or potential energy
  • Energy is always positive so there are no negative values on the y axis
• Recall that the kinetic energy is defined by the equation

• Gravitational potential energy is defined by the equation

• Note: kinetic and potential energy go through two complete cycles during one period of oscillation
  • This is because one complete oscillation reaches the maximum displacement twice (positive and negative)
• The energy-displacement graph for half a cycle looks like:

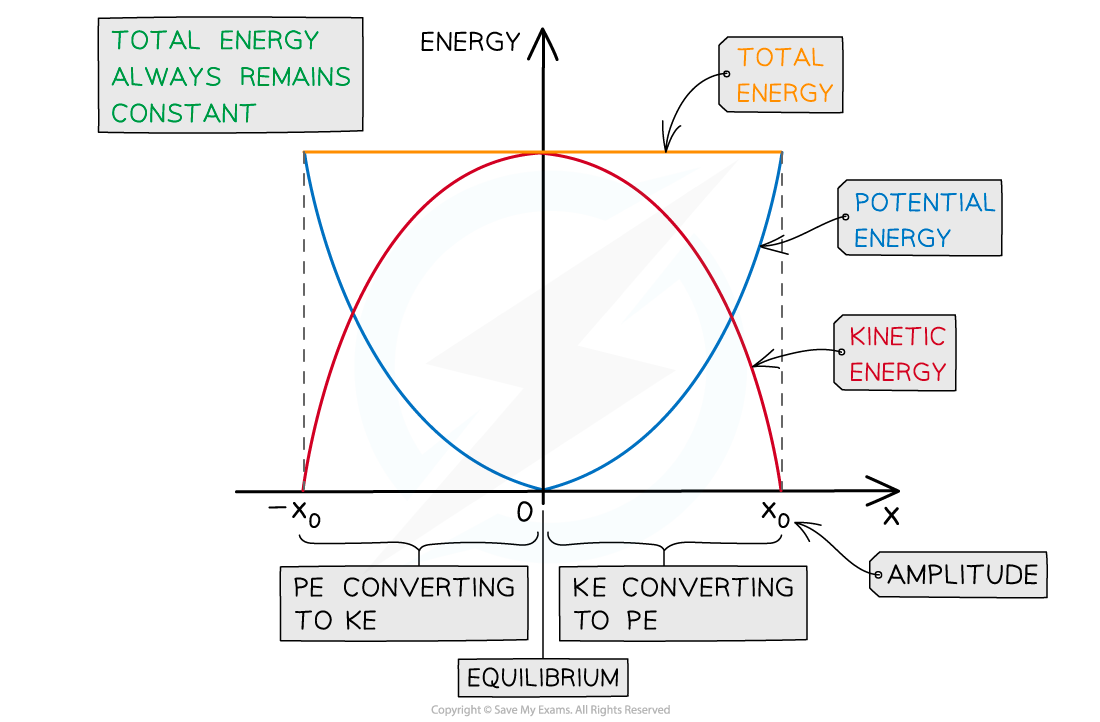
Potential and kinetic energy v displacement in half a period of an SHM oscillation

• The key features of the energy-displacement graph:
  • Displacement is a vector, so, the graph has both positive and negative x values
  • The potential energy is always at a maximum at the amplitude positions x₀ and 0 at the equilibrium position (x = 0)
  • This is represented by a ‘U’ shaped curve
  • The kinetic energy is the opposite: it is 0 at the amplitude positions x₀ and maximum at the equilibrium position x = 0
  • This is represented by a ‘n’ shaped curve
  • The total energy is represented by a horizontal straight line above the curves

The total energy of system undergoing simple harmonic motion is defined by:

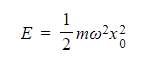
• Where:
  • E = total energy of a simple harmonic system (J)
  • m = mass of the oscillator (kg)
  • ⍵ = angular frequency (rad s^-1)
  • x₀ = amplitude (m)

Step 1: Write down all known quantities

Mass, m = 23 g = 23 × 10^–3 kg

Amplitude, x₀ = 1.5 cm = 0.015 m

Frequency, f = 4.8 Hz

Step 2: Write down the equation for the total energy of SHM oscillations: