- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
CIE A Level Physics复习笔记13.2.1 Gravitational Potential
Gravitational Potential
- The gravitational potential energy (G.P.E) is the energy an object has when lifted off the ground given by the familiar equation:
G.P.E = mgΔh
- The G.P.E on the surface of the Earth is taken to be 0
- This means work is done to lift the object
- However, outside the Earth’s surface, G.P.E can be defined as:
The energy an object possess due to its position in a gravitational field
- The gravitational potential at a point is the gravitational potential energy per unit mass at that point
- Therefore, the gravitational potential is defined as:
The work done per unit mass in bringing a test mass from infinity to a defined point
Calculating Gravitational Potential
- The equation for gravitational potential ɸ is defined by the mass M and distance r:
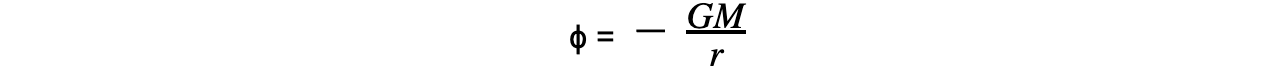
- Where:
- ɸ = gravitational potential (J kg-1)
- G = Newton’s gravitational constant
- M = mass of the body producing the gravitational field (kg)
- r = distance from the centre of the mass to the point mass (m)
- The gravitational potential is negative near an isolated mass, such as a planet, because the potential when r is at infinity is defined as 0
- Gravitational forces are always attractive so as r decreases, positive work is done by the mass when moving from infinity to that point
- When a mass is closer to a planet, its gravitational potential becomes smaller (more negative)
- As a mass moves away from a planet, its gravitational potential becomes larger (less negative) until it reaches 0 at infinity
- This means when the distance (r) becomes very large, the gravitational force tends rapidly towards 0 at a point further away from a planet
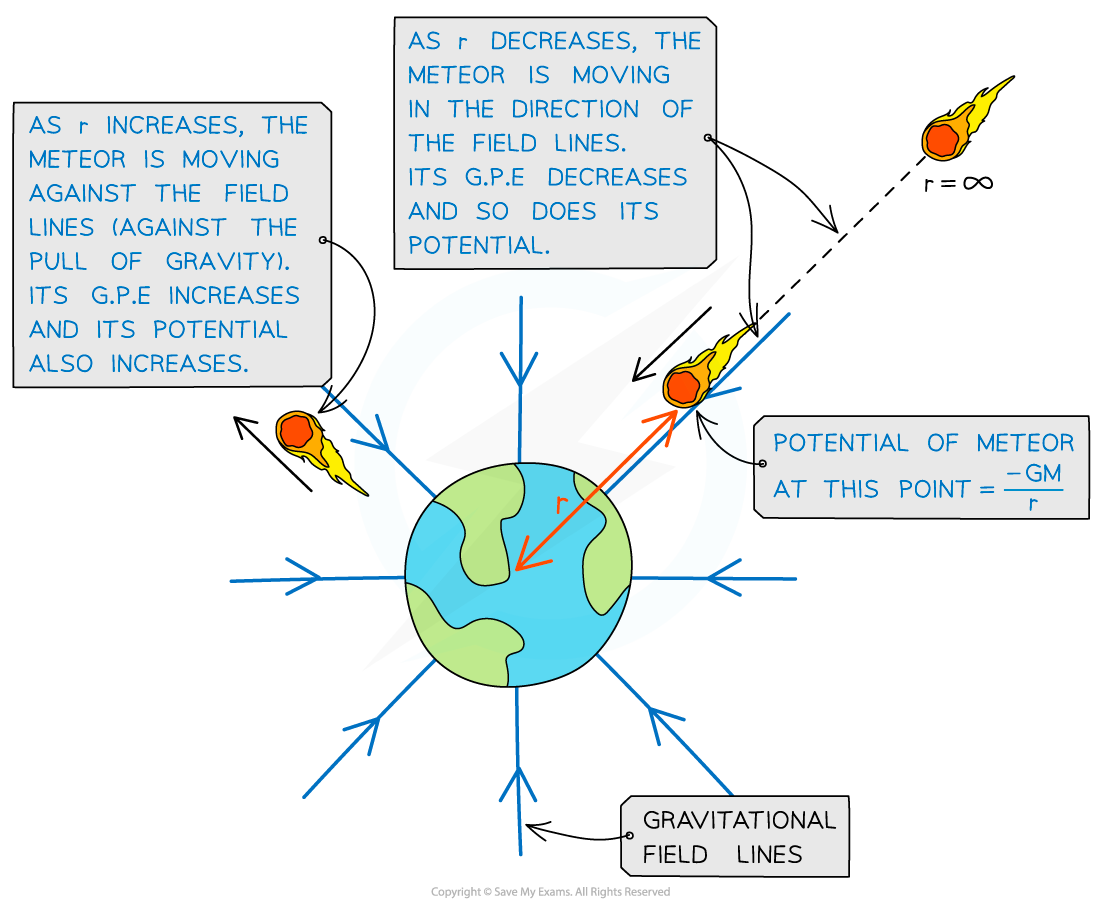
Gravitational potential increases and decreases depending on whether the object is travelling towards or against the field lines from infinity
Worked Example
A planet has a diameter of 7600 km and a mass of 3.5 × 1023 kg. A rock of mass 528 kg accelerates towards the planet from infinity.At a distance of 400 km above the planet’s surface, calculate the gravitational potential of the rock.
Step 1: Write the gravitational potential equation
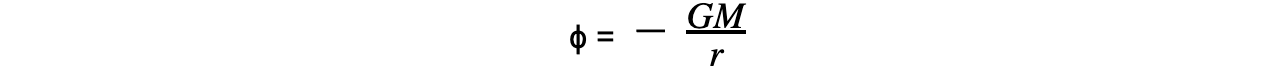
Step 2: Determine the value of r
r is the distance from the centre of the planet
Radius of the planet = planet diameter ÷ 2 = 7600 ÷ 2 = 3800 km
r = 3800 + 400 = 4200 km = 4.2 × 106 m
Step 3: Substitute in values
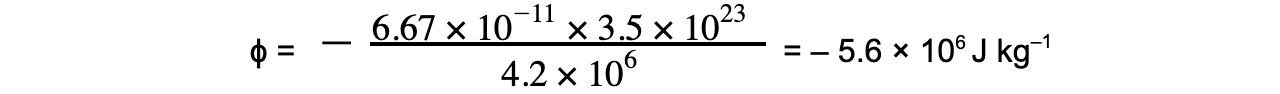
Exam Tip
Remember to keep the negative sign in your solution for gravitational potential. However, if you’re asked for the ‘change in’ gravitational potential, no negative sign should be included since you are finding a difference in values (between 0 at infinity and the gravitational potential from your calculation).
转载自savemyexams

最新发布
© 2026. All Rights Reserved. 沪ICP备2023009024号-1









