- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
CIE A Level Physics复习笔记13.1.5 Gravitational Field Strength
Deriving Gravitational Field Strength (g)
- The gravitational field strength at a point describes how strong or weak a gravitational field is at that point
- The gravitational field strength due to a point mass can be derived from combining the equations for Newton’s law of gravitation and gravitational field strength
- For calculations involving gravitational forces, a spherical mass can be treated as a point mass at the centre of the sphere
- Newton’s law of gravitation states that the attractive force F between two masses M and m with separation r is equal to:

- The gravitational field strength at a point is defined as the force F per unit mass m

- Substituting the force F with the gravitational force FG leads to:

- Cancelling mass m, the equation becomes:
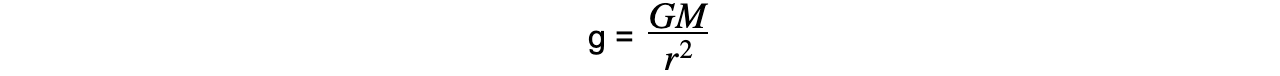
- Where:
- g = gravitational field strength (N kg-1)
- G = Newton’s Gravitational Constant
- M = mass of the body producing the gravitational field (kg)
- r = distance from the mass where you are calculating the field strength (m)
Calculating g
- Gravitational field strength, g, is a vector quantity
- The direction of g is always towards the centre of the body creating the gravitational field
- This is the same direction as the gravitational field lines
- On the Earth’s surface, g has a constant value of 9.81 N kg-1
- However outside the Earth’s surface, g is not constant
- g decreases as r increases by a factor of 1/r2
- This is an inverse square law relationship with distance
- When g is plotted against the distance from the centre of a planet, r has two parts:
- When r < R, the radius of the planet, g is directly proportional to r
- When r > R, g is inversely proportional to r2(this is an ‘L’ shaped curve and shows that g decreases rapidly with increasing distance r)

 Graph showing how gravitational field strength varies at greater distance from the Earth’s surface
Graph showing how gravitational field strength varies at greater distance from the Earth’s surface- Sometimes, g is referred to as the ‘acceleration due to gravity’ with units of m s-2
- Any object that falls freely in a uniform gravitational field on Earth has an acceleration of 9.81 m s-2
Worked Example
The mean density of the moon is ⅗ times the mean density of the Earth. The gravitational field strength is ⅙ on the Moon than that on Earth.Determine the ratio of the Moon’s radius rM and the Earth’s radius rE.
Step 1: Write down the known quantities 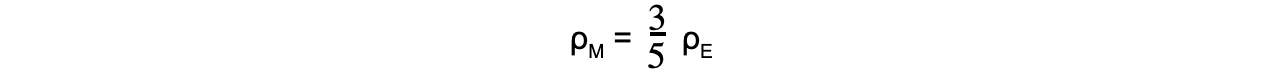
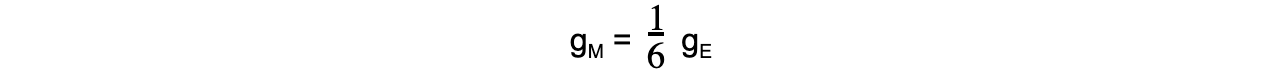 gM = gravitational field strength on the Moon, ρM = mean density of the Moon
gM = gravitational field strength on the Moon, ρM = mean density of the Moon
gE = gravitational field strength on the Earth, ρE = mean density of the Earth Step 2: The volumes of the Earth and Moon are equal to the volume of a sphere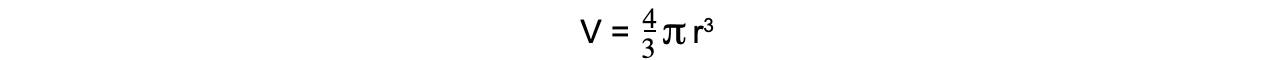 Step 3: Write the density equation and rearrange for mass M
Step 3: Write the density equation and rearrange for mass M 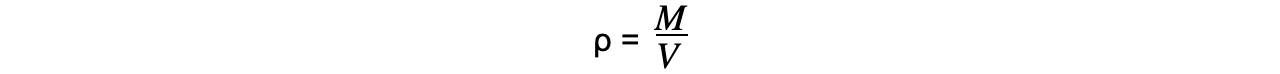 M = ρV
M = ρV
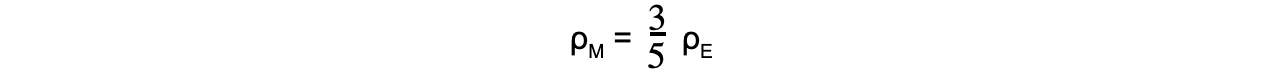
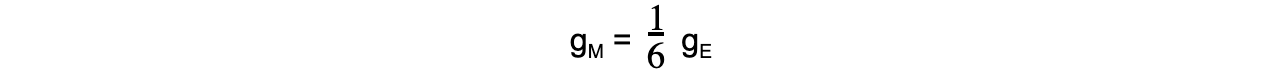 gM = gravitational field strength on the Moon, ρM = mean density of the Moon
gM = gravitational field strength on the Moon, ρM = mean density of the MoongE = gravitational field strength on the Earth, ρE = mean density of the Earth Step 2: The volumes of the Earth and Moon are equal to the volume of a sphere
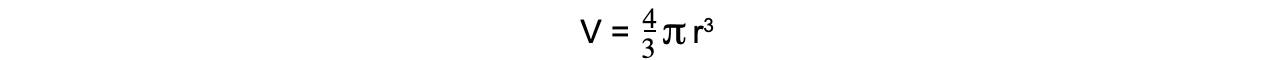 Step 3: Write the density equation and rearrange for mass M
Step 3: Write the density equation and rearrange for mass M 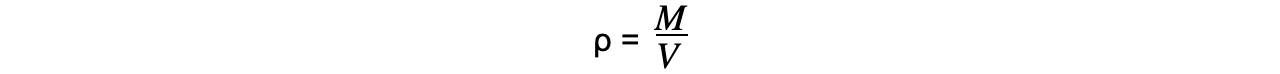 M = ρV
M = ρVStep 4: Write the gravitational field strength equation 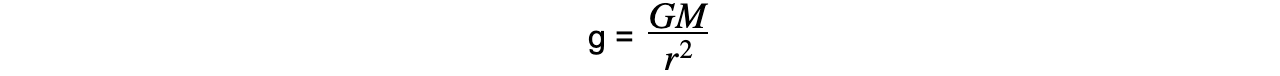 Step 5: Substitute M in terms of ρ and V
Step 5: Substitute M in terms of ρ and V 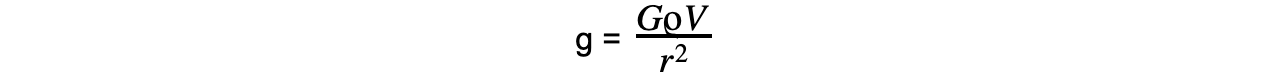 Step 6: Substitute the volume of a sphere equation for V, and simplify
Step 6: Substitute the volume of a sphere equation for V, and simplify 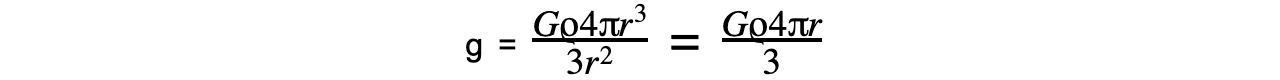
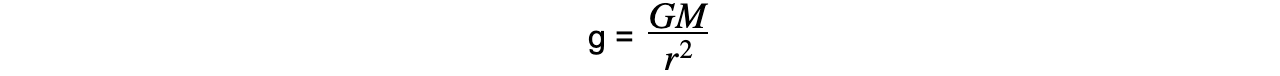 Step 5: Substitute M in terms of ρ and V
Step 5: Substitute M in terms of ρ and V 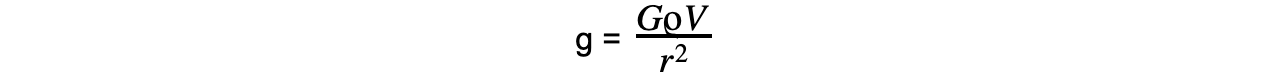 Step 6: Substitute the volume of a sphere equation for V, and simplify
Step 6: Substitute the volume of a sphere equation for V, and simplify 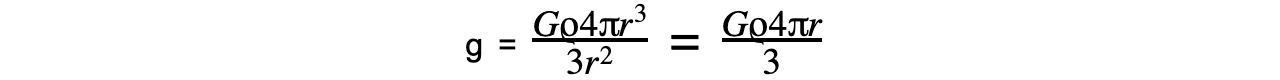
Step 7: Find the ratio of the gravitational field strengths 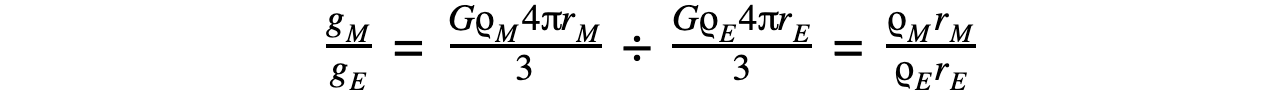 Step 8: Rearrange and calculate the ratio of the Moon’s radius rM and the Earth’s radius rE
Step 8: Rearrange and calculate the ratio of the Moon’s radius rM and the Earth’s radius rE 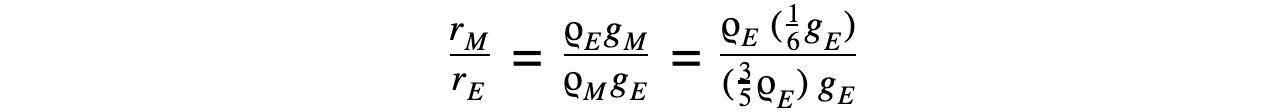
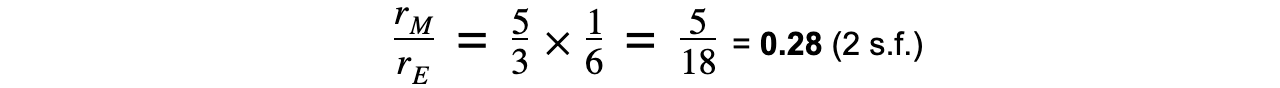
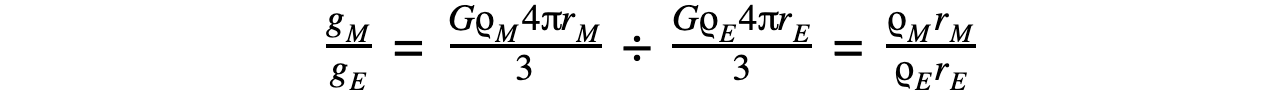 Step 8: Rearrange and calculate the ratio of the Moon’s radius rM and the Earth’s radius rE
Step 8: Rearrange and calculate the ratio of the Moon’s radius rM and the Earth’s radius rE 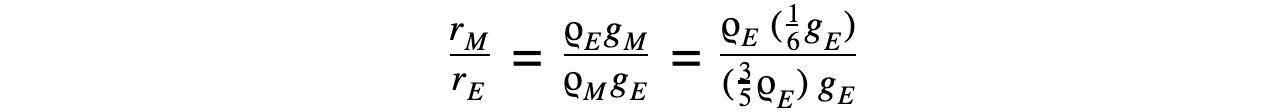
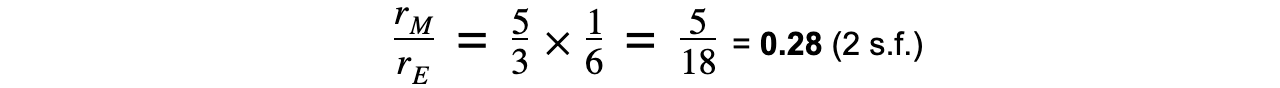
转载自savemyexams


最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








