CIE A Level Chemistry复习笔记5.1.4 Calculations using Born-Haber Cycles

• Once a Born-Haber cycle has been constructed, it is possible to calculate the lattice energy (ΔHlattꝋ) by applying Hess’s law and rearranging:

ΔH_f^ꝋ = ΔH_at^ꝋ + ΔH_at^ꝋ + IE + EA + ΔH_latt^ꝋ

• If we simplify this into three terms, this makes the equation easier to see:
  • ΔH_latt^ꝋ
  • ΔH_f^ꝋ
  • ΔH₁^ꝋ (the sum of all of the various enthalpy changes necessary to convert the elements in their standard states to gaseous ions)
• The simplified equation becomes

ΔH_fꝋ = ΔH₁ꝋ + ΔH_lattꝋ

So, if we rearrange to calculate the lattice energy, the equation becomesΔH_latt^ꝋ = ΔH_f^ꝋ - ΔH₁^ꝋ

• When calculating the ΔHlattꝋ, all other necessary values will be given in the question
• A Born-Haber cycle could be used to calculate any stage in the cycle
  • For example, you could be given the lattice energy and asked to calculate the enthalpy change of formation of the ionic compound
  • The principle would be exactly the same
  • Work out the direct and indirect route of the cycle (the stage that you are being asked to calculate will always be the direct route)
  • Write out the equation in terms of enthalpy changes and rearrange if necessary to calculate the required value
• Remember: sometimes a value may need to be doubled or halved, depending on the ionic solid involved
  • For example, with MgCl₂ the value for the first electron affinity of chlorine would need to be doubled in the calculation, because there are two moles of chlorine atoms
  • Therefore, you are adding 2 moles of electrons to 2 moles of chlorine atoms, to form 2 moles of Cl^- ions

Worked example: Calculating the lattice energy of KCl

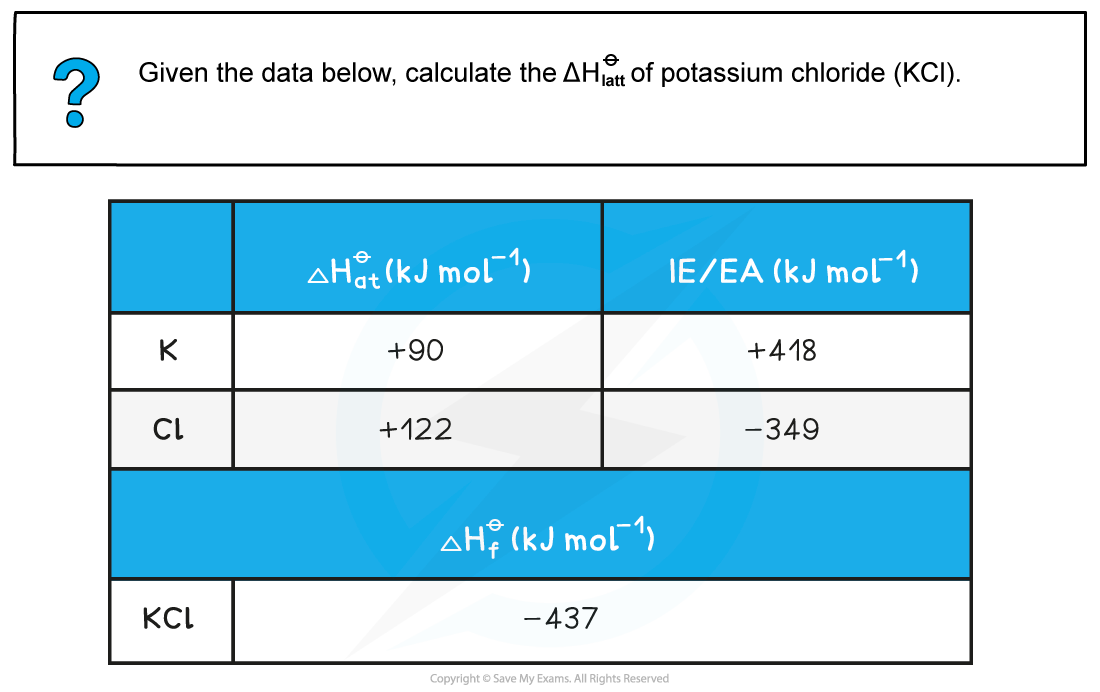
Answer

• Step 1: The corresponding Born-Haber cycle is:

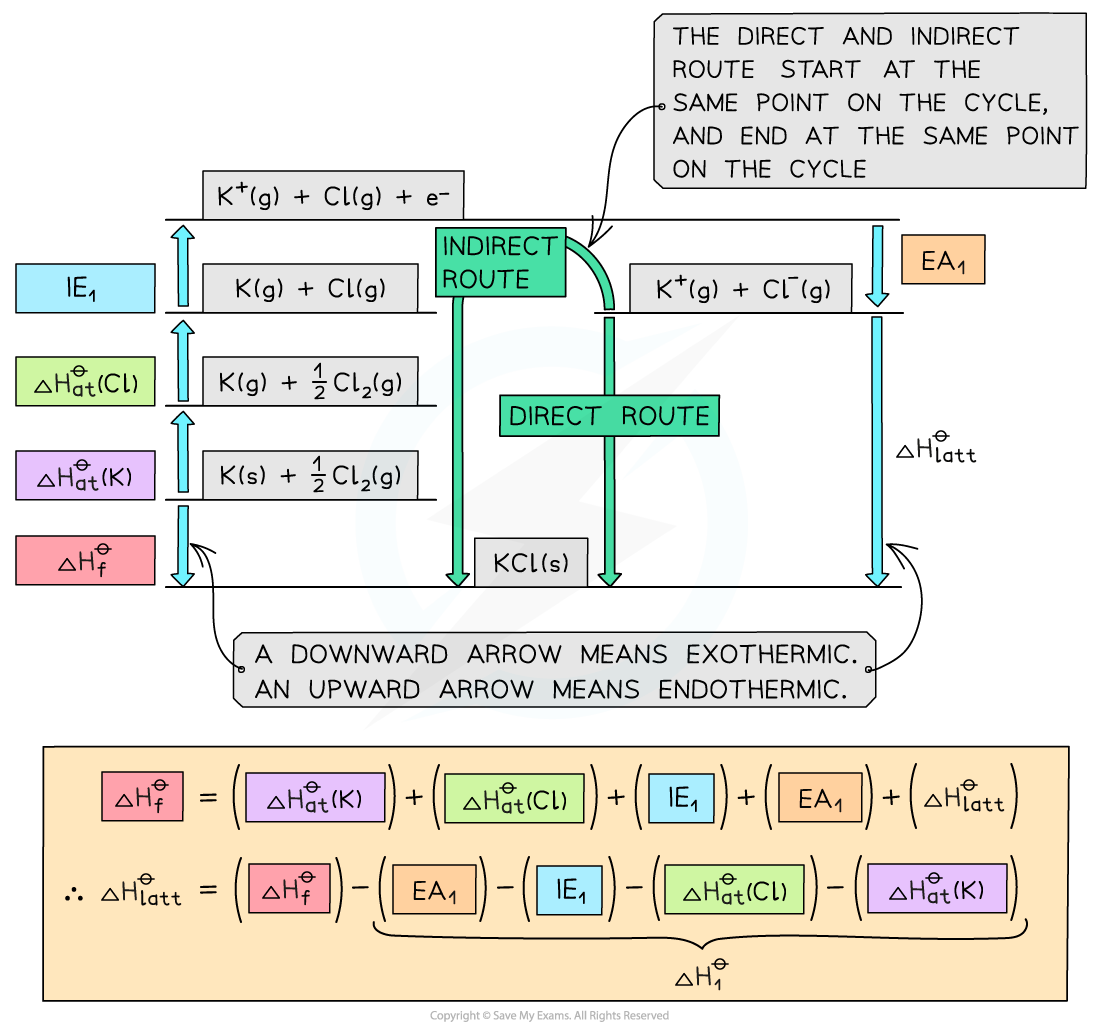
• Step 2: Applying Hess’ law, the lattice energy of KCl is:

ΔH_latt^ꝋ = ΔH_f^ꝋ - ΔH₁^ꝋ

ΔH_latt^ꝋ = ΔH_f^ꝋ - [(ΔH_at^ꝋ K) + (ΔH_at^ꝋ Cl) + (IE₁ K) + (EA₁ Cl)]

• Step 3: Substitute in the numbers:

ΔH_latt^ꝋ = (-437) - [(+90) + (+122) + (+418) + (-349)] = -718 kJ mol^-1

Worked example: Calculating the lattice energy of MgO

Answer

• Step 1: The corresponding Born-Haber cycle is:

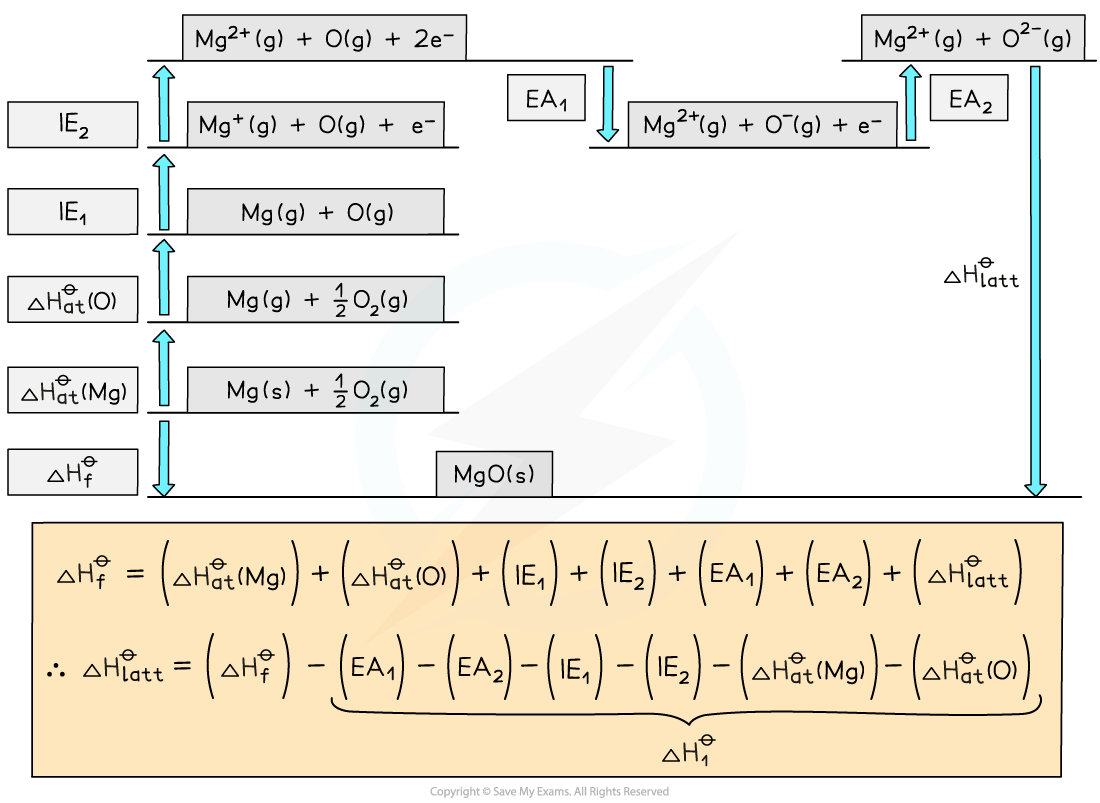
• Step 2: Applying Hess’ law, the lattice energy of MgO is:

ΔH_latt^ꝋ = ΔH_f^ꝋ - ΔH₁^ꝋ

ΔH_latt^ꝋ = ΔH_f^ꝋ - [(ΔH_at^ꝋ Mg) + (ΔH_at^ꝋ O) + (IE₁ Mg) + (IE₂ Mg) + (EA₁ O) + (EA₂ O)]

• Step 3: Substitute in the numbers:

ΔH_latt^ꝋ = (-602) - [(+148) + (+248) + (+736) + (+1450) + (-142) + (+770)]= -3812 kJ mol^-1