CIE A Level Biology复习笔记17.1.4 Variation: t-test Worked Example

Solution

• • Null hypothesis: There is no significant difference between the ear lengths of the rabbits in populations A and B
  • Sample sizes:
    • Population A: n1 = 15
    • Population B: n2 = 15

Step 1: Calculate the mean for each data set:

Mean for population A  x̅1 = 885 / 15 = 59 mm

Mean for population B  x̅2 = 870 / 15 = 58 mm

Step 2: Calculate the standard deviation (s) for each set of data

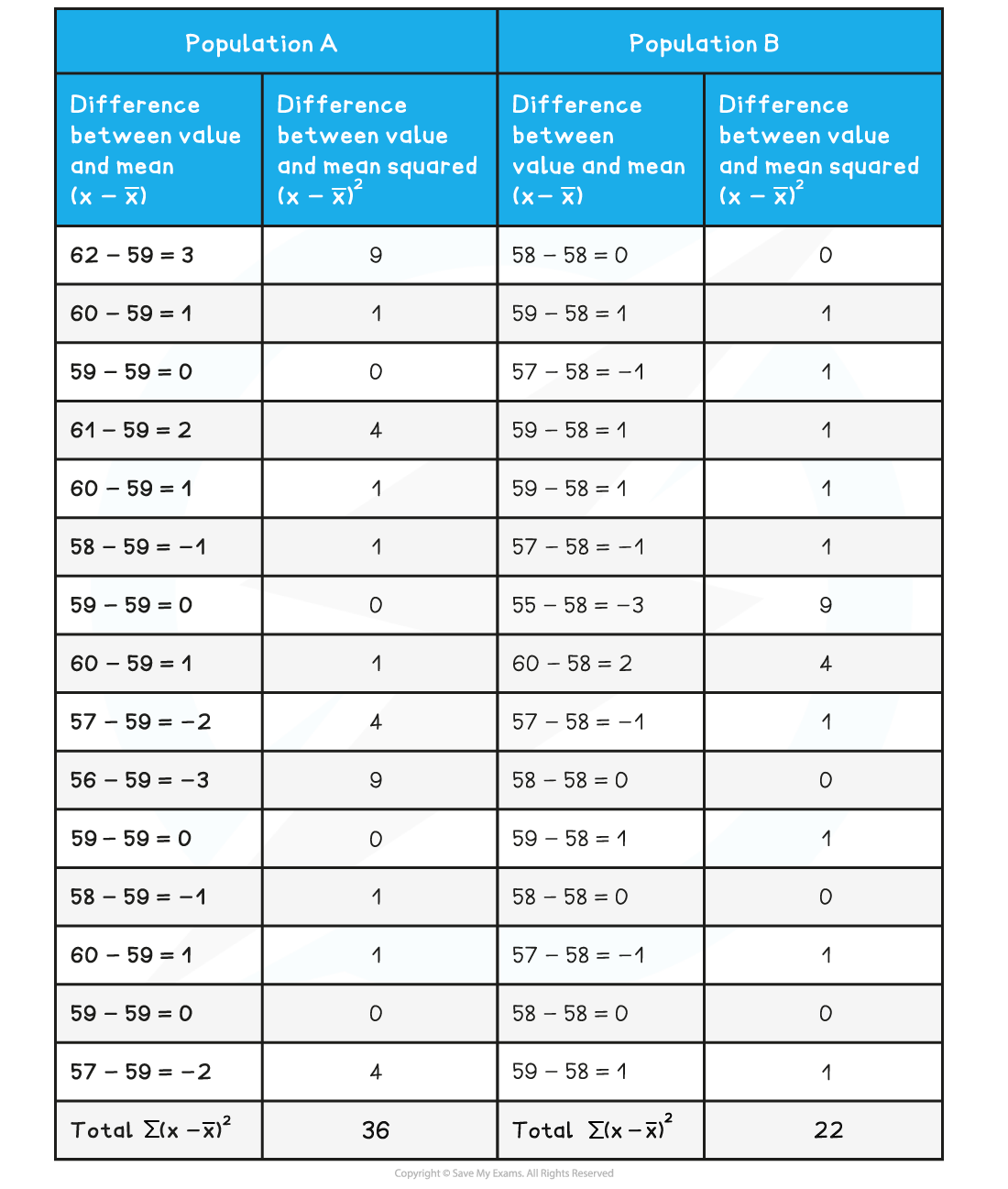
To find the standard deviations divide the sum of each square by n - 1 for each data set, and take the square root of each value

Step 3: Square the standard deviation and divide by n (the number of observations) in each sample, for both samples:

Step 4: Add the values from step 3 together and find the square root

Step 5: Divide the difference between the two means by the value from step 4

Step 6: Calculate the degrees of freedom (v) for all the data:

v = (n₁ - 1) + (n₂ - 1) = 14 + 14 = 28

Step 7: Look at a table that relates t values to the probability that the differences between data sets is due to chance to find where the t value of 1.91 for 28 degrees of freedom (v) calculated lies

Step 8: Draw a conclusion about the statistical relevance of the data

A t value of 1.91 represents a probability between 0.05 and 0.1 which is greater than the critical value of 0.05.

This means the null hypothesis should be accepted, as there are no significant differences between the two sets of results (any differences between the means of the ear length of rabbits in the two populations are due to chance)