AQA A Level Maths: Pure复习笔记8.2.3 Reverse Chain Rule
Reverse Chain Rule
What is the chain rule?
- The Chain Rule is a way of differentiating two (or more) functions
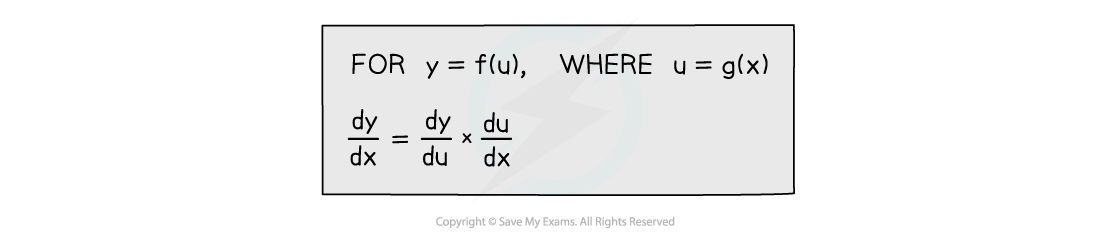
- In many simple cases the above formula/substitution is not needed
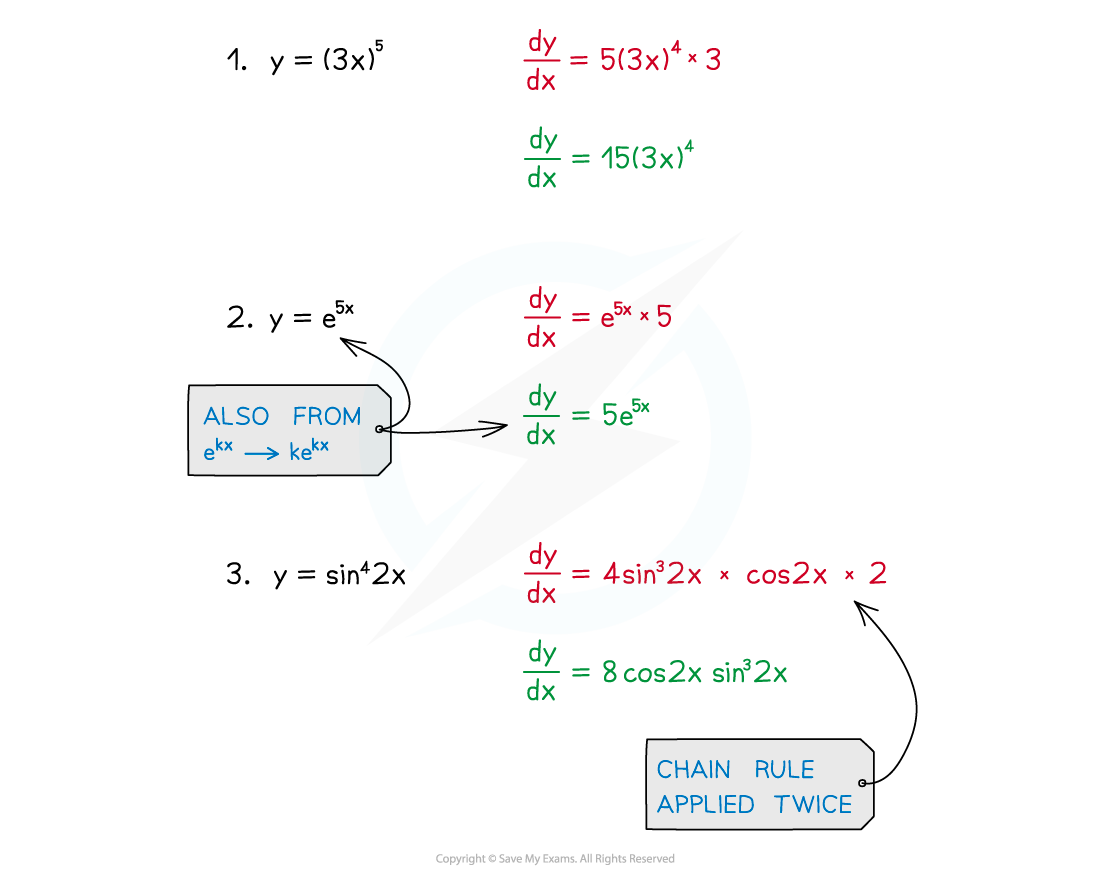
- The same can apply for the reverse – integration
Integrating with reverse chain rule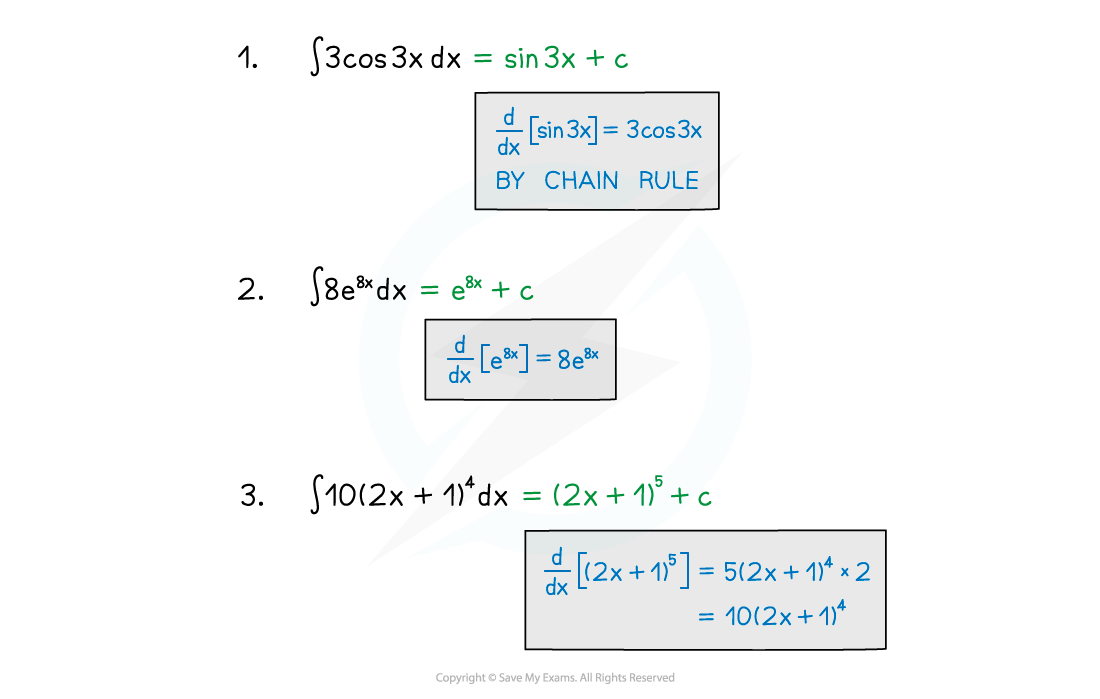
- In more awkward cases it can help to write the numbers in before integrating
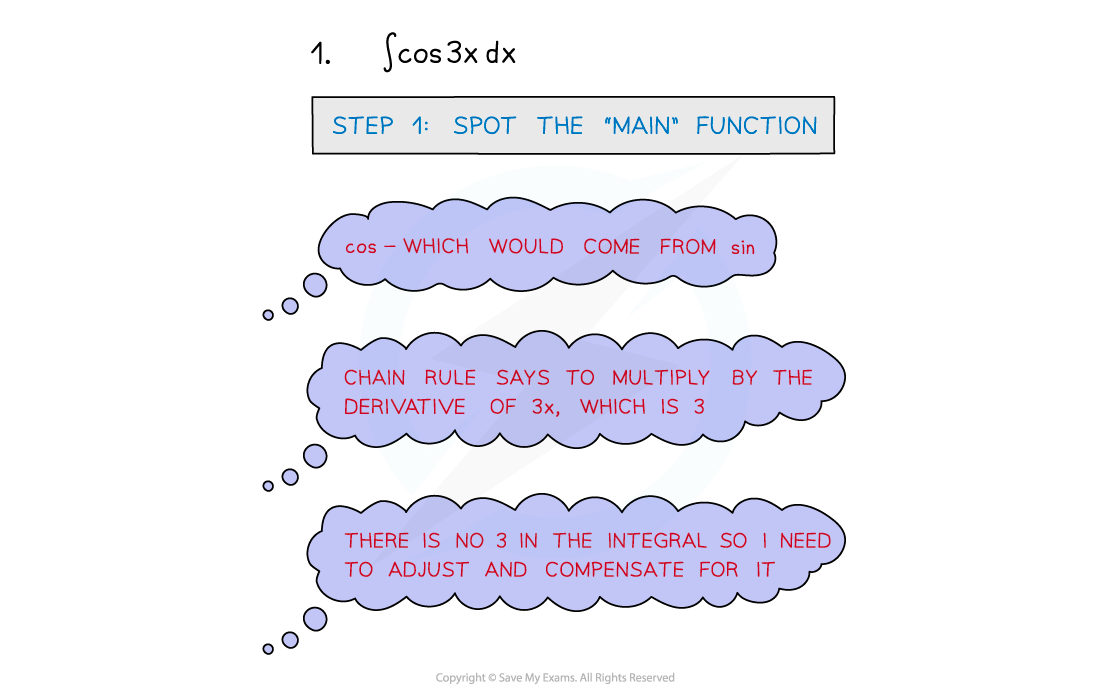
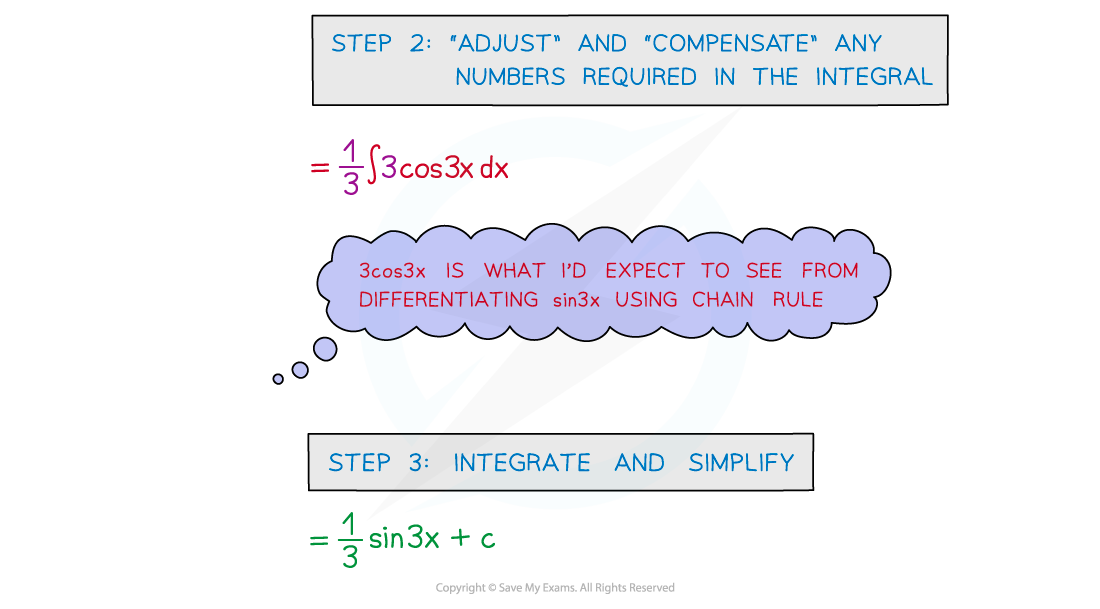
- STEP 1: Spot the ‘main’ function
- STEP 2: ‘Adjust’ and ‘compensate’ any numbers/constants required in the integral
- STEP 3: Integrate and simplify
Exam Tip
- If in doubt you can always use a substitution.
- Differentiation is easier than integration so if stuck try the opposite, eg. sin and cos are linked (remember that minus!) so if integrating a sin function, start by differentiating the corresponding cos function.
- Lastly, check your final answer by differentiating it.
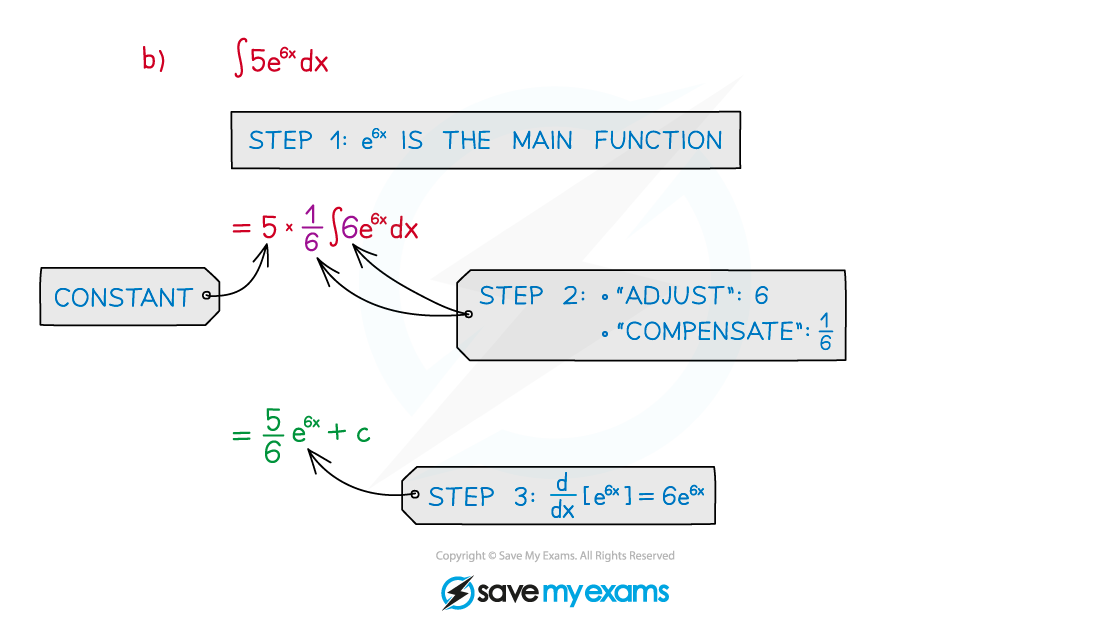
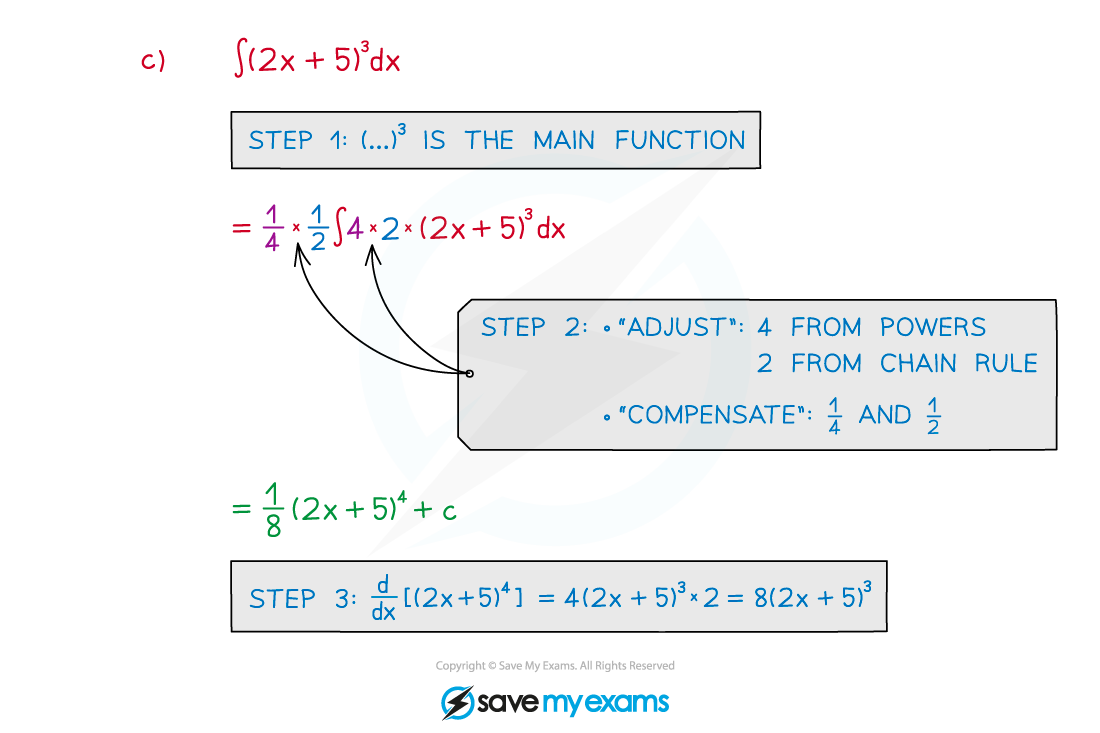
Worked Example
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
AMC8备考管家服务全新上线！
