- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
AQA A Level Maths: Pure复习笔记7.3.1 First Principles Differentiation - Trigonometry
First Principles Differentiation - Trigonometry
How do I derive the derivatives of trigonometric functions from first principles?
- Recall that for a function f(x) the definition of the derivative from first principles (see First Principles Differentiation) is:
 The small angle approximations allow us to produce the following intermediate limit results:
The small angle approximations allow us to produce the following intermediate limit results:
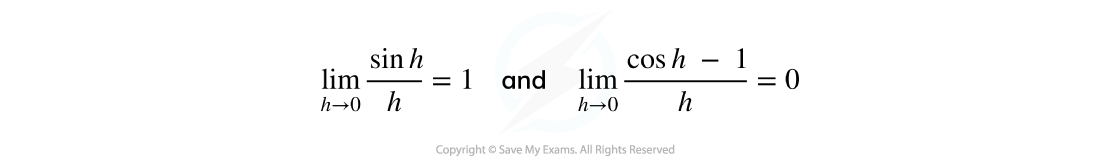
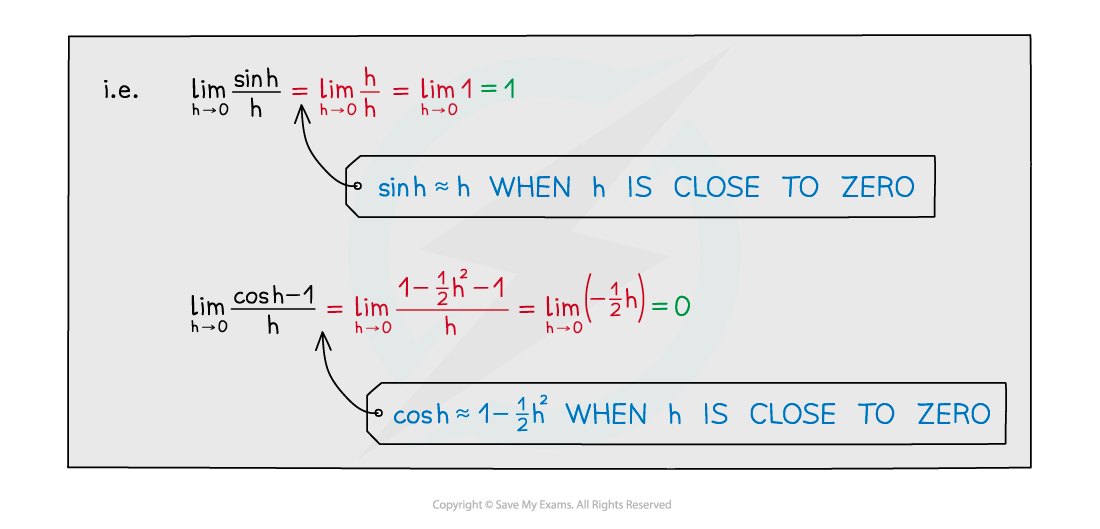
- And those intermediate results allow us to find the derivatives of sin and cos

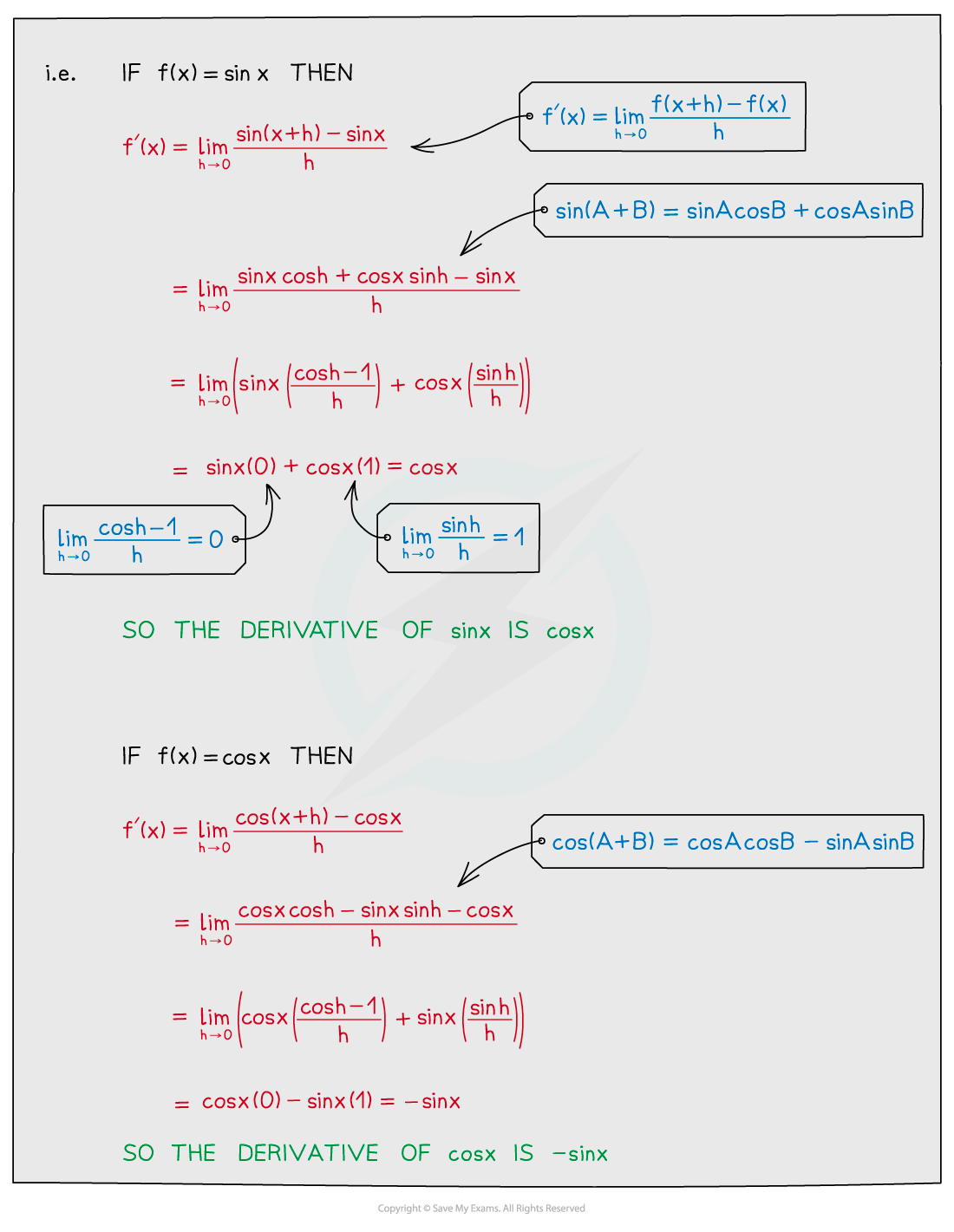
Derivatives of other trigonometric functions
- The derivative of tan is given by the following formula:

- The easiest way to derive this is to use the quotient rule and the derivatives of sin and cos
- But it can also be derived from first principles using the small angle approximation for tan (see the Worked Example)
- The general formulae for the derivatives of the trigonometric functions are:

- These formulae follow from combining the derivatives of the three basic functions with the chain rule, but they are worth knowing on their own
Exam Tip
- Remember that when doing calculus with trigonometric functions you have to measure angles in radians.
- The formula for the derivative of tan x is included in the exam formulae booklet.
- The derivatives of sin x and cos x are NOT included in the formula booklet – you have to know them.
- The small angle approximations for cos x, sin x and tan x are included in the exam formulae booklet – you don't have to memorise them.
- Be sure to read first principle differentiation exam questions clearly – they will state any results you can treat as 'givens' in your answer.
Worked Example
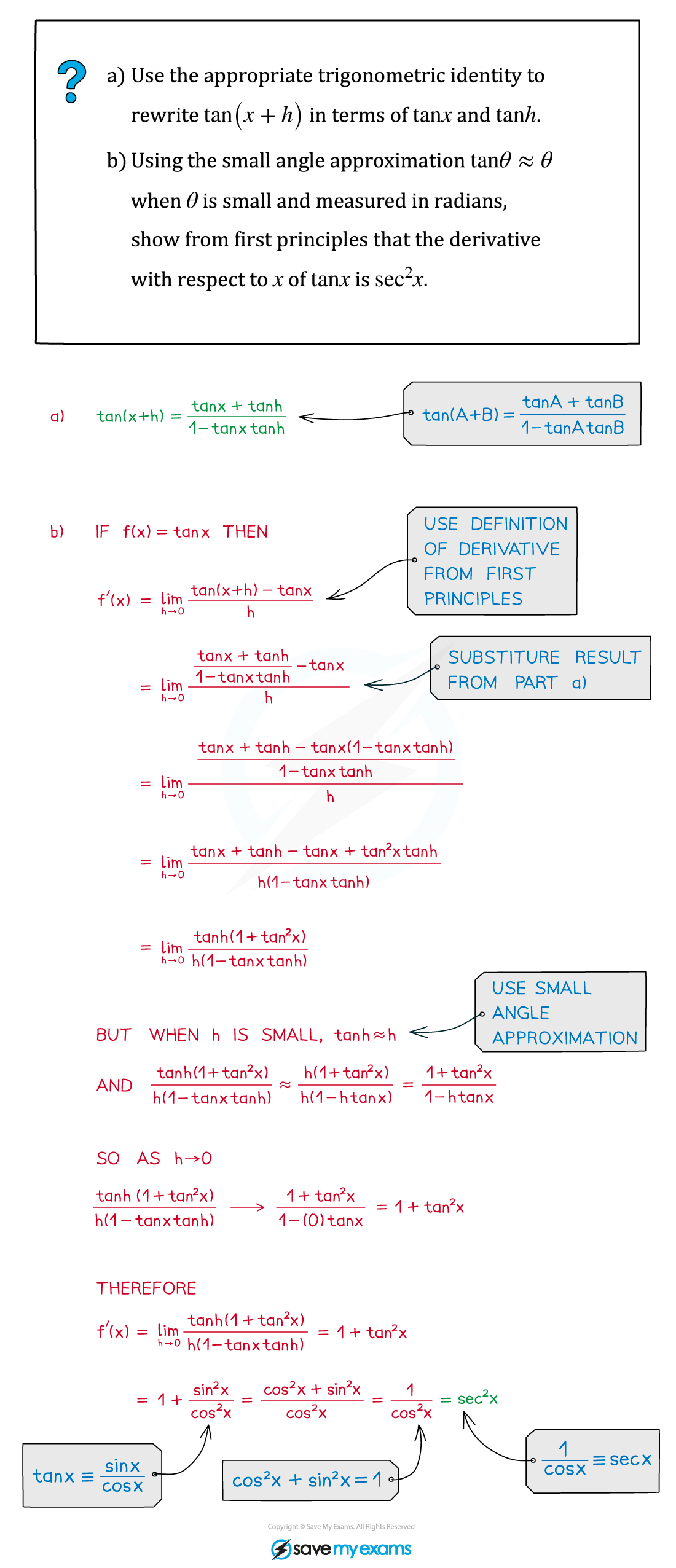
转载自savemyexams

在线登记
最新发布
翰林课程体验,退费流程快速投诉邮箱: yuxi@linstitute.net 沪ICP备2023009024号-1








