- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
AQA A Level Maths: Pure复习笔记6.3.3 Using Log Graphs in Modelling
Using Log Graphs in Modelling
What are log graphs?
- Log graphs are used when the scale of a graph increases or decreases exponentially
- It can very difficult to read specific values from graphs with these scales
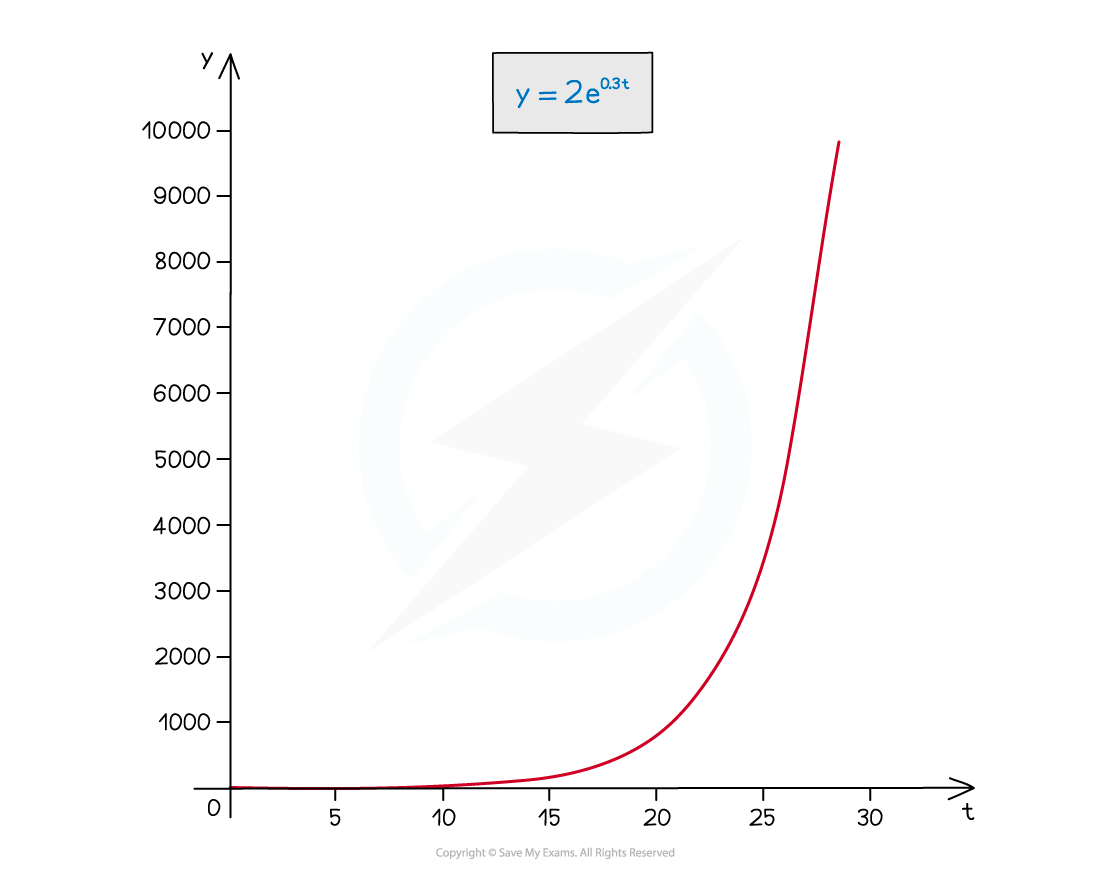
- Taking ln of both sides allows the equation to be rearranged into the form “y = mx + c”
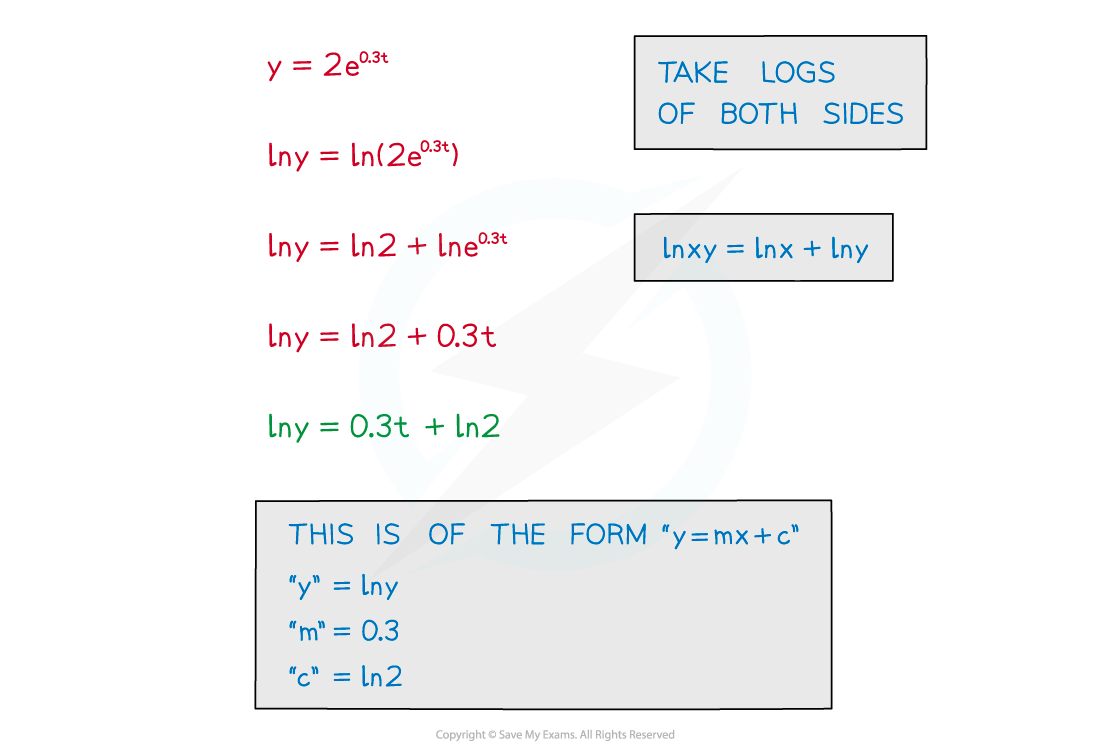
- Plotting ln y against t produces a straight line
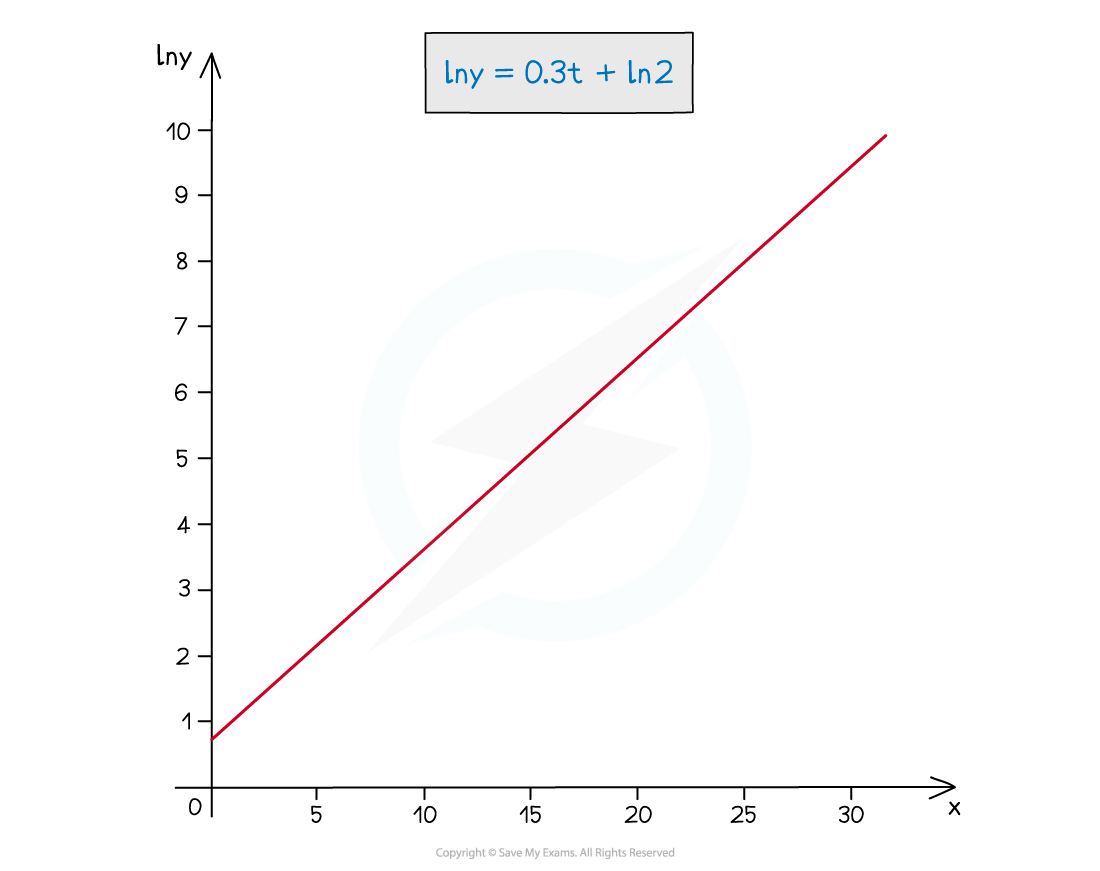
- Note the second graph has ln y on the y-axis
- Log graphs have at least one logarithmic axis
- Reading a value for ln y at t = 20 is easier than reading the value for y
- Logarithmic axes are used where a wide range of numbers can occur
- it makes numbers smaller and easier to deal with
- a curve can be turned into a straight line
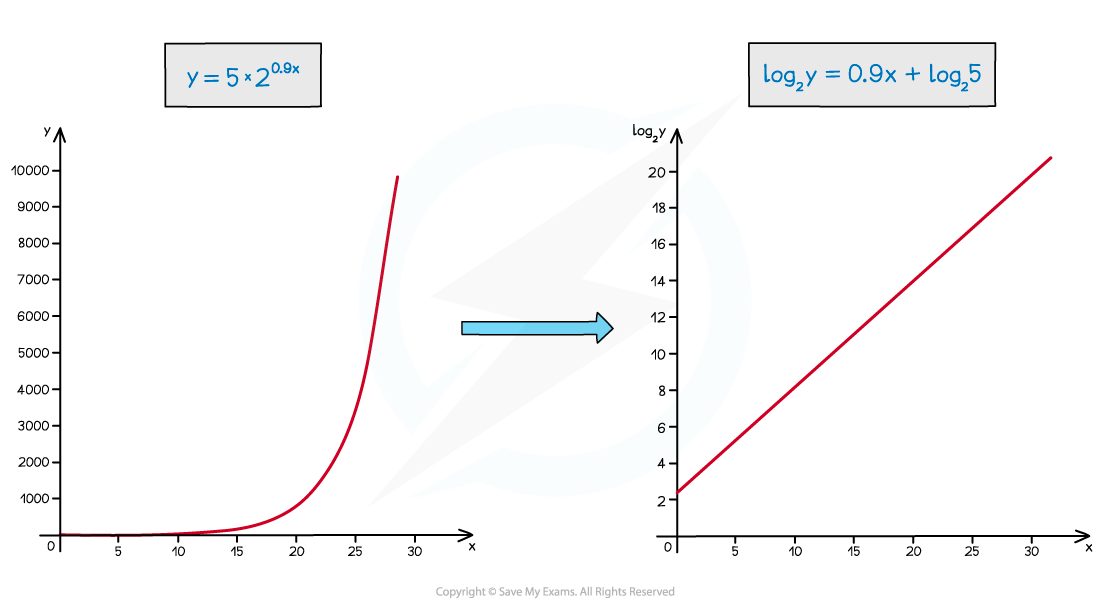
How do I use a logarithmic graph with exponential modelling?
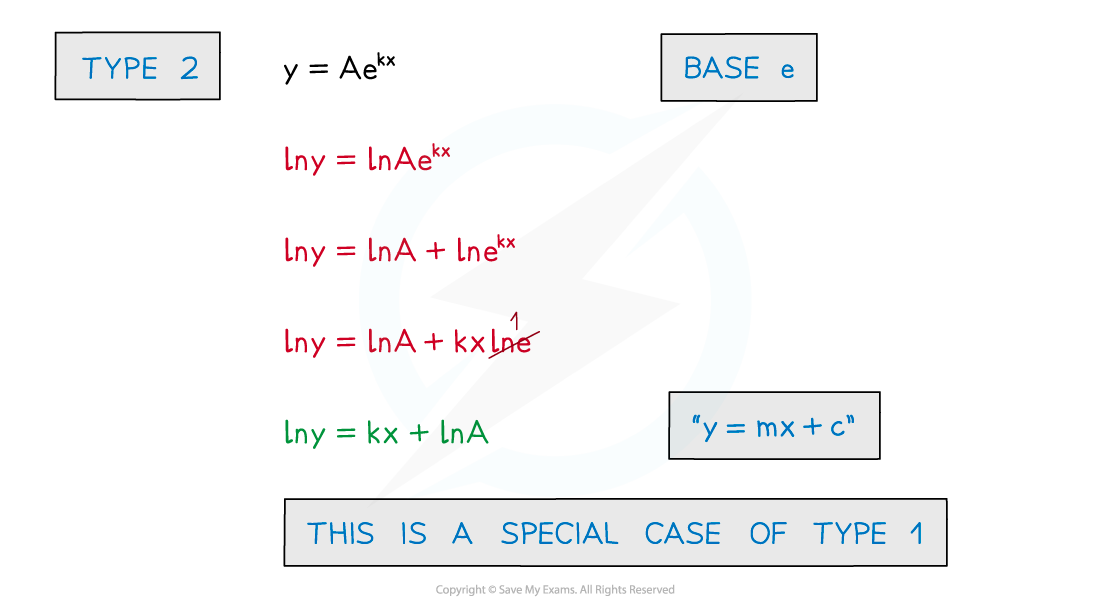
- Exponential models are of the form
- y=Abkx (growth)
- y=Ab-kx (decay)
- To use a model to make predictions the values of A, b and k are needed
- A, b and k will usually be estimated from observed data values
- A may be known exactly, as it is a starting/initial value
- Estimating from a straight line graph is easier than from a curve
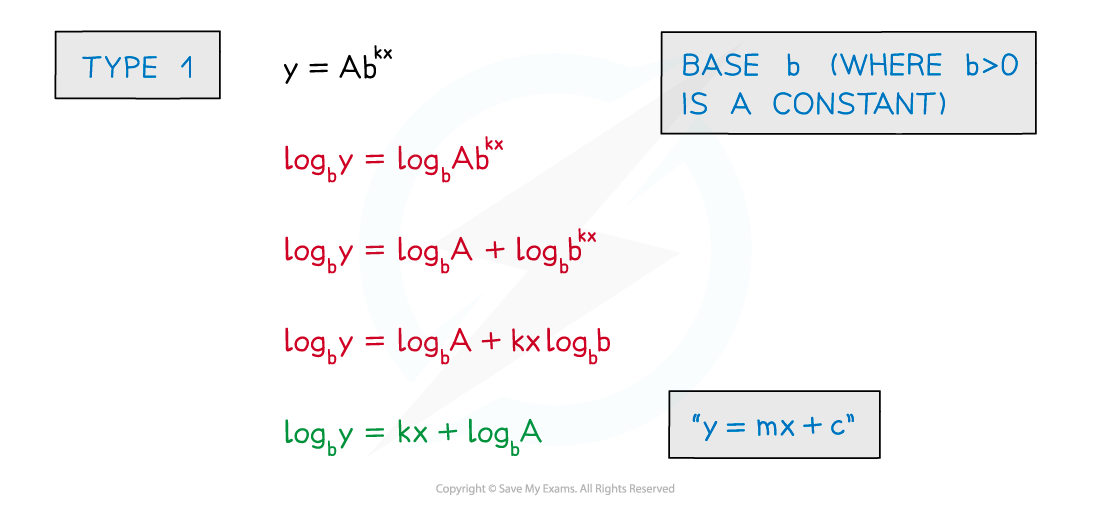
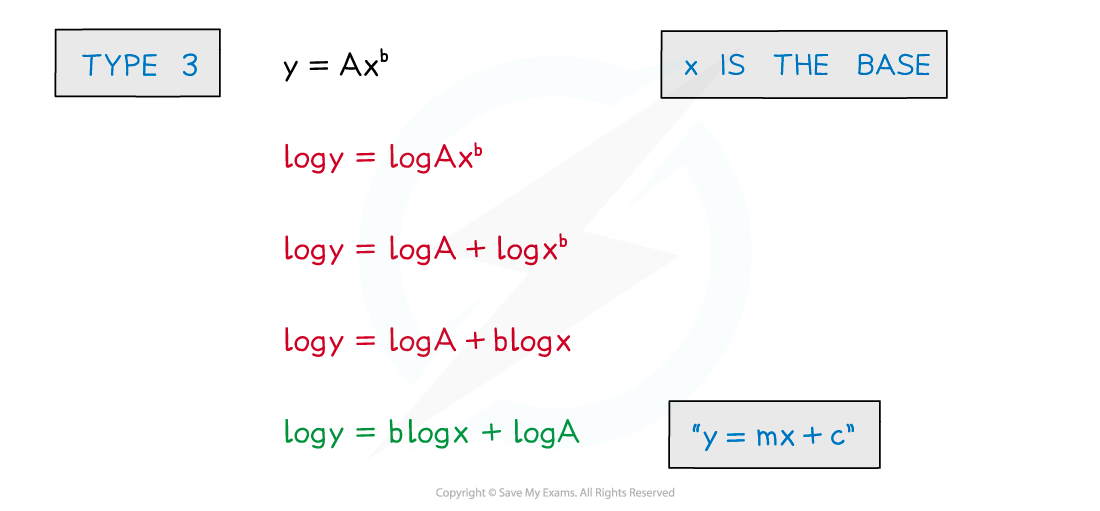

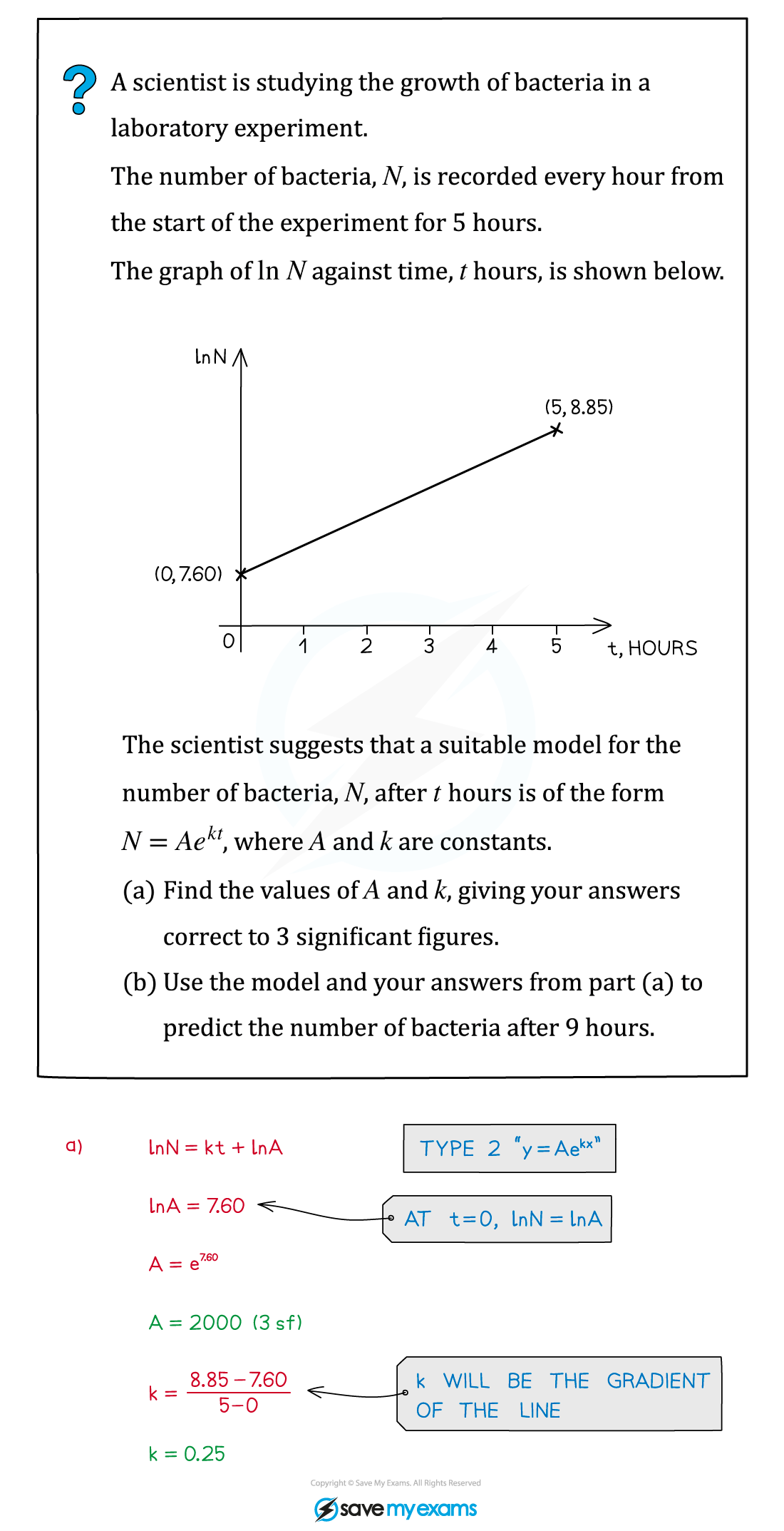
Worked Example

转载自savemyexams

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








