IB DP Physics: SL复习笔记6.1.3 Centripetal Acceleration

• For an object moving in a circle:
  • The acceleration is towards the centre of the circle
  • The magnitude of the centripetal acceleration a is:

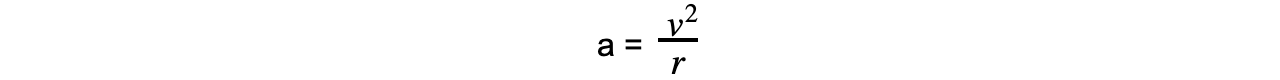
• Where:
  • a = centripetal acceleration (m s^–2)
  • v = linear speed (m s^–1)
  • r = radius of orbit (m)

• Uniform circular motion is continuously changing direction, and therefore is constantly changing velocity
  • The object must therefore be accelerating
• This is called the centripetal acceleration

Direction of the Centripetal Acceleration

• The centripetal acceleration is perpendicular to the direction of the linear velocity
  • Centripetal means it acts towards the centre of the circular path

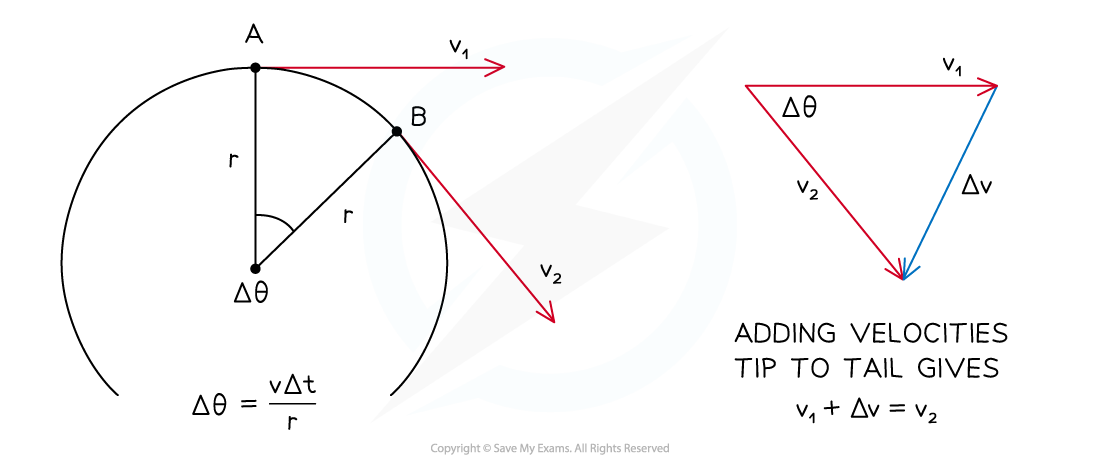
Slide a ruler parallel to Δv towards the circle. Midway between A and B, Δv points towards the centre of the circle. This is the same direction as the centripetal acceleration

• If an object moves through a section of a circle during some time Δt
• The change in velocity during this time is Δv
• The centripetal acceleration is Δv (a vector) divided by Δt (a scalar)
  • The centripetal acceleration points in the same direction as the change in velocity Δv

• The centripetal acceleration is caused by a centripetal force of constant magnitude that also acts perpendicular to the direction of motion (towards the centre)
• There is no component of the centripetal force in the direction of the velocity
  • Therefore, there is no acceleration in the direction of the velocity
  • Hence, there is uniform motion at constant speed
• Therefore, the centripetal acceleration and force act in the same direction

Magnitude of the Centripetal Acceleration

• In the diagram above notice how the angle Δθ is defined in terms of the arc length vΔt and the radius r
• v is the magnitude of v1 and v2

• Notes for deriving the equation for centripetal acceleration:
  • The vector triangle should be formed so that Δv is horizontal
  • The velocity vectors v should be of the same length
  • Hence, the vertical line bisects the angle Δθ and the vector Δv
  • Use trigonometry for one of the small triangles
  • The small-angle approximation requires that the angles are in radians
  • The two equations for Δθ lead to the magnitude of the centripetal acceleration

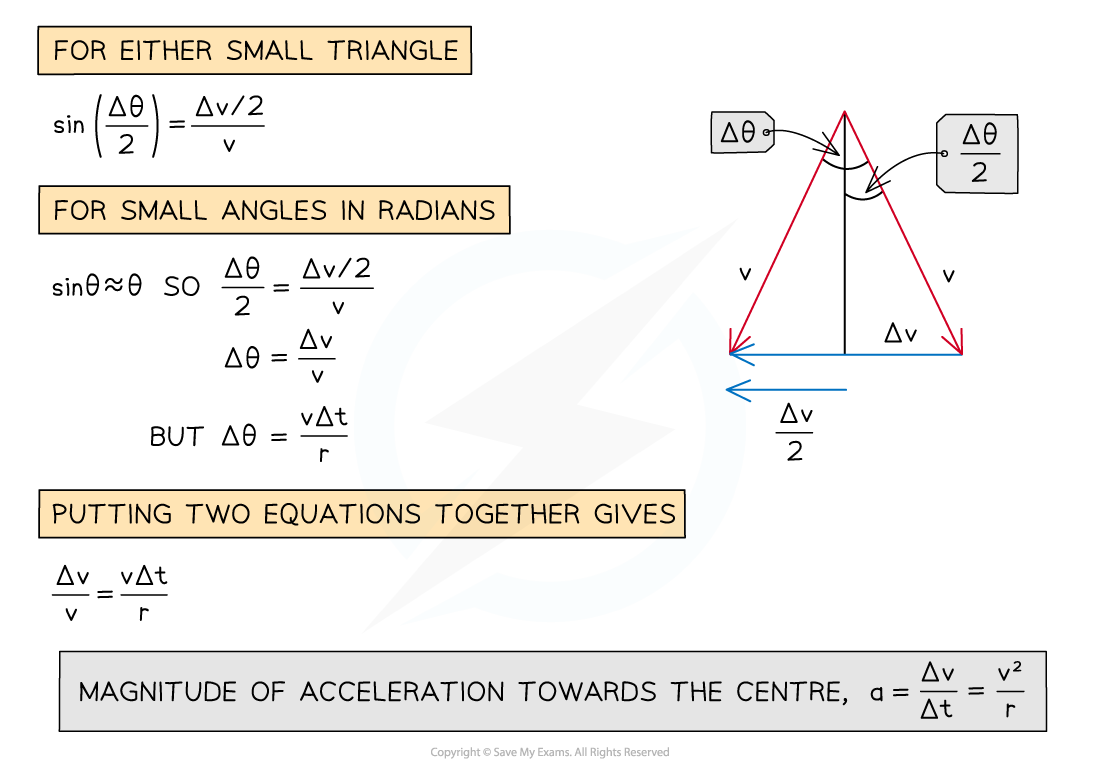
Deriving the equation for the magnitude of the centripetal acceleration

• This leads to the equation for centripetal acceleration:

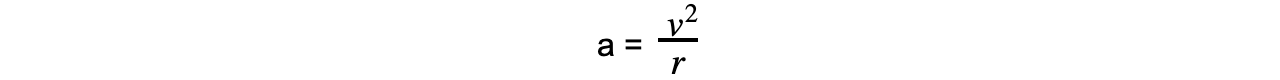
• Using the equation relating angular speed ω and linear speed v:

v = r⍵

• These equations can be combined to give another form of the centripetal acceleration equation:

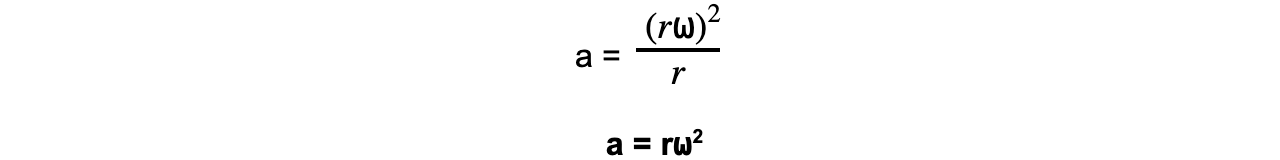
• Where:
  • a = centripetal acceleration (m s⁻²)
  • v = linear speed (m s⁻¹)
  • ⍵ = angular speed (rad s⁻¹)
  • r = radius of the orbit (m)

• Uniform centripetal acceleration is defined as:

The acceleration of an object towards the centre of a circle when an object is in motion (rotating) around a circle at a constant speed

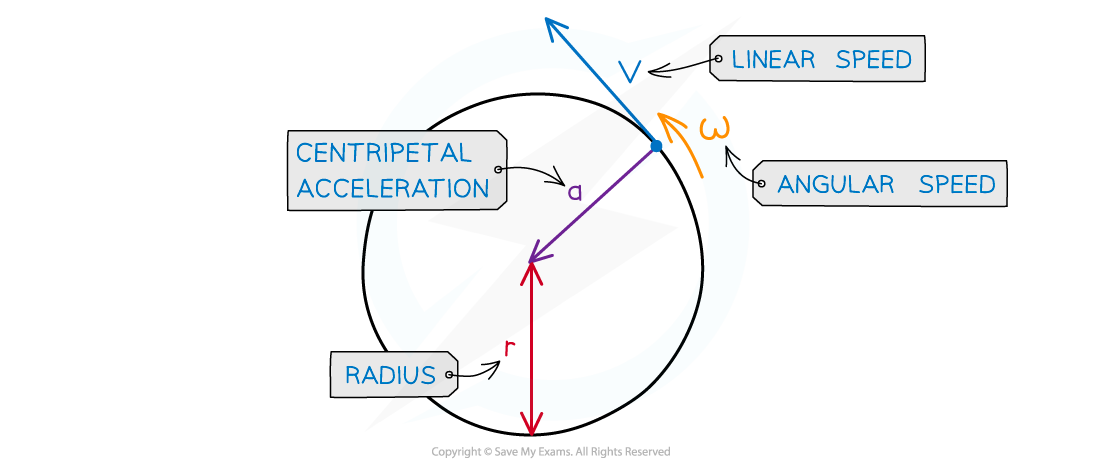
Centripetal acceleration is always directed toward the centre of the circle and is perpendicular to the object’s velocity

Step 1: List the known quantities

• • Radius of the drum, r = ½ × 50 cm = 25 cm

Step 2: Convert the revolutions per minute to revolutions per second

1200 ÷ 60 = 20 rev s⁻¹

Step 3: Convert revolutions per second to angular speed in radians per second

1 rev s^–1 = 2π rad s^–1

20 rev s^–1 = 40π rad s^–1 = ω

Step 4: Write the equation linking centripetal acceleration and angular speed

a = rω²

Step 5: Calculate the centripetal acceleration

a = (25 × 10⁻²) × (40π)²

Step 6: State the final answer

a = 3900 m s−2 (2 s.f.)