- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: SL复习笔记5.4.2 Magnetic Force on a Charge
Magnetic Force on a Charge
Calculating Magnetic Force on a Moving Charge
- The magnetic force on an isolating moving charge, such an electron, is given by the equation:
F = BQv sinθ
- Where:
- F = force on the charge (N)
- B = magnetic flux density (T)
- Q = charge of the particle (C)
- v = speed of the charge (m s-1)
- θ = angle between charge’s velocity and magnetic field (degrees)
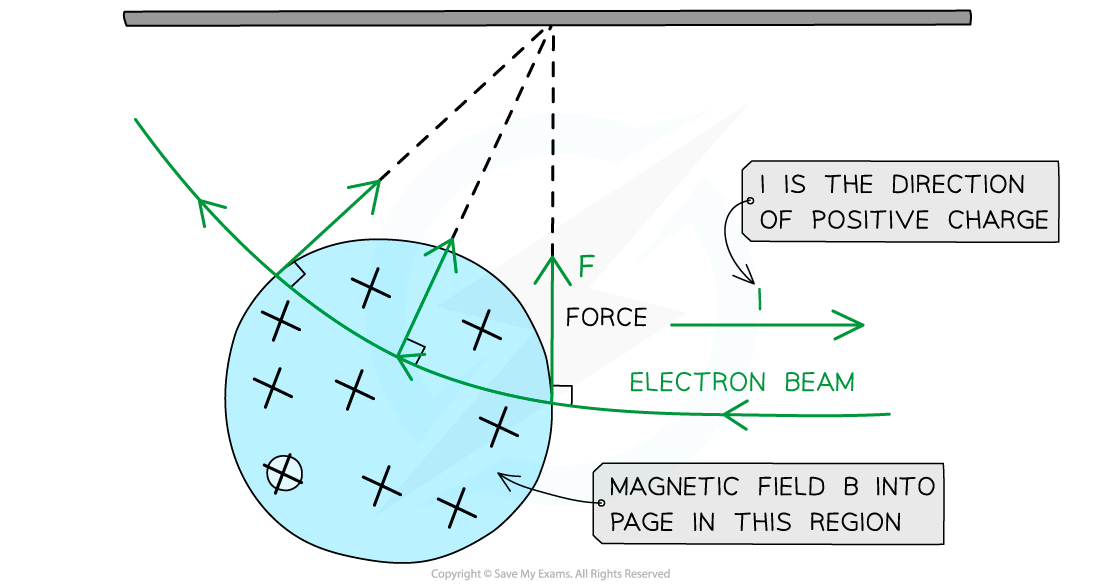
The force on an isolated moving charge is perpendicular to its motion and the magnetic field B
- Equivalent to the force on a wire, if the magnetic field B is perpendicular to the direction of the charge’s velocity, the equation simplifies to:
F = BQv
- According to Fleming’s left hand rule:
- When an electron enters a magnetic field from the left, and if the magnetic field is directed into the page, then the force on it will be directed upwards
- The equation shows:
- If the direction of the electron changes, the magnitude of the force will change too
- The force due to the magnetic field is always perpendicular to the velocity of the electron
- Note: this is equivalent to circular motion
- Fleming’s left-hand rule can be used again to find the direction of the force, magnetic field and velocity
- The key difference is that the second finger representing current I (direction of positive charge) is now the direction of velocity v of the positive charge
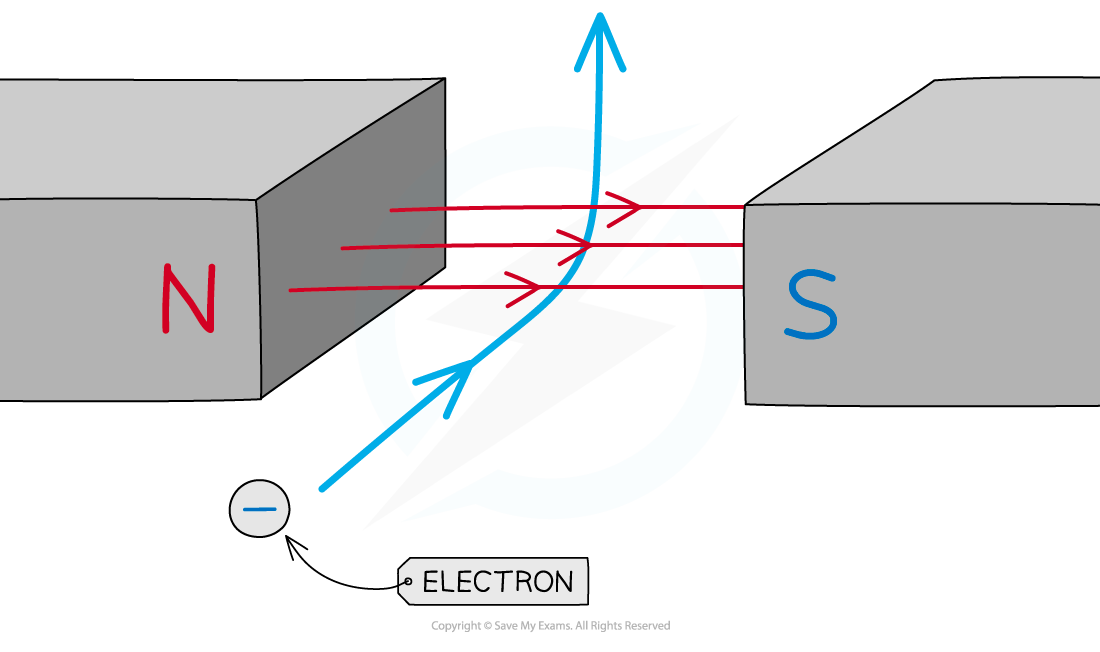
The electron experiences a force upwards when it travels through the magnetic field between the two poles
Worked Example
An electron is moving at 5.3 × 107 m s-1 in a uniform magnetic field of flux density 0.2 T.Calculate the force on the electron when it is moving at 30° to the field, and state the factor it increases by compared to when it travels perpendicular to the field.
Step 1: Write out the known quantities
Speed of the electron, v = 5.3 × 107 m s-1
Charge of an electron, Q = 1.60 × 10-19 C
Magnetic flux density, B = 0.2 T
Angle between electron and magnetic field, θ = 30°
Step 2: Write down the equation for the magnetic force on an isolated particle
F = BQv sinθ
Step 3: Substitute in values, and calculate the force on the electron at 30°
F = (0.2) × (1.60 × 10-19) × (5.3 × 107) × sin(30) = 8.5 × 10-13 N
Step 4: Calculate the electron force when travelling perpendicular to the field
F = BQv = (0.2) × (1.60 × 10-19) × (5.3 × 107) = 1.696 × 10-12 N
Step 5: Calculate the ratio of the perpendicular force to the force at 30°
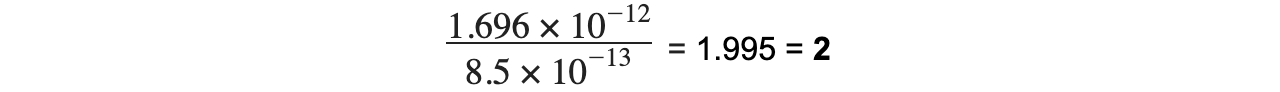
Therefore, the force on the electron is twice as strong when it is moving perpendicular to the field than when it is moving at 30° to the field
Motion of a Charged Particle in a Uniform Magnetic Field
- A charged particle in uniform magnetic field which is perpendicular to its direction of motion travels in a circular path
- This is because the magnetic force FB will always be perpendicular to its velocity v
- FB will always be directed towards the centre of the path
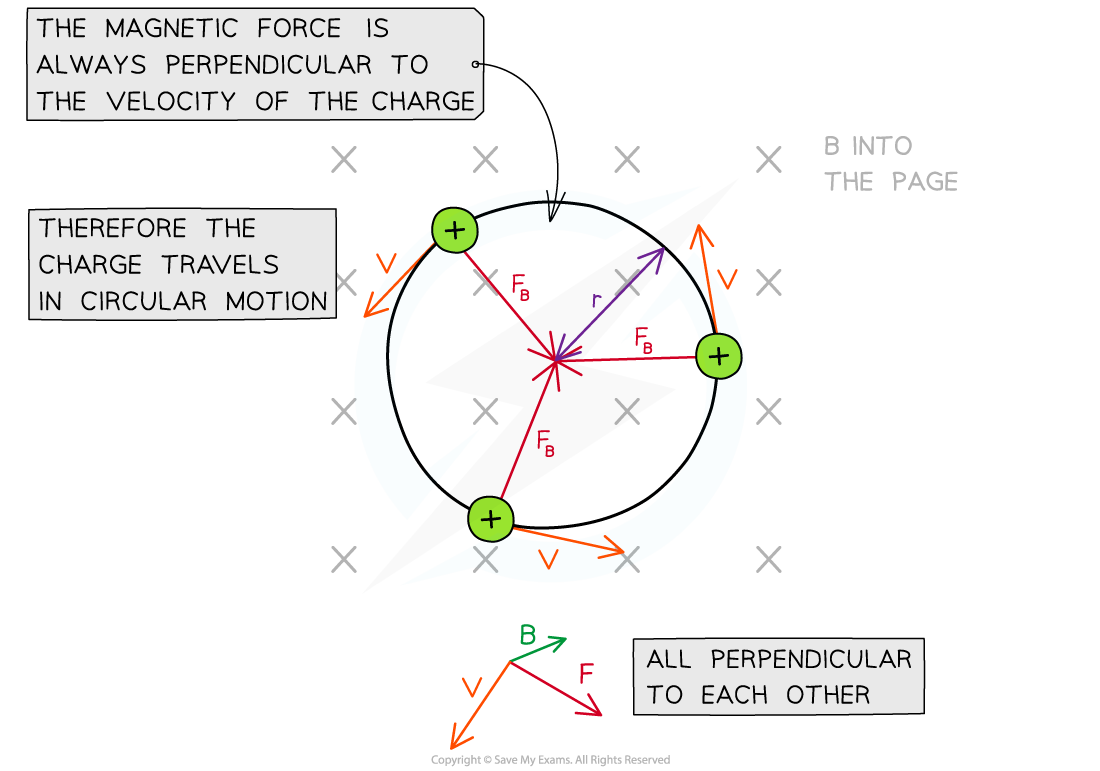
A charged particle moves travels in a circular path in a magnetic field
- The magnetic force FB provides the centripetal force on the particle
- Recall the equation for centripetal force:
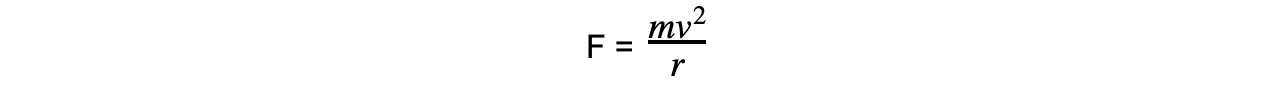
- Where:
- m = mass of the particle (kg)
- v = linear velocity of the particle (m s-1)
- r = radius of the orbit (m)
- Equating this to the force on a moving charged particle gives the equation:
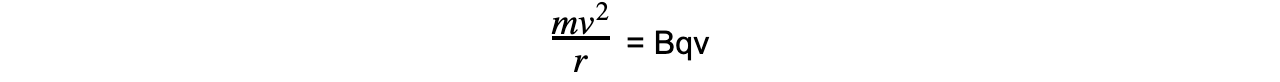
- Rearranging for the radius r obtains the equation for the radius of the orbit of a charged particle in a perpendicular magnetic field:
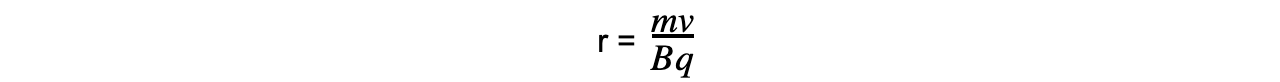
- This equation shows that:
- Faster moving particles with speed v move in larger circles (larger r): r ∝ v
- Particles with greater mass m move in larger circles: r ∝ m
- Particles with greater charge q move in smaller circles: r ∝ 1 / q
- Particles moving in a strong magnetic field B move in smaller circles: r ∝ 1 / B
Worked Example
An electron with charge-to-mass ratio of 1.8 × 1011 C kg-1 is travelling at right angles to a uniform magnetic field of flux density 6.2 mT. The speed of the electron is 3.0 × 106 m s-1.Calculate the radius of the circle path of the electron.
Step 1: Write down the known quantities
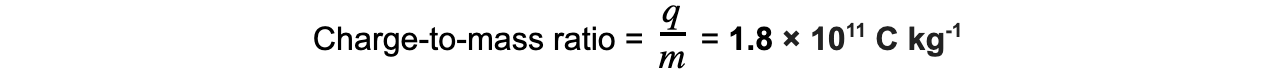
Magnetic flux density, B = 6.2 mT
Electron speed, v = 3.0 × 106 m s-1
Step 2: Write down the equation for the radius of a charged particle in a perpendicular magnetic field
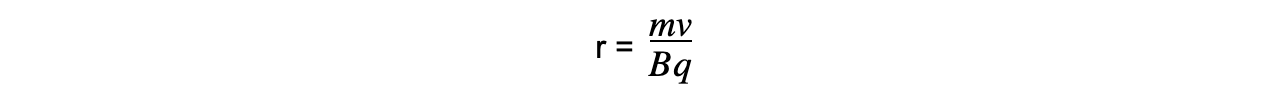
Step 3: Substitute in values
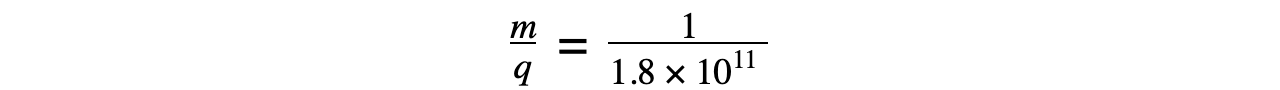
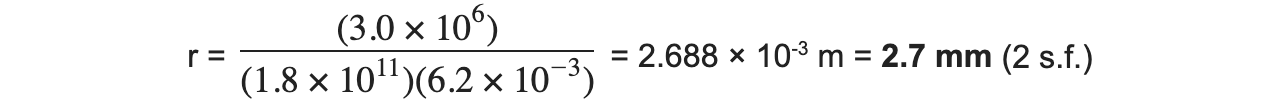
Exam Tip
- Remember not to mix this up with F = BIL!
- F = BIL is for a current carrying conductor
- F = Bqv is for an isolated moving charge (which may be inside a conductor)
- It is important to note that when the moving charge is traveling along the field direction - precisely with or against the field lines - then there is no magnetic force on that charge!
转载自savemyexams

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








