- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: SL复习笔记4.4.3 Refraction
Refraction
- When light crosses the boundary between two media with different optical densities, it refracts
- At the boundary, the light undergoes a change in direction
- The change in direction depends on which media the light rays pass between:
- From air to glass (less dense to more dense): light bends towards the normal
- The angle of refraction < the angle of incidence
- From glass to air (more dense to less dense): light bends away from the normal
- The angle of refraction > the angle of incidence
- When passing along the normal (perpendicular) the light does not bend at all
- This would be described as transmission
- From air to glass (less dense to more dense): light bends towards the normal
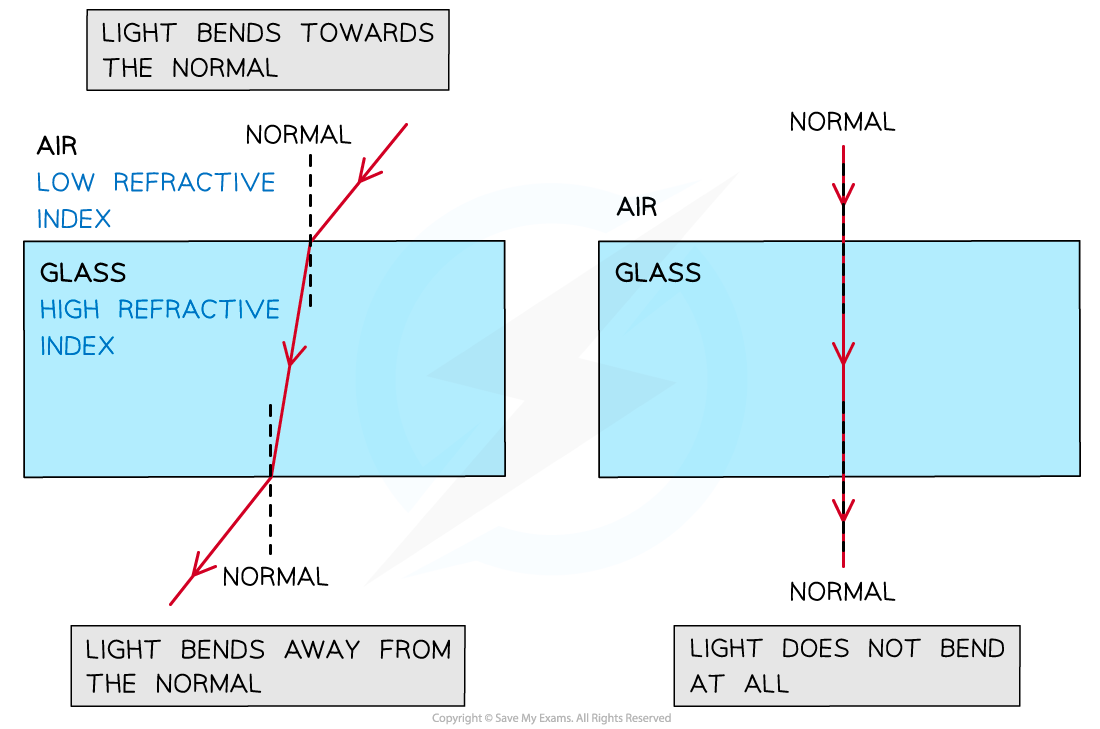
Refraction of light through a glass block
- When light passes from a less dense medium to a more dense medium, such as from air to glass, the refracted light has a lower speed and a shorter wavelength than the incident light
- When light passes from a more dense medium to a less dense medium, such as from glass to air, the refracted light has a higher speed and a longer wavelength than the incident light
- When more than one boundary is shown in a refraction ray diagram, such as light passing through a glass block, the incident ray at the second boundary is the refracted ray from the first boundary
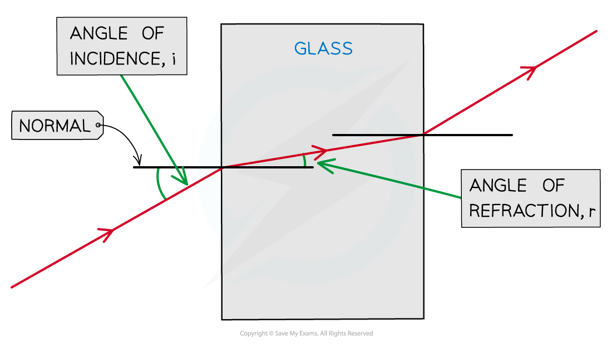
A light ray being refracted at the air-glass boundary
- Together with refraction, reflection might also occur
- When light travels from a less optically dense medium into an optically denser medium, both reflection and refraction always occur
- Light has to be reflected from the object to the eye in order for objects to be visible
- Some of the energy in the incident light is reflected back, while some is transmitted
Absolute Refractive Index
- Transparent media have different optical densities
- Light is transmitted through these media at different speeds
- The absolute refractive index, n, of a transparent medium is a measure of its optical density, and can be calculated as follows:
 Where:
Where:
- n = absolute refractive index of the medium
- c = speed of light in vacuum in metres per second (m s–1)
- v = speed of light in the medium in metres per second (m s–1)
- The value of the speed of light in a vacuum is c = 3.00 × 108 m s–1, as given in the data booklet
- Note that, being a ratio, the absolute refractive index is a dimensionless quantity
- This means that it has no units
- The refractive index of air can be assumed to be n = 1
- Because the speed of light will always be faster than the speed of light in a medium, the refractive index of any other transparent medium is n > 1
Snell's Law
- Snell's Law is:
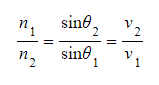 Where:
Where:
- n = absolute refractive index
- θ = angles of incidence and refraction
- v = speed of light in medium
- Snell's Law describes the angle at which light meets the boundary, and the angle at which light leaves the boundary, so that the light travels through the media in the least amount of time
- Light can travel through medium 1 at a speed of v1 due to the optical density n1 of that medium
- Light will approach the boundary at angle θ1
- This is the angle of incidence
- Light can travel through medium 2 at a speed of v2 due to the optical density n2 of that medium
- Light will leave the boundary at angle θ2
- This is the angle of refraction
- To illustrate this, there is a classic thought experiment that uses Fermat's Principle of Light
- Fermat's Principle of Light states that light will travel between two points along the path that will take the least amount of time
- A life guard on a beach sees a swimmer in need of rescue. They can run at 5 m s−1 on the sand and they can swim at 2 m s−1 in the water. What is the fastest path to take?
- The life guard could run on the sand straight to the water and then swim to the person
- The life guard could run on the sand until they are parallel to the person, and then swim directly out to them
- The life guard could run and then swim diagonally in a path that is a straight line from his position in the sand to the position of the swimmer in the water
- Or, the life guard could run diagonally, but so that more of the distance covered is in the sand than in the water
- Some permutation of this answer is where the fastest path will be found
- Using this thought experiment, it can be seen that Snell's Law emerges
- Snell's Law can also be given as:
n1 sin θ1 = n2 sin θ2
- This form of Snell's Law can often be more convenient to use
- When the incident ray is perpendicular to the surface of the boundary, its speed changes, but its direction does not
- Using Snell's Law to explain this
- The angle of incidence is zero, θ1 = 0, therefore, n1 sin0 = n2 sin θ2
- Sin0 = 0
- Anything multiplied by zero is zero, therefore, 0 = n2 sin θ2
- Hence, the refracted angle θ2 must also be zero
- So, there is transmission without refraction
- Using Snell's Law to explain this
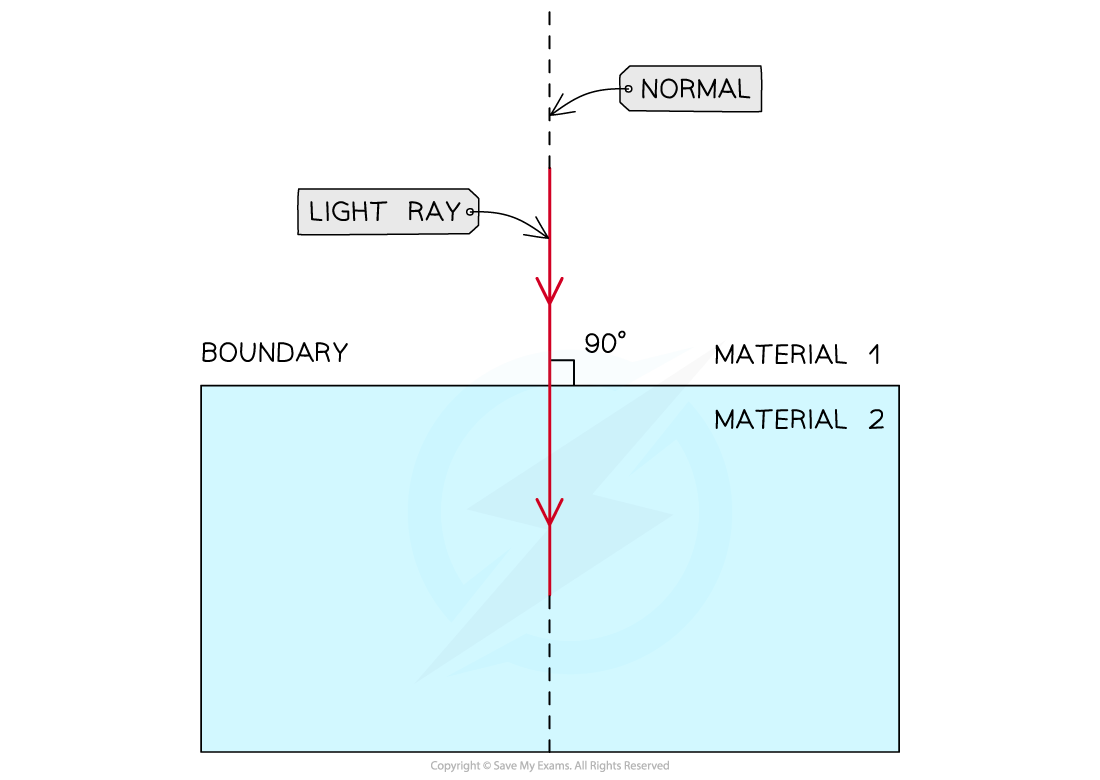
Light travelling along the normal to the boundary between material 1 and material 2
Critical Angle and Total Internal Reflection
- According to Snell's law, when light travels from an optically denser medium into a less optically dense medium, its speed increases and it bends away from the normal
- The angle of refraction is greater than the angle of incidence
- A small amount of light is also reflected back into the optically denser medium
- As the angle of incidence increases, the angle of refraction eventually reaches 90°
- This is known as the critical angle θc:
The angle of incidence which results in an angle of refraction of 90°, after which point, total internal reflection occurs
- The critical angle is important because this is the point at which no light enters the new medium
- For light travelling from an optically denser material 1 into a less optically dense material 2
- If the angle of incidence is smaller than the critical angle (θ1 < θc), the refracted ray bends away from the normal, and the angle of refraction is greater than the angle of incidence (θ2 > θ1)
- If the angle of incidence is equal to the critical angle (θ1 = θc), the refracted ray lies along the boundary between the two materials, and the angle of refraction is equal to 90° (θ2 = 90°)
- If the angle of incidence is greater than the critical angle (θ1 > θc), there is no refracted ray, and all light is reflected back into material 1 (θ2 = θ1)
- This is known as total internal reflection
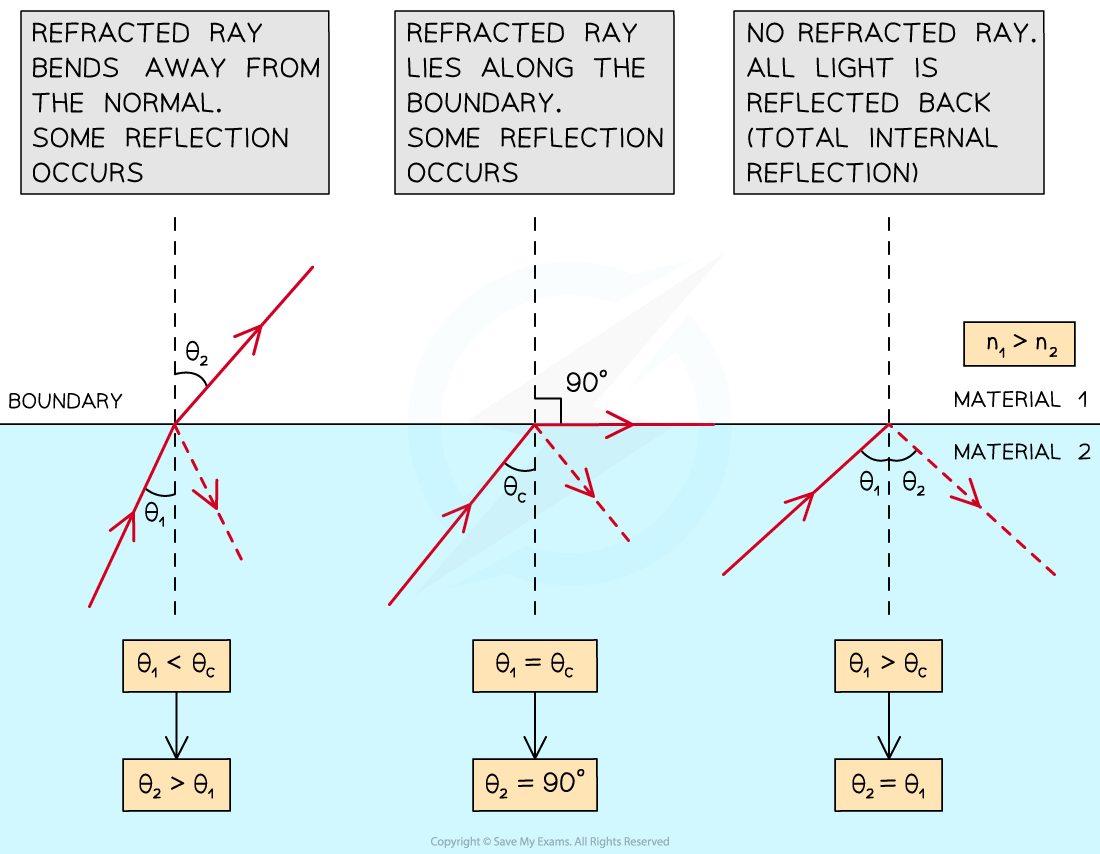
Light travelling from the optically denser material 1 into the less optically dense material 2 at different angles of incidence
- The critical angle of material 1 can be calculated as follows:
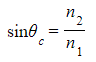
- Where:
- θc = critical angle of material 1 (°)
- n1 = absolute refractive index of material 1
- n2 = absolute refractive index of material 2
Worked Example
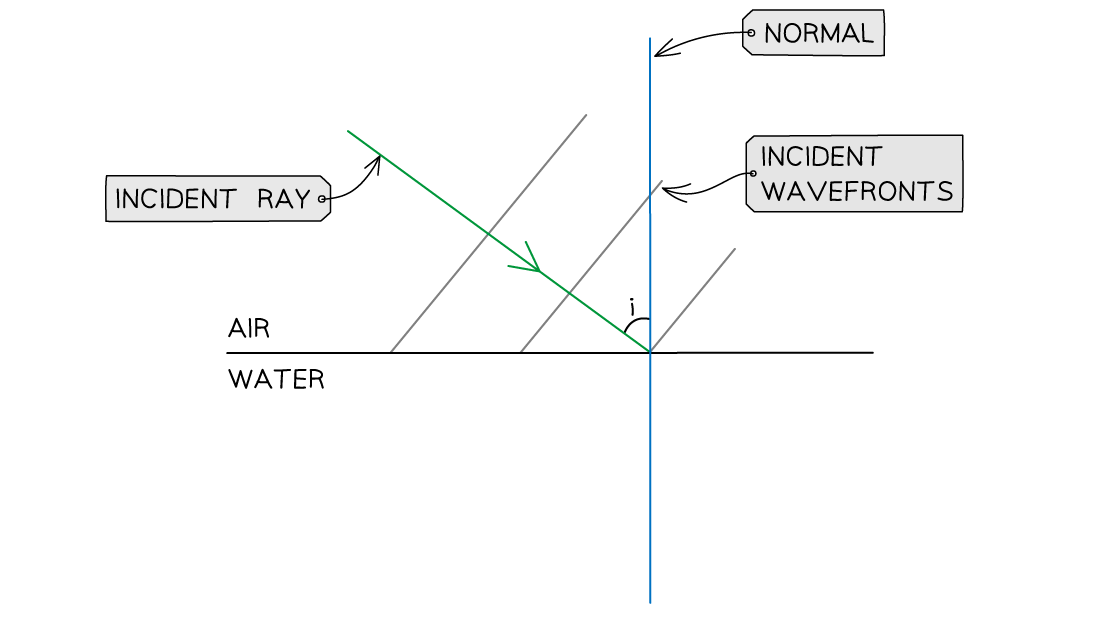
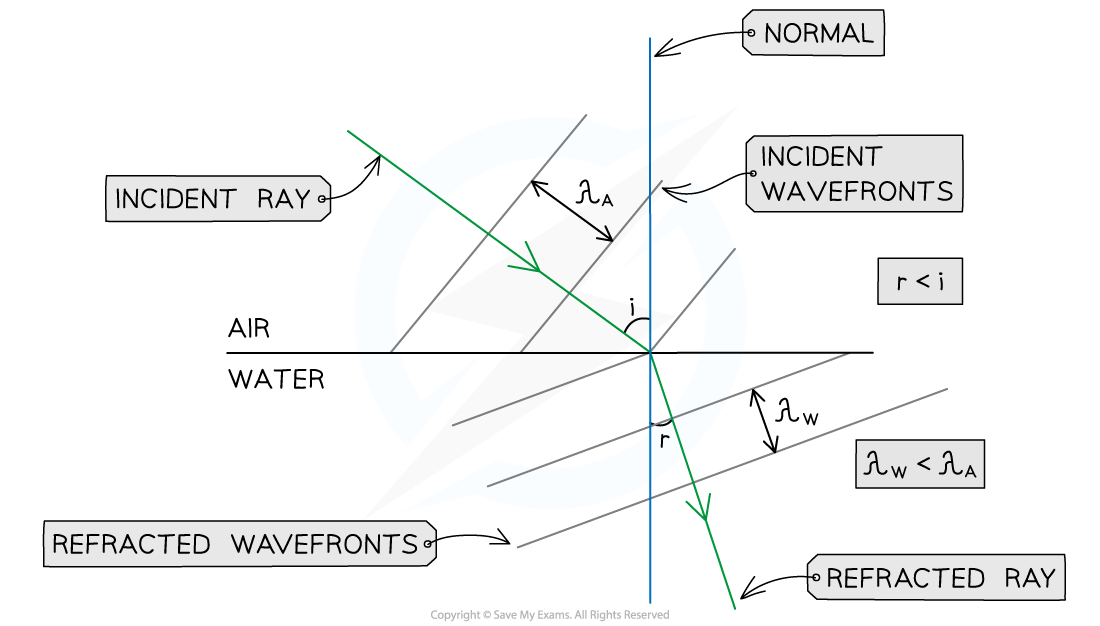
Wavefronts travel from air to water as shown. Add the refracted wavefronts to the diagram.

Step 1: Add the incident ray to mark the direction of the incident waves
-
- The incident ray must be perpendicular to all wavefronts
- Remember to add an arrow pointing towards the air-water boundary

Step 2: Add the normal at the point of incidence
-
- Mark the angle of incidence (i) between the normal and the incident ray
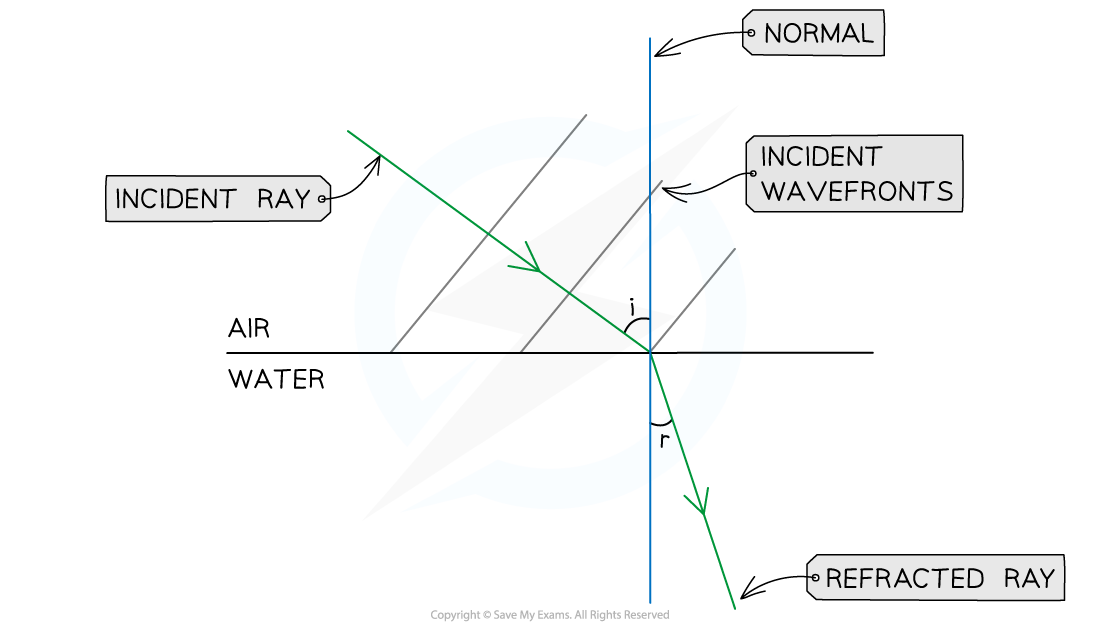
Step 3: Draw the refracted ray into the water
-
- Water is optically denser than air
- The refracted ray must bend towards the normal
- Mark the angle of refraction (r) between the normal and the refracted ray
- r < i, by eye
Step 4: Add three equally spaced wavefronts, all perpendicular to the refracted ray
-
- The refracted wavefronts must be closer to each other than the incident wavefronts, since:
-
-
- The speed v of the waves decreases in water
- The frequency f of the waves stays the same
- The wavelength λ of the waves in water is shorter than the wavelength of the waves in air λW < λA, since v = fλ
-
Worked Example
Light travels from a material with refractive index 1.2 into air. Determine the critical angle of the material.
Step 1: Write down the known quantities
-
- n1 = 1.2
- n2 = 1.0
Step 2: Write down the equation for the critical angle θc
![]()
Step 3: Substitute the numbers into the above equation
![]()
sinθc = 0.83
Step 4: Calculate θc by taking sin–1 of the above equation
θc = sin–1 0.83
θc = 56°
Worked Example
Light travels from air into glass. Determine the speed of light in glass.
- Refractive index of air, n1 = 1.00
- Refractive index of glass, n2 = 1.50
Step 1: Write down the known quantities
-
- n1 = 1.00
- n2 = 1.50
- From the data booklet, c = 3 × 108 m s–1 (speed of light in air)
Step 2: Write down the relationship between the refractive indices of air and glass and the speeds of light in air (v1) and glass (v2)
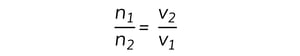
Step 3: Rearrange the above equation to calculate v2
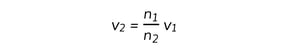
Step 4: Substitute the numbers into the above equation
![]()
v2 = 2 × 108 m s–1
Exam Tip
Always double-check if your calculations for the refractive index are greater than 1. Otherwise, something has definitely gone wrong in your calculation! The refractive index of air might not be given in the question. Always assume that nair= 1
转载自savemyexams

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









