IB DP Physics: SL复习笔记4.2.2 Transverse & Longitudinal Waves

• In mechanical waves, particles oscillate about fixed points
• There are two types of wave: transverse and longitudinal
• The type of wave can be determined by the direction of the oscillations in relation to the direction the wave is travelling

Transverse Waves

• Transverse waves are defined as follows:

A wave in which the particles oscillate perpendicular to the direction of motion and energy transfer

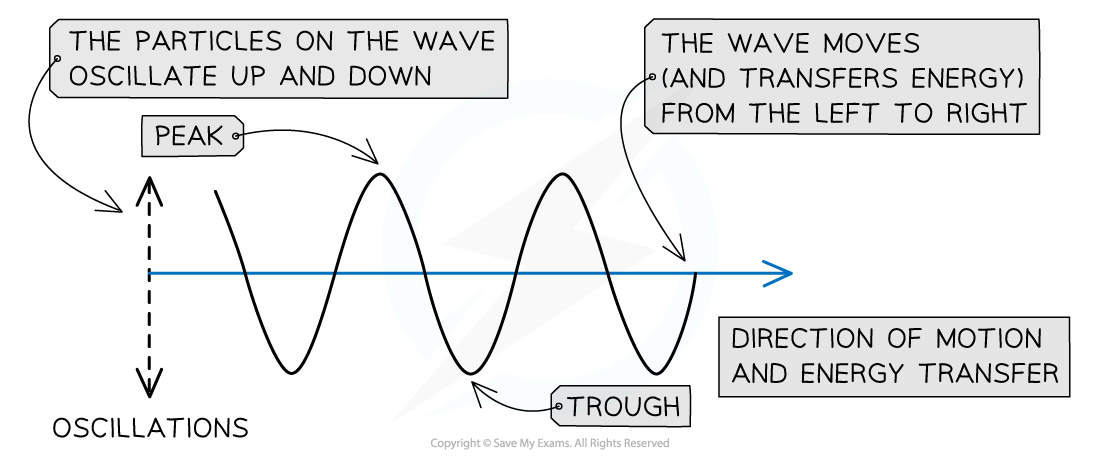
A transverse wave travelling from left to right

• Transverse waves show areas of peaks and troughs
• Examples of transverse waves include:
  • Electromagnetic waves e.g. radio, visible light, UV
  • Vibrations on a guitar string
• Transverse waves do not need particles to propagate, and so they can travel through a vacuum

Longitudinal Waves

• Longitudinal waves are defined as follows:

A wave in which the particles oscillate parallel to the direction of motion and energy transfer

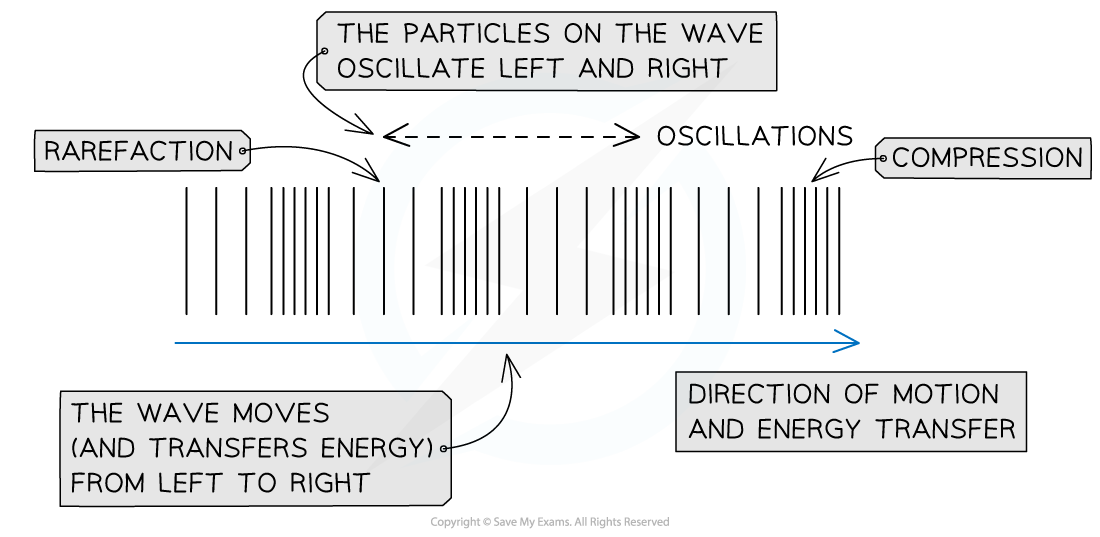
A longitudinal wave travelling from left to right

• As a longitudinal wave propagates, areas of low and high pressure can be observed:
  • A rarefaction is an area of low pressure, with the particles being further apart from each other
  • A compression is an area of high pressure, with the particles being closer to each other
• Sound waves are an example of longitudinal waves
• Longitudinal waves need particles to propagate, and so they cannot travel through a vacuum

• • In transverse waves, the particles oscillate perpendicular to the direction of motion
  • This transverse wave travels from right to left
  • Oscillations will either be up or down
  • Hence point P will either move up or down

Step 2: Determine the next direction of point P

• • Since the wave is moving from right to left, a crest (i.e. a point of maximum displacement above the equilibrium position) will be approaching point P immediately after the time shown
  • Point P will be moving upwards

• Two different types of graphs can be used to represent a travelling wave:
  • Displacement-distance graphs, with displacement x (m) on the y-axis and distance d (m) on the x-axis
  • Displacement-time graphs, with displacement x (m) on the y-axis and time t (s) on the x-axis

• Both transverse and longitudinal waves can be shown on these graphs

Displacement-Distance Graphs

• A displacement-distance graph is also known as a wave profile
• It represents the displacement of many particles on the wave at a fixed instant in time (e.g. t = 0)
• A displacement-distance graph directly provides:
  • The amplitude A of the wave
  • The wavelength λ of the wave

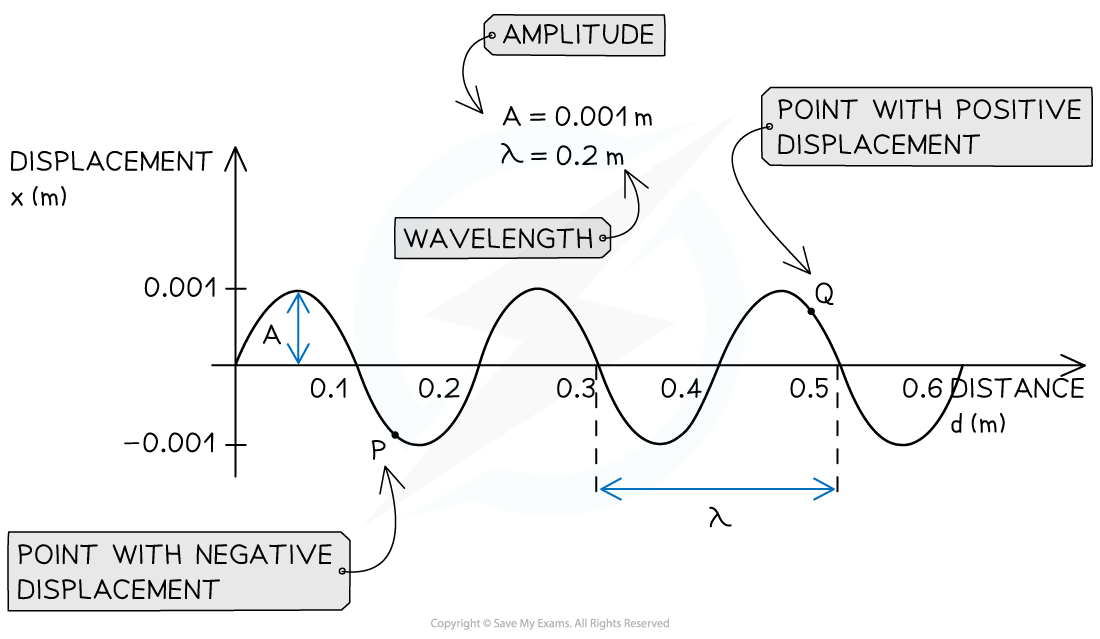
An example of displacement-distance graph for a travelling wave

• In the displacement-distance graph of a transverse wave moving in the horizontal direction:
  • Particles with positive displacement are those moving up
  • Particles with negative displacement are those moving down

• In the displacement-distance graph of a longitudinal wave moving in the horizontal direction:
  • Particles with positive displacement are those moving to the right
  • Particles with negative displacement are those moving to the left
• The wavelength in a longitudinal wave can be figured out from the distance between two rarefactions (or two compressions)

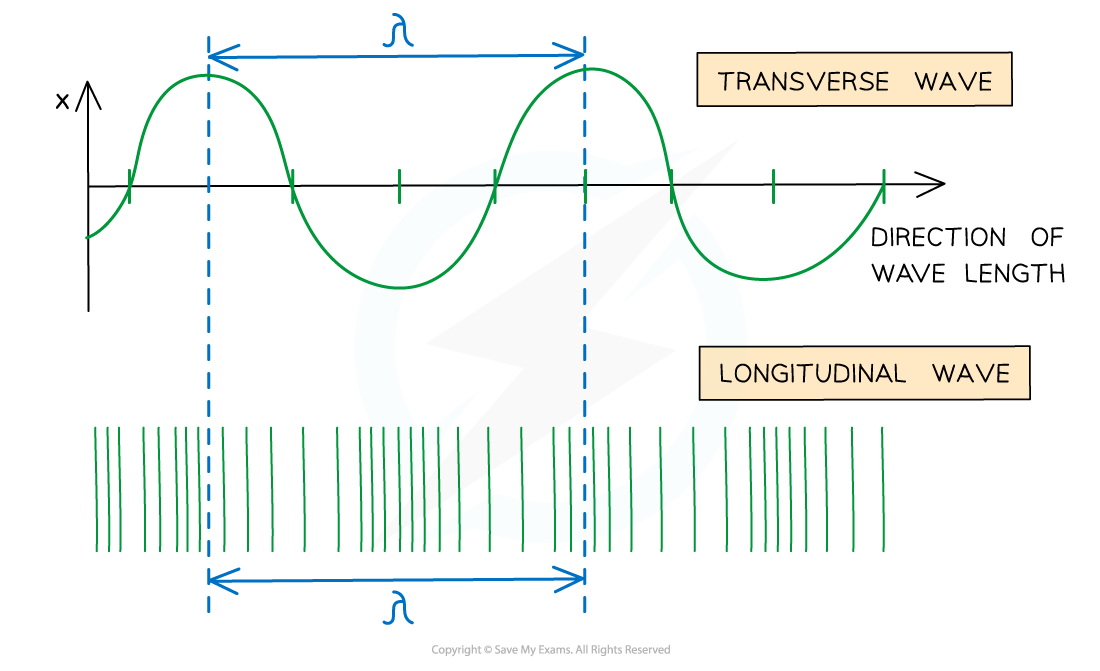
A wavelength on a longitudinal wave is the distance between two compressions or two rarefactions

Displacement-Time Graphs

• A displacement-time graphs represents the variation of the displacement of one particle with time
• A displacement-time graph directly provides:
  • The amplitude A of the wave
  • The period T of the wave

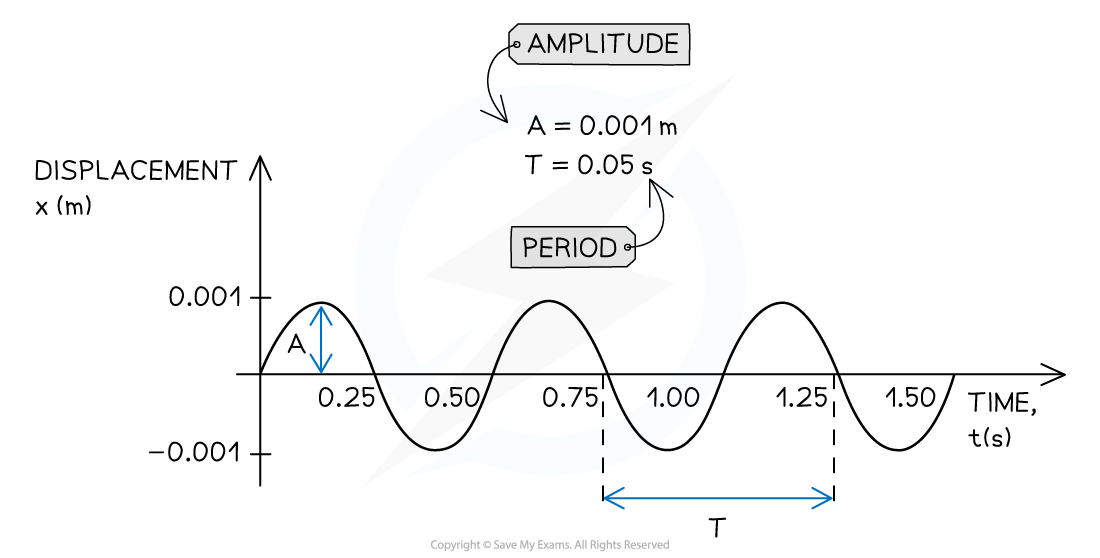
An example of displacement-time graph for a travelling wave

(i) Determine the period T directly from the displacement-time graph

• • Recall that period is defined as the time taken for one complete oscillation
  • Note that you must convert the period from milliseconds (ms) into seconds (s)

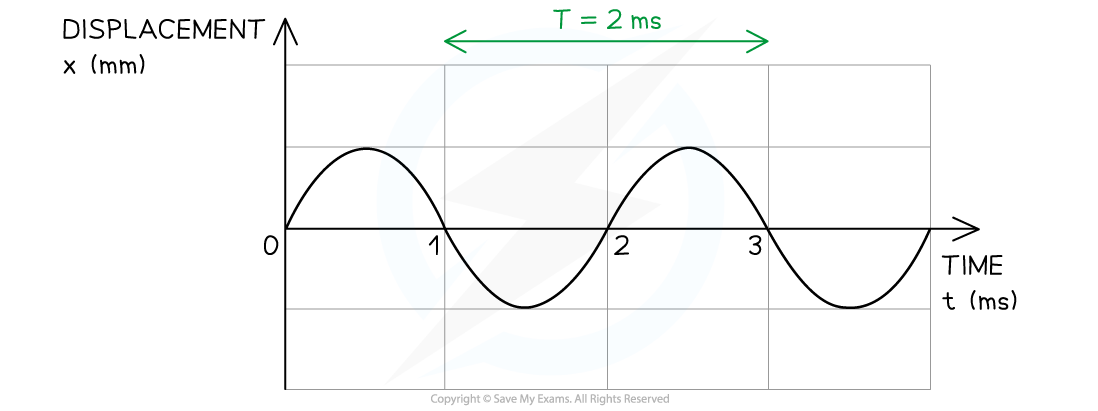
T = 2 × 10^–3 s

(ii) Determine the wavelength of the wave in metres

Step 1: Write down the relationship between frequency f and period T

Step 2: Substitute the value of the period determined in Step 1 into the above equation

f = 500 Hz

Step 3: Write down the wave equation

c = fλ

Step 4: Rearrange the above equation to calculate the wavelength λ

Step 5: Substitute the velocity c = 3 × 10⁸ m s^–1 and the frequency f calculated in Step 2

λ = 6 × 10⁵ m