IB DP Physics: SL复习笔记4.1.2 Simple Harmonic Oscillations

• Simple harmonic motion (SHM) is defined as follows:

The motion of an object whose acceleration is directly proportional but opposite in direction to the object's displacement from a central equilibrium position

• An object is said to perform simple harmonic oscillations when all of the following apply:
  • The oscillations are isochronous
  • There is a central equilibrium point
  • The object's displacement, velocity and acceleration change continuously
  • There is a restoring force always directed towards the equilibrium point
  • The magnitude of the restoring force is proportional to the displacement

• The defining conditions of simple harmonic oscillations are that the restoring force and the acceleration must always be:
  • Directed towards the equilibrium position, and hence, is always in the opposite direction to the displacement
  • Directly proportional to the displacement

a ∝ −x

• Where:
  • a = acceleration (m s⁻²)
  • x = displacement (m)

The Restoring Force

• One of the defining conditions of simple harmonic motion is the existence of a restoring force
• Examples of restoring forces are:
  • The component of the weight of a pendulum's bob that is parallel and opposite to the displacement of the bob
  • The force of a spring, whose magnitude is given by Hooke's law

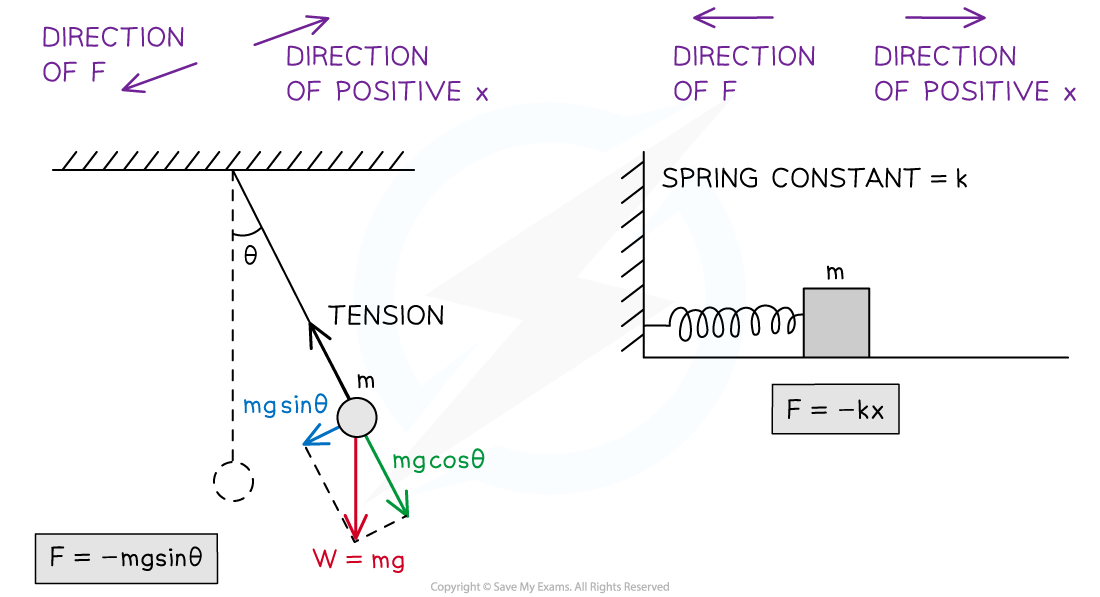
For a pendulum, the restoring force is provided by the component of the bob's weight that is perpendicular to the tension in the pendulum's string. For a mass-spring system, the restoring force is provided by the force of the spring.

• For a mass-spring system in simple harmonic motion, the relationship between the restoring force and the displacement of the object can be written as follows:

F = – kx

• Where:
  • F = restoring force (N)
  • k = spring constant (N m^–1)
  • x = displacement from the equilibrium position (m)

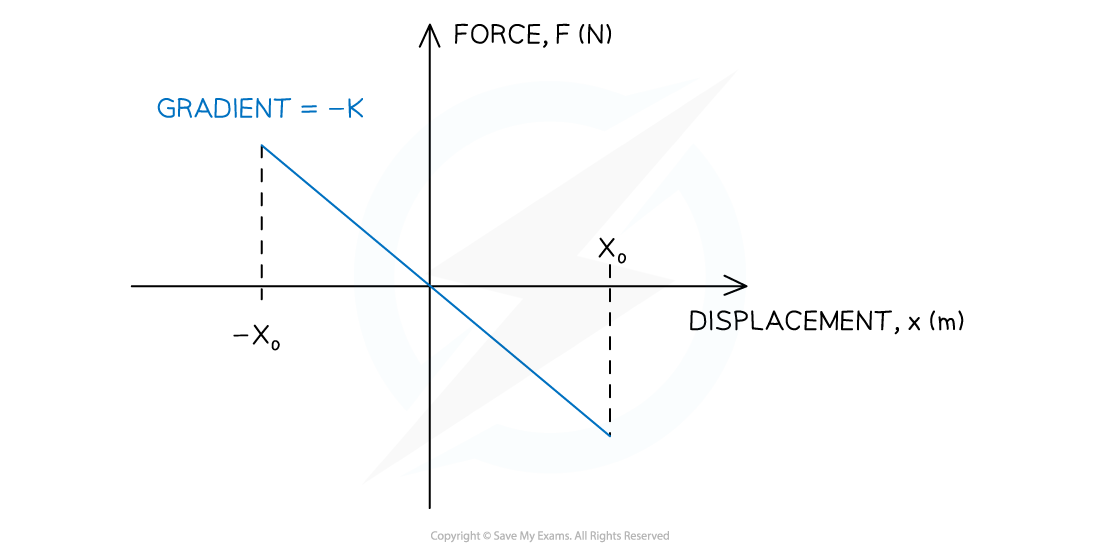
Graph of force against displacement for an object oscillating with SHM

• Force and displacement in SHM have a linear relationship where the gradient of the graph represents the constant
  • In this case, the spring constant k
• An object in SHM will also have a restoring force to return it to its equilibrium position
  • This restoring force will be directly proportional, but in the opposite direction, to the displacement of the object from its equilibrium position

Acceleration & Displacement

• According to Newton's Second Law, the net force on an object is directly proportional to the object's acceleration, F ∝ a for a constant mass

F = ma

• Where
  • F = force (N)
  • m = mass (kg)
  • a = acceleration (m s⁻²)
• Since F = ma (Newton's second law), and F = −kx (Hooke's law), the equations can be set as equal to one another:

ma = – kx

• Rearranging to show the relationship between acceleration and displacement gives:

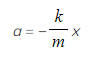• This equation shows that
  • There is a linear relationship between the acceleration of the object moving with simple harmonic motion and its displacement from its equilibrium position

• The minus sign shows that when the mass on the spring is displaced to the right
  • The direction of the acceleration is to the left and vice versa
  • In other words, a and x are always in opposite directions to each other

• This equation shows acceleration is directly proportional but in the opposite direction to displacement for an object in SHM

a ∝ −x

• Therefore, it can be stated that:

a = −kx

• Where
  • a = acceleration
  • k = is a constant but in this instance not the spring constant
  • x = displacement

• Note that in physics, k is the standard letter used for an undefined constant

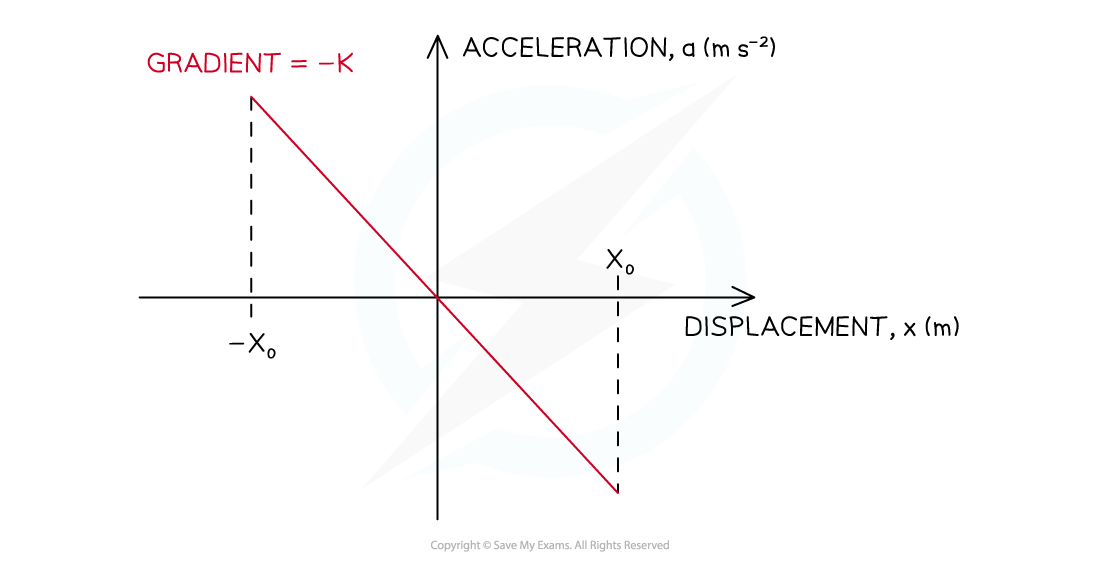
Graph of acceleration against displacement for an object oscillating with SHM

Step 1: List the known quantities

• • Amplitude of the oscillations, x0 = 4.0 cm = 0.04 m
  • Maximum acceleration, a = 2.0 m s^–2
  • Displacement, x = 1.0 cm = 0.01 m

Remember to convert the amplitude of the oscillations and the displacement from centimetres (cm) into metres (m)

Step 2: Recall the relationship between the maximum acceleration a and the displacement x

• • The maximum acceleration a occurs at the position of maximum displacement x = x₀

a = – kx₀

Step 3: Rearrange the above equation to calculate the constant of proportionality k

Step 4: Substitute the numbers into the above equation

k = – 50 s^–2

Step 5: Use this value of k to calculate the acceleration a' when the displacement is x = 0.01 m

a' = – kx

a' = – (– 50) s^–2× 0.01 m

a' = 0.50 m s^–2