IB DP Physics: SL复习笔记1.2.2 Calculating Uncertainties

Precision

• Precise measurements are ones in which there is very little spread about the mean value, in other words, how close the measured values are to each other
• If a measurement is repeated several times, it can be described as precise when the values are very similar to, or the same as, each other
  • Another way to describe this concept is if the random uncertainty of a measurement is small, then that measurement can be said to be precise
• The precision of a measurement is reflected in the values recorded – measurements to a greater number of decimal places are said to be more precise than those to a whole number

Accuracy

• A measurement is considered accurate if it is close to the true value
  • Another way to describe this concept is if the systematic error of a measurement is small, then that measurement can be said to be accurate
• The accuracy can be increased by repeating measurements and finding a mean of the results
• Repeating measurements also helps to identify anomalies that can be omitted from the final results

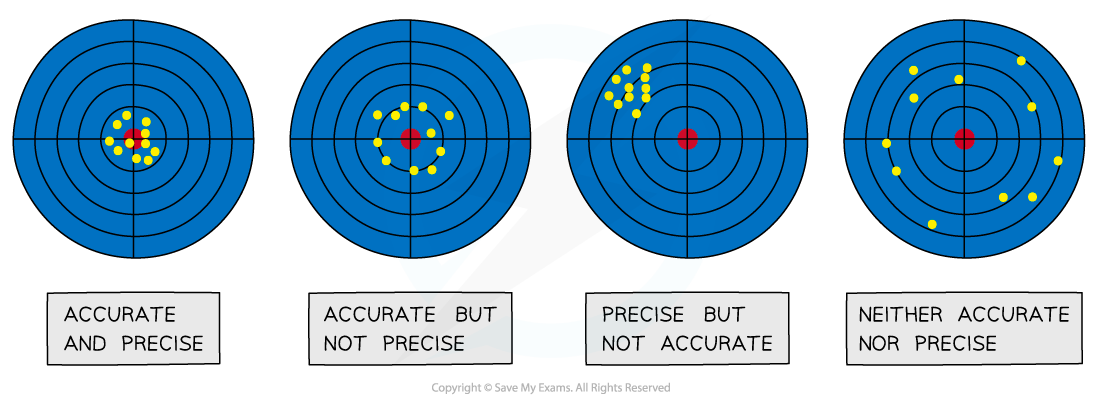
The difference between precise and accurate results

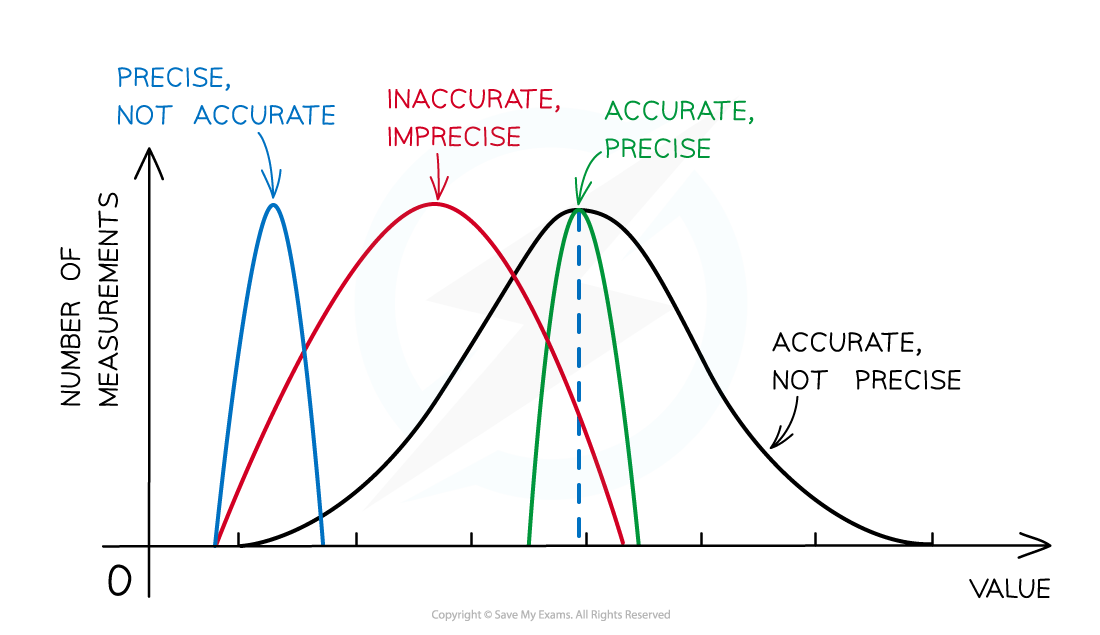
Representing precision and accuracy on a graph

Types of Uncertainty

• There is always a degree of uncertainty when measurements are taken; the uncertainty can be thought of as the difference between the actual reading taken (caused by the equipment or techniques used) and the true value
• Uncertainties are not the same as errors
  • Errors can be thought of as issues with equipment or methodology that cause a reading to be different from the true value
  • The uncertainty is a range of values around a measurement within which the true value is expected to lie, and is an estimate
• For example, if the true value of the mass of a box is 950 g, but a systematic error with a balance gives an actual reading of 952 g, the uncertainty is ±2 g
• These uncertainties can be represented in a number of ways:
  • Absolute Uncertainty: where uncertainty is given as a fixed quantity
  • Fractional Uncertainty: where uncertainty is given as a fraction of the measurement
  • Percentage Uncertainty: where uncertainty is given as a percentage of the measurement

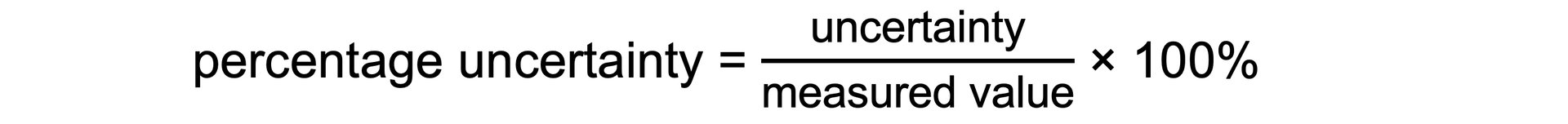
• To find uncertainties in different situations:
  • The uncertainty in a reading: ± half the smallest division
  • The uncertainty in repeated data: half the range i.e. ± ½ (largest - smallest value)
  • The uncertainty in digital readings: ± the last significant digit unless otherwise quoted

How to calculate absolute, fractional and percentage uncertainty

• Always make sure your absolute or percentage uncertainty is to the same number of significant figures as the reading

Combining Uncertainties

• When combining uncertainties, the rules are as follows:

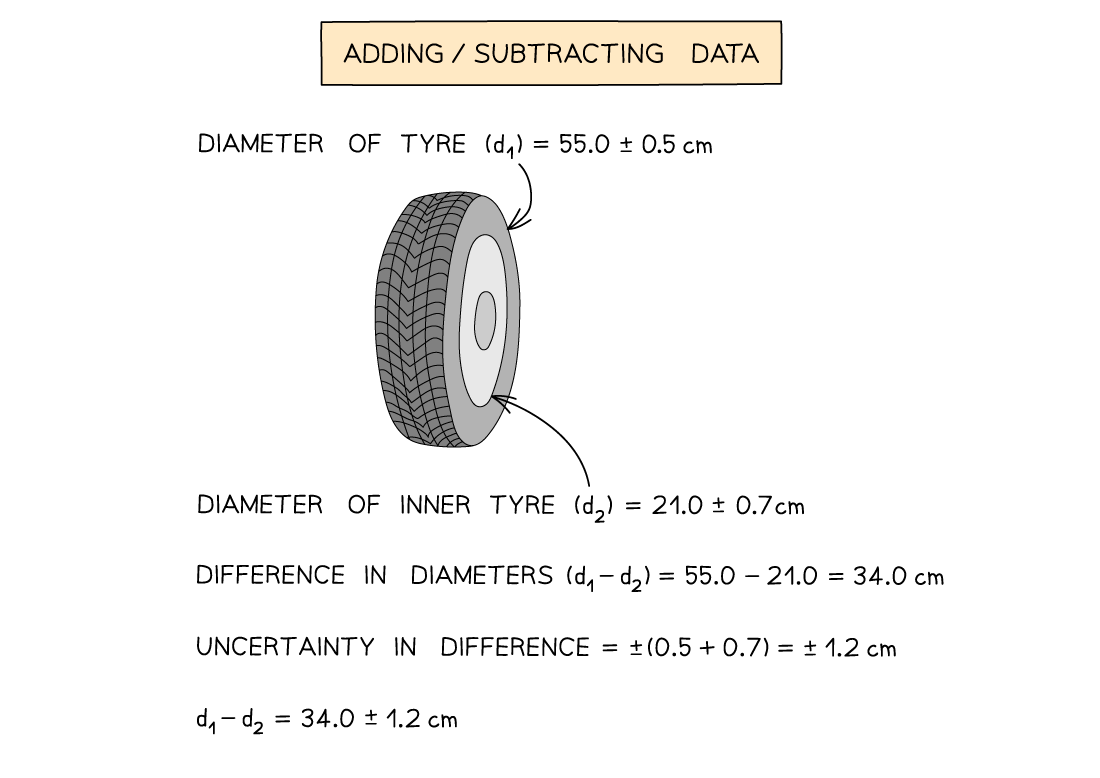
Adding / Subtracting Data

• Add together the absolute uncertainties

Multiplying / Dividing Data

• Add the percentage or fractional uncertainties

Raising to a Power

• Multiply the percentage uncertainty by the power

Step 1: List the known quantities

• • A = 5.0 cm
  • Uncertainty in A, ΔA = 0.1 cm
  • B = 2.5 cm
  • Uncertainty in B, ΔB = 0.1 cm

Step 2: Check the percentage uncertainty of option A

A + B = 5.0 + 2.5 = 7.5 cm

• • The rule for propagating uncertainties for adding data (A + B) is ΔA + ΔB
  • The combined uncertainties are:

0.1 + 0.1 = ± 0.2 cm

• • Therefore, the percentage uncertainty is:

(0.2 ÷ 7.5) × 100 ≈ 2.7%

Step 3: Check the percentage uncertainty of option B

A − B = 5.0 − 2.5 = 2.5 cm

• • The rule for propagating uncertainties for subtracting data (A – B) is ΔA + ΔB
  • The combined uncertainties are:

0.1 + 0.1 = ± 0.2 cm

• • Therefore the percentage uncertainty is:

(0.2 ÷ 2.5) × 100 = 8%

Step 4: Check the percentage uncertainty of option C

A × B = 5.0 × 2.5 = 12.5 cm

• • The rule for propagating uncertainties for multiplying data (A × B) is ΔA/A + ΔB/B
  • The combined uncertainties are:

(0.1 ÷ 5.0) + (0.1 ÷ 2.5) = 0.02 + 0.04 = 0.06

• • Therefore the percentage uncertainty is:

0.06 × 100 = 6%

Step 5: Check the percentage uncertainty of option D

• • A = 5.0 cm and the uncertainty is 0.1 cm
  • Therefore the percentage uncertainty is:

(0.1 ÷ 5.0) × 100 = 2%

Step 6: Compare and select the answer with the smallest percentage uncertainty

• • Comparing the four options, option D is the correct answer as it has a value of 2% which is the smallest percentage uncertainty

Step 1: Find what the value of the quantity will be

√B = √3.0 ≈ 1.73

Step 2: Find the percentage uncertainty of the original

(0.1 ÷ 3.0) × 100 ≈ 3.33%

Step 3: The percentage uncertainty needs to be multiplied by the power of the operation

3.33 × (1 ÷ 2) ≈ 1.67%

Step 4: Apply the percentage uncertainty to the absolute answer

1.67% in decimal form is 0.0167. Therefore: 0.0167 × 1.73 ≈ 0.03

Step 5: State the complete answer

√B = 1.73 ± 0.03