- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Chemistry: SL复习笔记1.2.5 Gas Law Relationships
Gas Law Relationships
- Gases in a container exert a pressure as the gas molecules are constantly colliding with the walls of the container
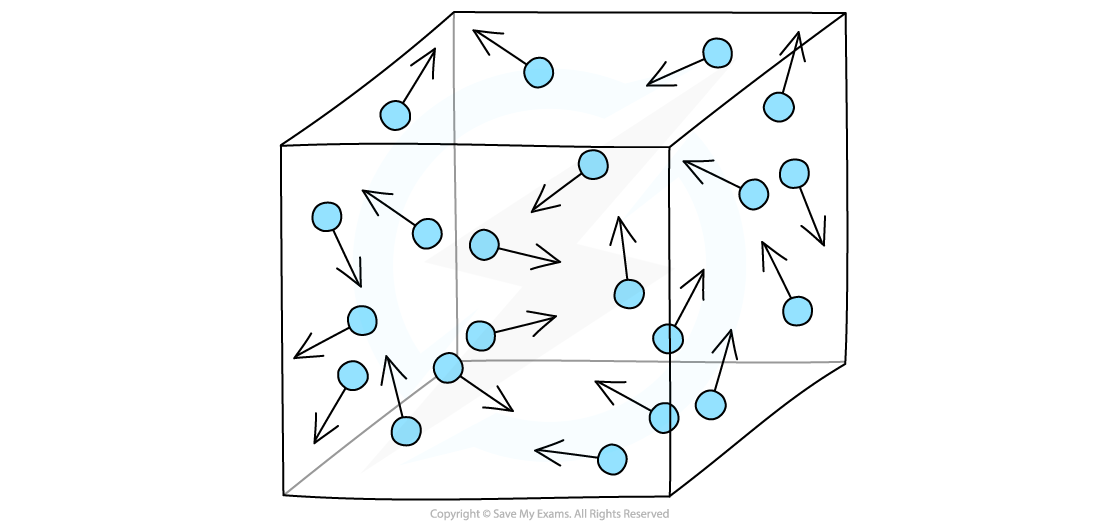
Gas particles exert a pressure by constantly colliding with the walls of the container
Changing gas volume
- Decreasing the volume (at constant temperature) of the container causes the molecules to be squashed together which results in more frequent collisions with the container wall
- The pressure of the gas increases
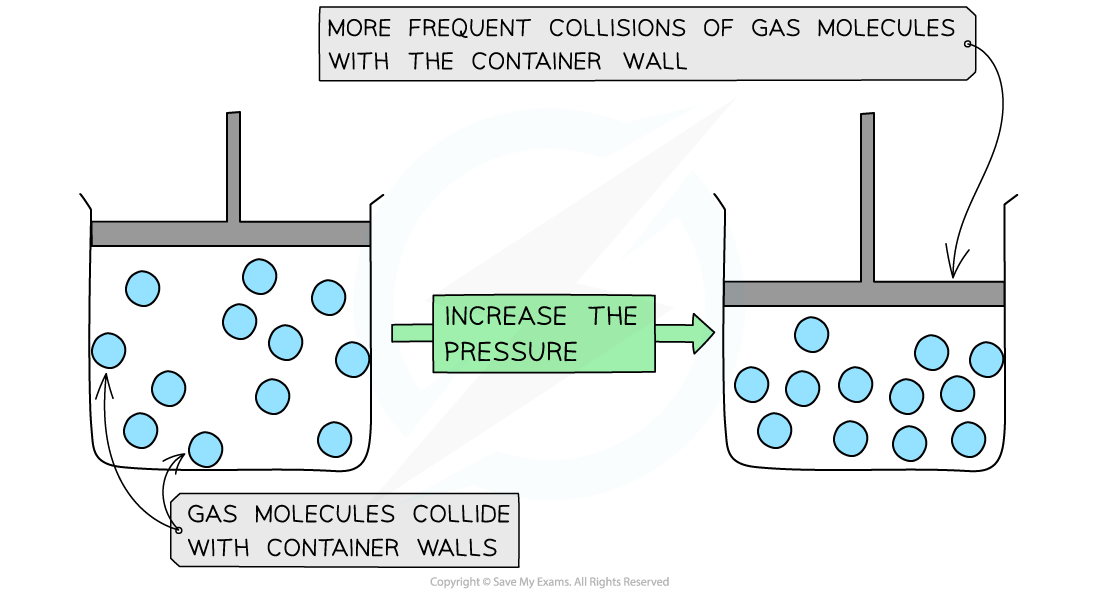
Decreasing the volume of a gas causes an increased collision frequency of the gas particles with the container wall
- The pressure is therefore inversely proportional to the volume (at constant temperature)
- This is known as Boyle's Law
- Mathematically, we say P ∝ 1/V or PV = a constant
- We can show a graphical representation of Boyle's Law in three different ways:
- A graph of pressure of gas plotted against 1/ volume gives a straight line
- A graph of pressure against volume gives a curve
- A graph of PV versus P gives a straight line

Three graphs that show Boyle’s Law
Changing gas temperature
- When a gas is heated (at constant pressure) the particles gain more kinetic energy and undergo more frequent collisions with the container walls
- To keep the pressure constant, the molecules must get further apart and therefore the volume increases
- The volume is therefore directly proportional to the temperature in Kelvin (at constant pressure)
- This is known as Charles' Law
- Mathematically, V ∝ T or V/T = a constant
- A graph of volume against temperature in Kelvin gives a straight line
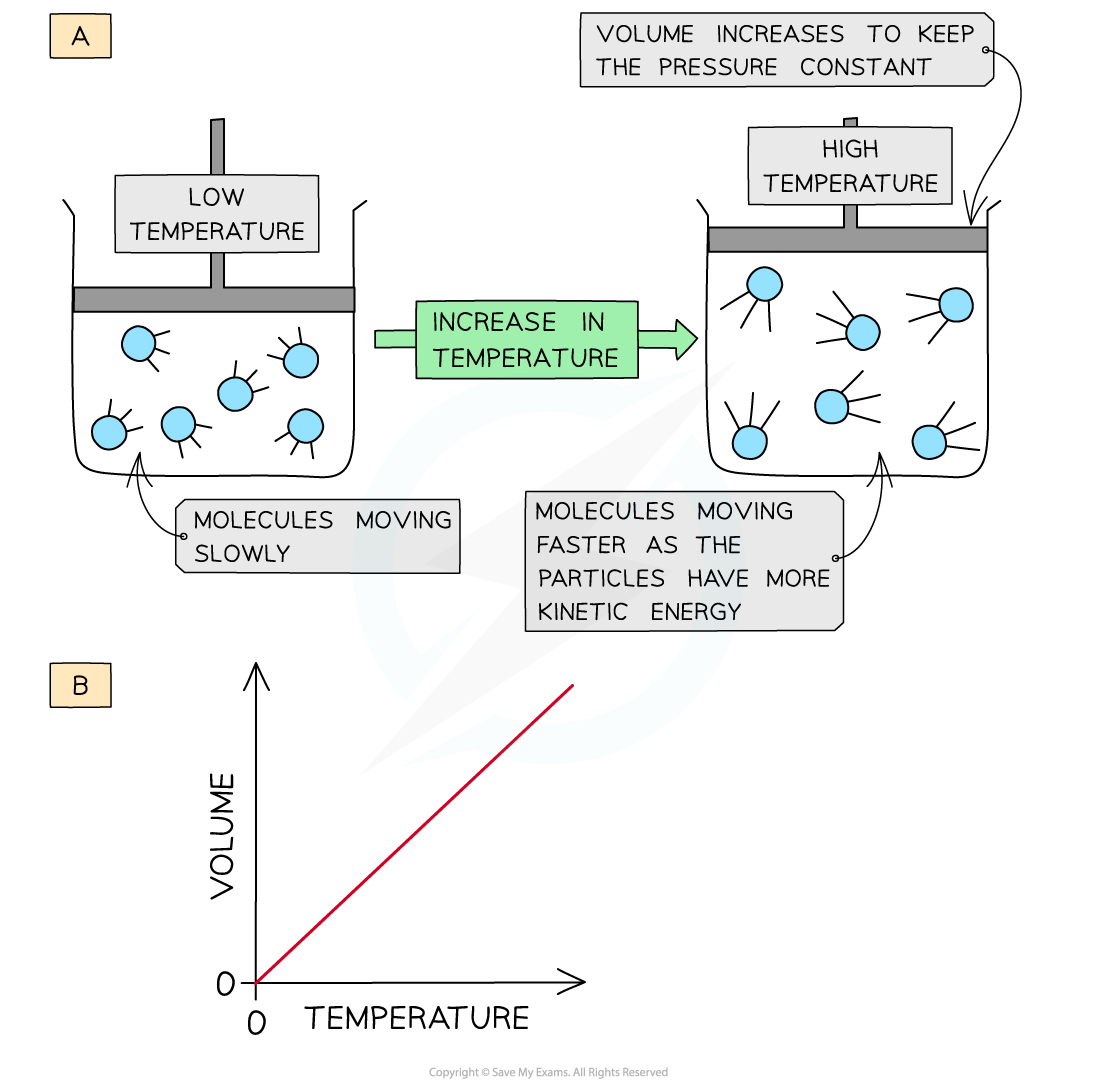
Increasing the temperature of a gas causes an increased collision frequency of the gas particles with the container wall (a); volume is directly proportional to the temperature in Kelvin (b)
Changing gas pressure
- Increasing the temperature (at constant volume) of the gas causes the molecules to gain more kinetic energy
- This means that the particles will move faster and collide with the container walls more frequently
- The pressure of the gas increases
- The temperature is therefore directly proportional to the pressure (at constant volume)
- Mathematically, we say that P ∝ T or P/T = a constant
- A graph of temperature in Kelvin of a gas plotted against pressure gives a straight line
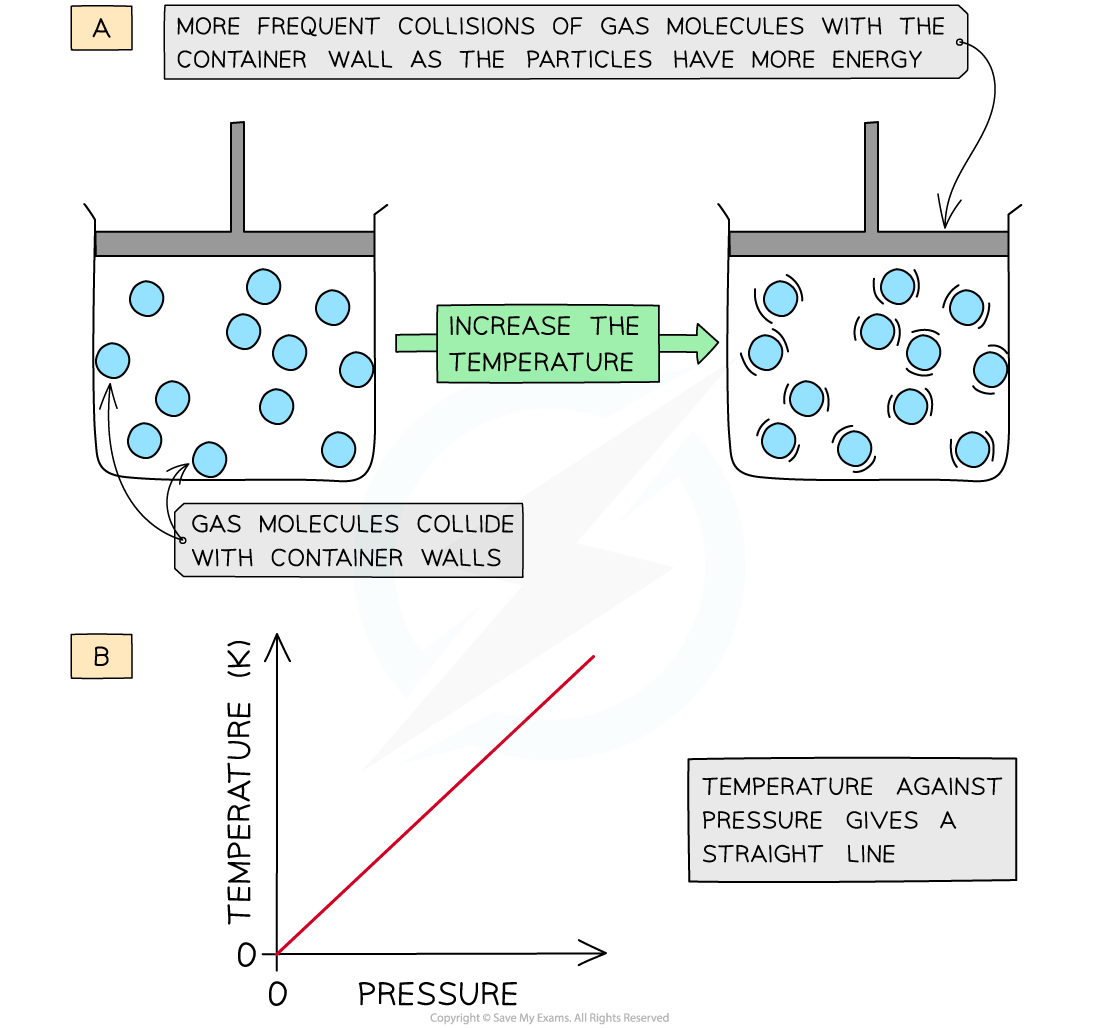
Increasing the temperature of a gas causes an increased collision frequency of the gas particles with the container wall (a); temperature is directly proportional to the pressure (b)
Pressure, volume and temperature
- Combining these three relationships together:
- P/V = a constant
- V/T = a constant
- P/T = a constant
- We can see how the ideal gas equation is constructed
- PV/T = a constant
- PV = a constant x T
- This constant is made from two components, the number of moles, n, and the gas constant, R, resulting in the overall equation:
- PV = nRT
Changing the conditions of a fixed amount of gas
- For a fixed amount of gas, n and R will be constant, so if you change the conditions of a gas we can ignore n and R in the ideal gas equation
- This leads to a very useful expression for problem solving
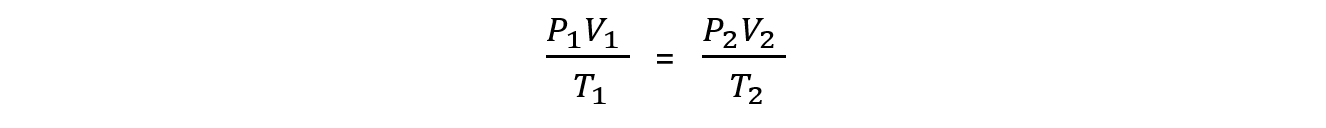
- Where P1, V1 and T1 are the initial conditions of the gas and P2, V2 and T2 are the final conditions
Worked Example
At 25 oC and 100 kPa a gas occupies a volume of 20 dm3. Calculate the new temperature, in oC, of the gas if the volume is decreased to 10 dm3 at constant pressure.
Answer:
Step 1: Rearrange the formula to change the conditions of a fixed amount of gas. Pressure is constant so it is left out of the formula
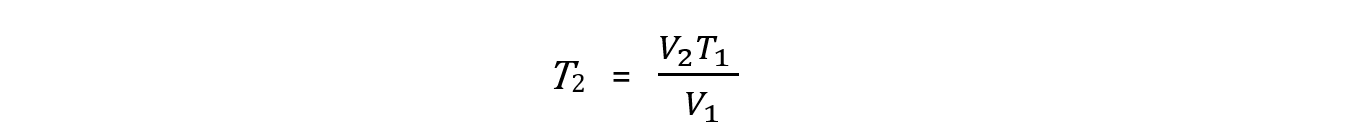 Step 2: Convert the temperature to Kelvin. There is no need to convert the volume to m3 because the formula is using a ratio of the two volumes
Step 2: Convert the temperature to Kelvin. There is no need to convert the volume to m3 because the formula is using a ratio of the two volumes
V1 = 20 dm3
V2 = 10 dm3
T1 = 25 + 273 = 298 K
Step 3: Calculate the new temperature
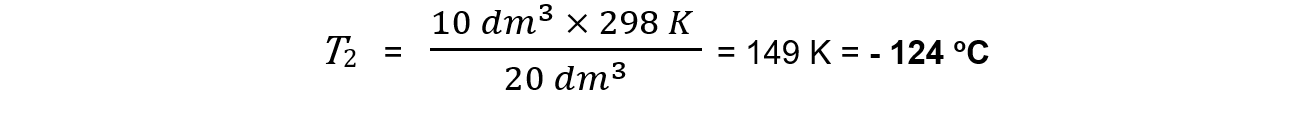
Worked Example
A 2.00 dm3 container of oxygen at a pressure of 80 kPa was heated from 20 oC to 70 oC The volume expanded to 2.25 dm3 . What was the final pressure of the gas?
Answer:
Step 1: Rearrange the formula to change the conditions of a fixed amount of gas
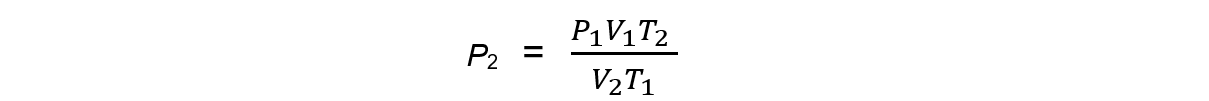
Step 2: Substitute in the values and calculate the final pressure
P1 = 80 kPa
V1 = 2.00 dm3
V2 = 2.25 dm3
T1 = 20 + 273 = 293 K
T2 = 70 + 273 = 343 K
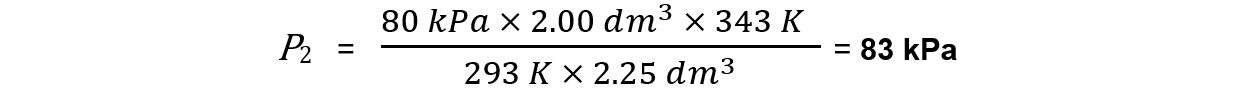
转载自savemyexams

最新发布
© 2026. All Rights Reserved. 沪ICP备2023009024号-1









