- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记11.3.3 Capacitors in Series & Parallel
Capacitors in Series & Parallel
- Capacitors can be combined in series and parallel circuits
- The combined capacitance depends on whether the capacitors are connected in series or parallel
Capacitors in Series
- Consider two parallel plate capacitors C1 and C2 connected in series, with a potential difference (p.d) V across them
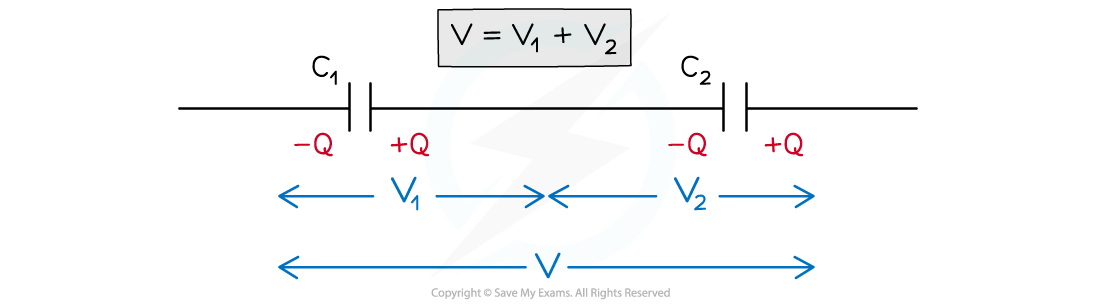
Capacitors connected in series have different p.d across them but have the same charge
- In a series circuit, p.d is shared between all the components in the circuit
- Therefore, if the capacitors store the same charge on their plates but have different p.ds, the p.d across C1 is V1 and across C2 is V2
- The total potential difference V is the sum of V1 and V2
V = V1 + V2
- Rearranging the capacitance equation for the p.d V means V1 and V2 can be written as:

- Where the total p.d V is defined by the total capacitance
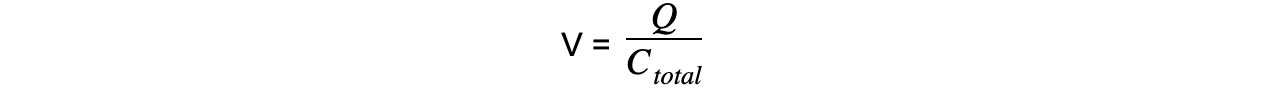
- Substituting these into the equation V = V1 + V2 equals:
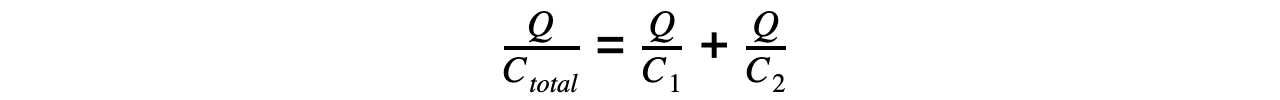
- Since the current is the same through all components in a series circuit, the charge Q is the same through each capacitor and cancels out
- Therefore, the equation for combined capacitance of capacitors in series is:
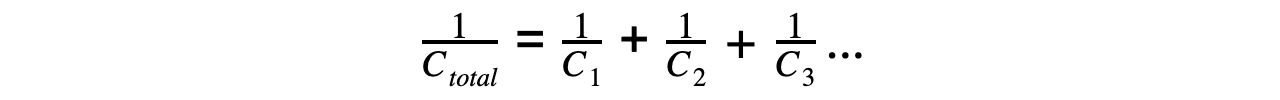
Capacitors in Parallel
- Consider two parallel plate capacitors C1 and C2 connected in parallel, each with p.d V

Capacitors connected in parallel have the same p.d across them, but different charge
- Since the current is split across each junction in a parallel circuit, the charge stored on each capacitor is different
- Therefore, the charge on capacitor C1 is Q1 and on C2 is Q2
- The total charge Q is the sum of Q1 and Q2
Q = Q1 + Q2
- Rearranging the capacitance equation for the charge Q means Q1 and Q2 can be written as:
Q1 = C1V and Q2 = C2V
- Where the total charge Q is defined by the total capacitance:
Q = CtotalV
- Substituting these into the Q = Q1 + Q2 equals:
CtotalV = C1V + C2V = (C1 + C2) V
- Since the p.d is the same through all components in each branch of a parallel circuit, the p.d V cancels out
- Therefore, the equation for combined capacitance of capacitors in parallel is:
Ctotal = C1 + C2 + C3 ...
Worked Example
Three capacitors with a capacitance of 23 μF, 35 μF and 40 μF are connected as shown below.

Calculate the total capacitance between points A and B.
Step 1: Calculate the combined capacitance of the two capacitors in parallel
Capacitors in parallel: Ctotal = C1 + C2 + C3 …
Cparallel = 23 + 35 = 58 μF
Step 2: Connect this combined capacitance with the final capacitor in series
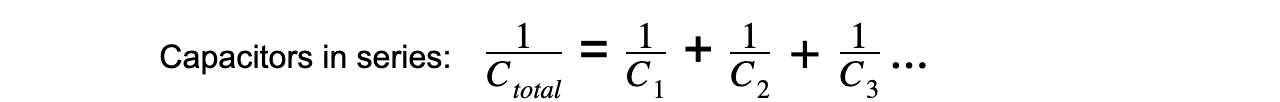
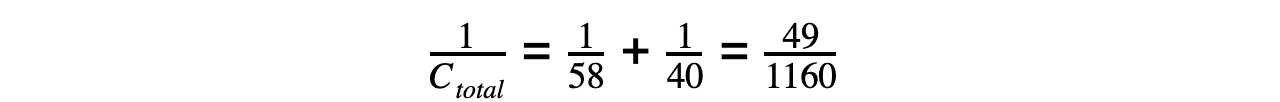
Step 3: Rearrange for the total capacitance
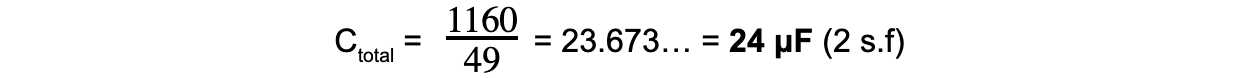
Exam Tip
You will be expected to remember these derivations for your exam, therefore, make sure you understand each step. You should especially make sure to revise how the current and potential difference varies in a series and parallel circuit.
Both the combined capacitance equations look similar to the equations for combined resistance in series and parallel circuits. However, take note that they are the opposite way around to each other!
转载自savemyexams

在线登记
最新发布
翰林课程体验,退费流程快速投诉邮箱: yuxi@linstitute.net 沪ICP备2023009024号-1








