IB DP Physics: HL复习笔记10.2.1 Potential & Potential Energy
Potential & Potential Energy
Work Done on a Mass
- When a mass is moved against the force of gravity, work is done
- The work done in moving a mass m is given by:
- Where:
- ∆W = change in work done (J)
- m = mass (kg)
- ∆V = change in gravitational potential (J kg-1)
- This change in work done is equal to the change in gravitational potential energy (G.P.E)
-
- When V = 0, then the G.P.E = 0
- The change in G.P.E, or work done, for an object of mass m at a distance r1 from the centre of a larger mass M, to a distance of r2 further away can be written as:
-
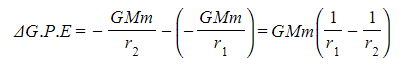Where:
- M = mass that is producing the gravitational field (eg. a planet) (kg)
- m = mass that is moving in the gravitational field (eg. a satellite) (kg)
- r1 = first distance of m from the centre of M (m)
- r2 = second distance of m from the centre of M (m)
- Work is done when an object in a planet's gravitational field moves against the gravitational field lines i.e.: away from the planet
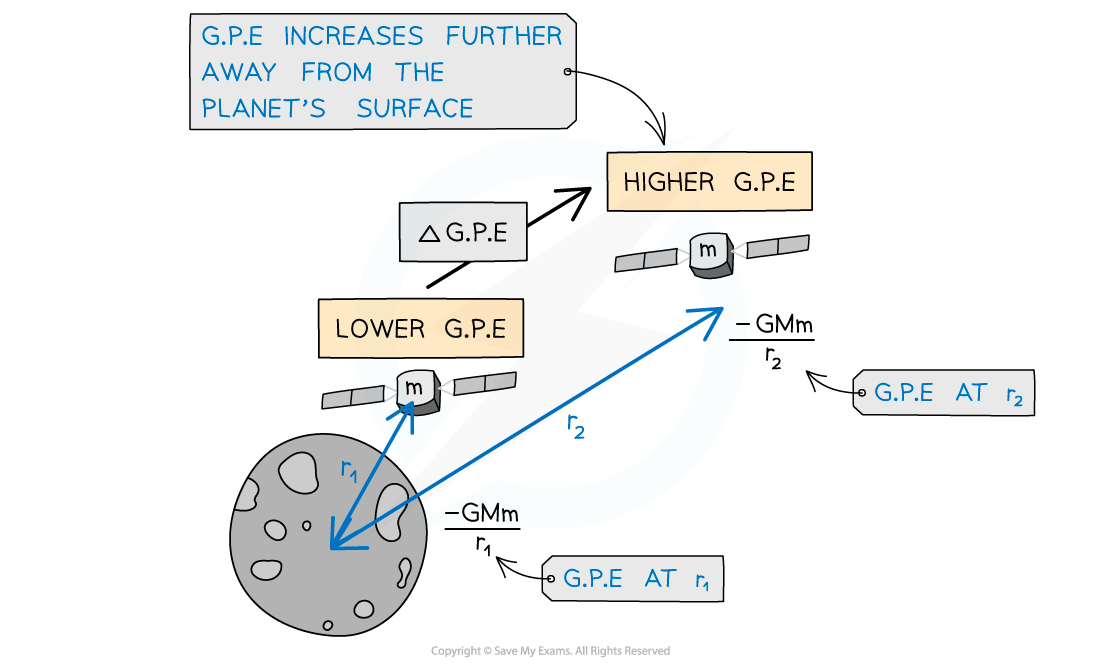
Gravitational potential energy increases as a satellite leaves the surface of the Moon
Worked Example
A spacecraft of mass 300 kg leaves the surface of Mars to an altitude of 700 km. Calculate the work done by the spacecraft. The radius of Mars = 3400 km, Mass of Mars = 6.40 × 1023 kg
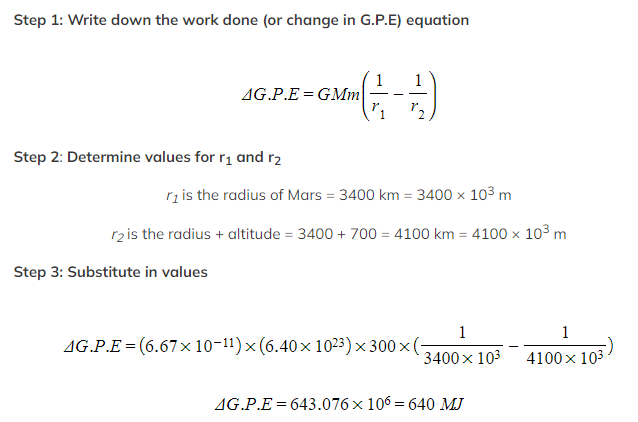Work Done on a Charge
- When a mass with charge moves through an electric field, work is done
- The work done in moving a charge q is given by:
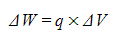Where:
- ∆W = change in work done (J)
- q = charge (C)
- ∆V = change in electric potential (J C-1)
- This change in work done is equal to the change in electric potential energy (E.P.E)
- When V = 0, then the E.P.E = 0
- The change in E.P.E, or work done, for a point charge q at a distance r1 from the centre of a larger charge Q, to a distance of r2 further away can be written as:
-
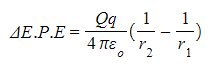Where:
- Q = charge that is producing the electric field (C)
- q = charge that is moving in the electric field (C)
- r1 = first distance of q from the centre of Q (m)
- r2 = second distance of q from the centre of Q (m)
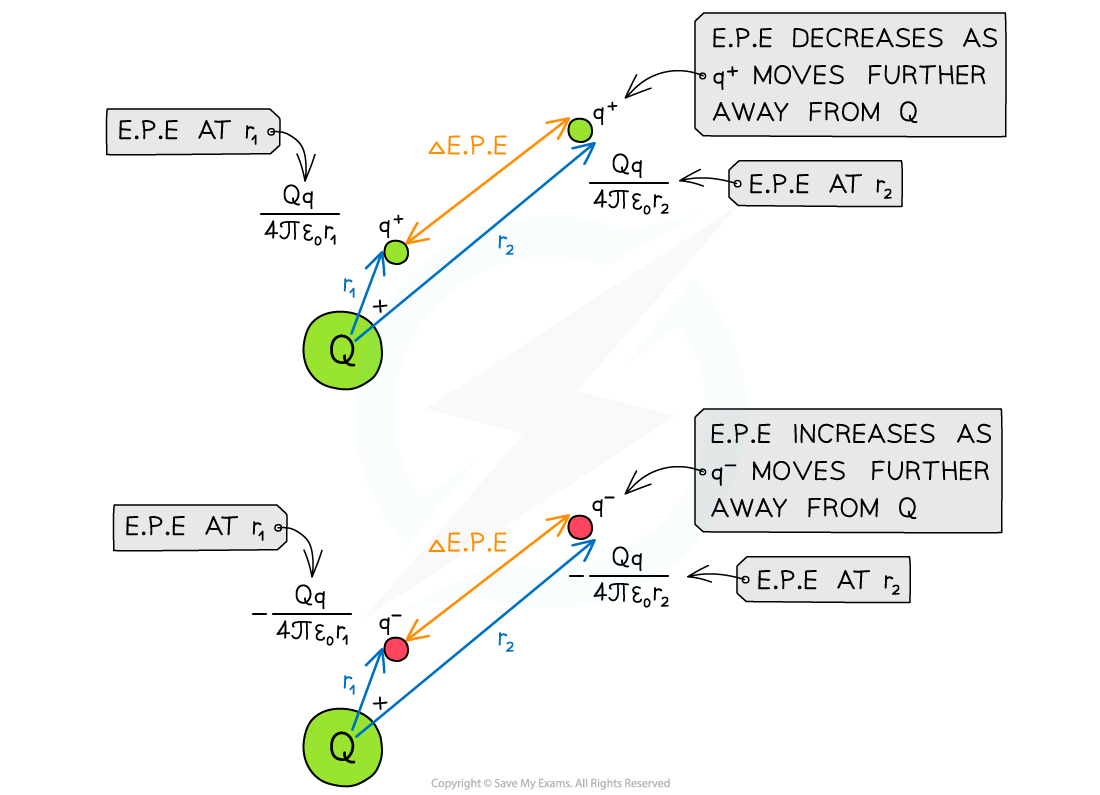
Work is done when moving a point charge away from another charge
- Work is done when a positive charge in an electric field moves against the electric field lines or when a negative charge moves with the electric field lines
Worked Example
The potentials at points R and S due to the +7.0 nC charge are 675 V and 850 V respectively.
Calculate how much work is done when a +3.0 nC charge is moved from R to S.
Step 1: Write down the known quantities
-
- p.d. at R, V1 = 675 V
- p.d. at S, V2 = 850 V
- Charge, q = +3.0 nC = +3.0 × 10-9 C
Step 2: Write down the work done equation
W = q × ΔV
Step 3: Substitute in the values into the equation
W = (3.0 × 10-9) × (850 - 675) = 5.3 × 10-7 J
Exam Tip
Make sure to not confuse the ΔG.P.E equation with ΔG.P.E = mgΔh, they look similar but refer to quite different situations.
The more familiar equation is only relevant for an object lifted in a uniform gravitational field, meaning very close to the Earth’s surface, where we can model the field as uniform.
The new equation for G.P.E does not include g. The gravitational field strength, which is different on different planets, does not remain constant as the distance from the surface increases. Gravitational field strength falls away according to the inverse square law.
Remember that q in the work done equation is the charge that is being moved, whilst Q is the charge which is producing the potential. Make sure not to get these two mixed up. It is common for both to be given in the question, as in our worked example. You are expected to choose the correct one.
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
AMC8备考管家服务全新上线！
