- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记9.1.4 Examples of SHM
Period of a Simple Pendulum & a Mass-Spring System
- Two examples of simple harmonic oscillators are:
- A simple pendulum
- A mass-spring system
- Considering equations related to the restoring force leads to expressions for the time periods of these scenarios
- These relationships are useful for investigating simple harmonic motion experimentally
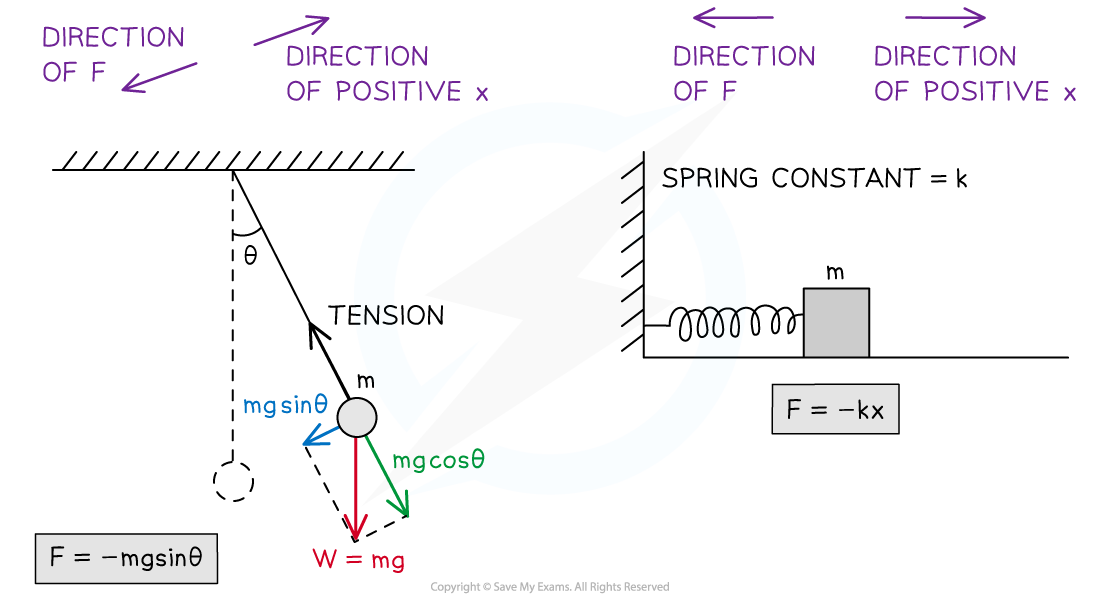
For a pendulum, the restoring force is provided by the component of the bob's weight that is perpendicular to the tension in the pendulum's string. For a mass-spring system, the restoring force is provided by the force of the spring
Time Period of a Simple Pendulum
- A simple pendulum is a type of simple harmonic oscillator
- The pendulum consists of a string and a bob (a weight, generally spherical) at the end
- An oscillating pendulum can be modelled as simple harmonic motion when the angle of oscillation is small

Forces on a pendulum when it is displaced. Assuming θ < 10°, the small angle approximation can be used to describe the time period of a simple pendulum such as this.
- The restoring force, F, which returns an oscillating pendulum bob to the equilibrium position is:
F = −mg sin θ
- Where:
- m = the mass of the pendulum bob (kg)
- g = acceleration due to gravity (m s−2)
- θ = angle between the bob and the vertical (°)
- Using Newton’s Second Law:
F = ma = −mg sin θ
- Both sides can be divided by m to give an expression for the acceleration, a:
a = −g sin θ
- In this case, the small-angle approximation can be used, this is where sin θ ≅ θ
- This is assuming the angle the pendulum makes with the vertical is less than 10°
- The expression for acceleration then becomes:
a = −gθ
- The displacement, x, is equal to the length of the arc made by the bob, x = Lθ
- Where L = length of the pendulum (m)
- Rearranging this for θ and substituting it into the acceleration equation gives:
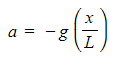 This equation shows:
This equation shows:
- For small values of x, the condition for SHM is satisfied as restoring force, F is proportional to −x
- For large values of x, the acceleration of a simple pendulum is not proportional to the displacement
- Using the defining equation of SHM:

Time Period of a Mass–Spring System
- A mass-spring system is another type of simple harmonic oscillator
- The restoring force, F, which returns a mass-spring system to its equilibrium position is given by:
F = −kx
-
- x = extension of the spring (m)
- k = spring constant (N m−1)Where:
- Using Newton’s Second Law:
F = ma = −kx
- Rearranging for the acceleration, a:

- This equation applies for both a horizontal or vertical mass-spring system

A mass-spring system can be either vertical or horizontal. The time period equation applies to both.
- The equation shows that:
- The higher the spring constant k, the stiffer the spring and hence, the shorter the time period of oscillation
- The time period (and hence, frequency) of a mass-spring system is independent of the force of gravity
- A consequence of this is that oscillations would have the same time period on Earth and the Moon
Worked Example
A swinging pendulum with a length of 80.0 cm has a maximum angle of displacement of 8°.
Determine the angular frequency of the oscillation.
Step 1: List the known quantities
-
- Length of the pendulum, L = 80 cm = 0.8 m
- Acceleration due to gravity, g = 9.81 m s−2
Step 2: Write down the relationship between angular frequency, ω, and period, T
Step 3: Write down the equation for the time period of a simple pendulum
-
- This equation is valid for this scenario since the maximum angle of displacement is less than 10°
Step 4: Equate the two equations and rearrange for ω
Step 5: Substitute the values to calculate ω
= 3.50 rad s−1
Step 6: State the final answer to the correct number of significant figures
ω = 3.5 rad s−1
Worked Example
Calculate the frequency of a mass of 2.0 kg attached to a spring with a spring constant of 0.9 N m–1 oscillating with simple harmonic motion.
Step 1: Write down the known quantities
-
- Mass, m = 2.0 kg
- Spring constant, k = 0.9 N m−1

Exam Tip
Another area of physics where you may have seen the spring constant k is in Hooke's Law, where F = kx.
Exam questions commonly merge these topics together, so make sure you're familiar with the Hooke's Law equation too.
The motion of both pendula and mass-spring systems can be described in graphical and mathematical forms. As with other forms of motion, you should become familiar with both
Make sure to pay particular attention to the difference between the graph shapes produced when the oscillator starts at the equilibrium position or maximum displacement
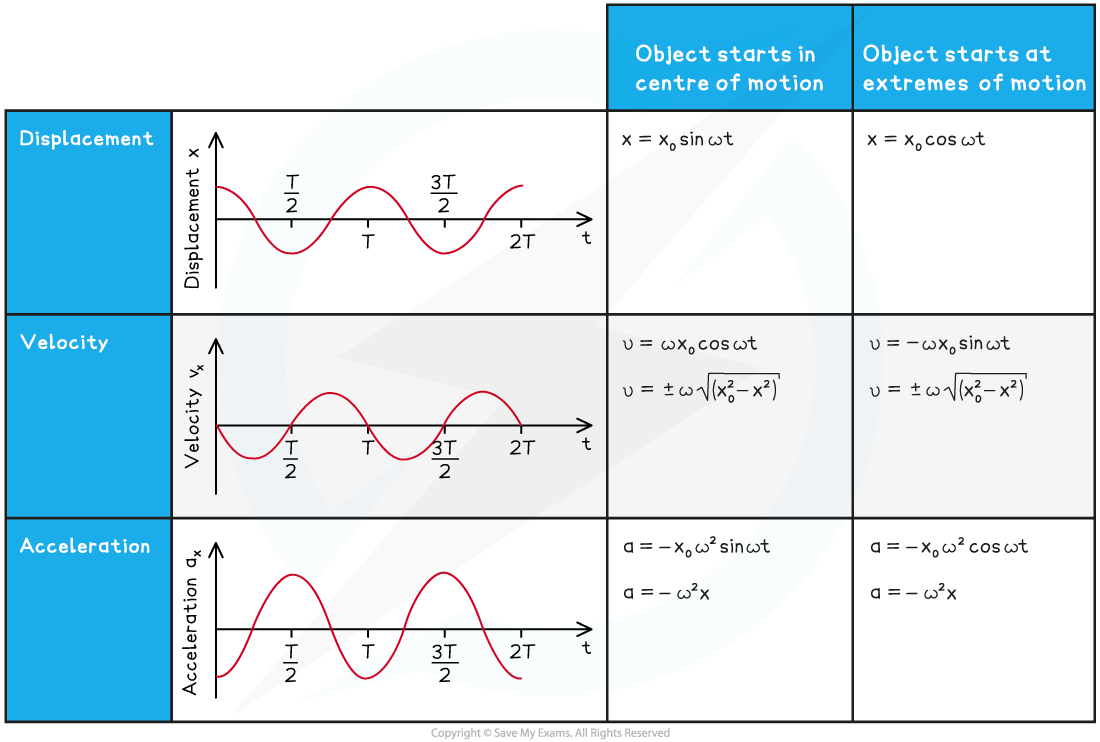
Graphs and equations can be used to describe different aspects of oscillations
转载自savemyexams

最新发布
© 2026. All Rights Reserved. 沪ICP备2023009024号-1









