- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记9.1.3 Calculating Energy Changes in SHM
Calculating Energy Changes in SHM
- There are many equations to learn in the topic of simple harmonic motion
- The key equations are summarised below:
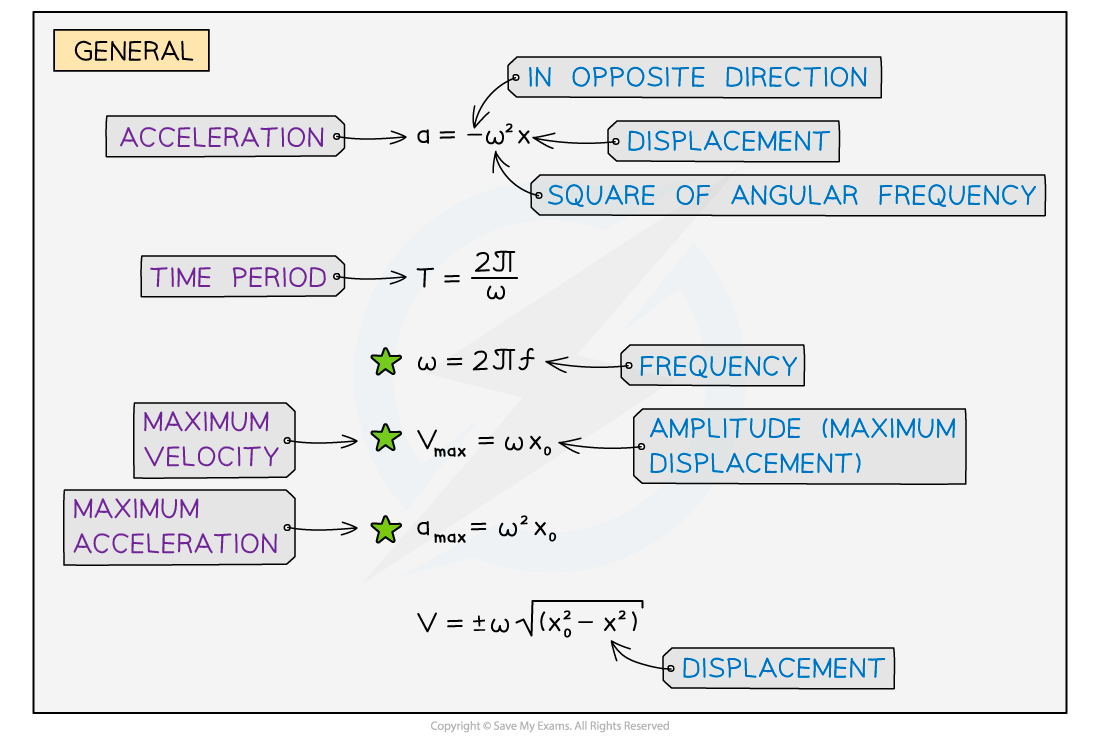
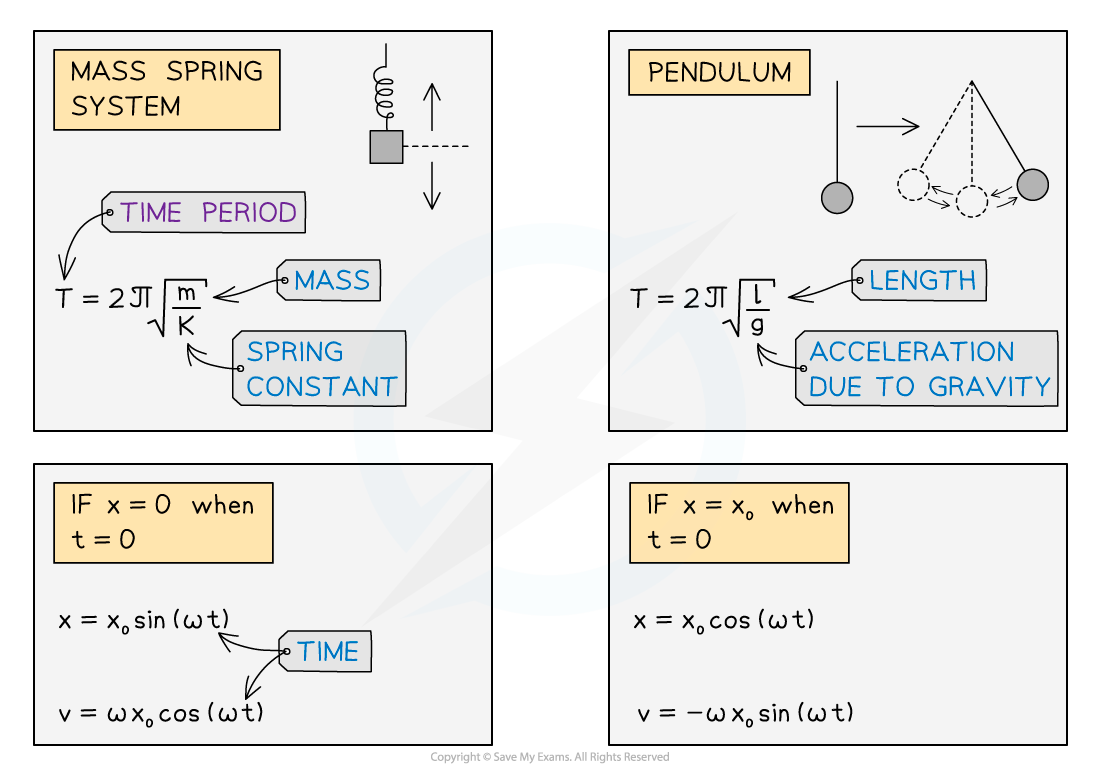
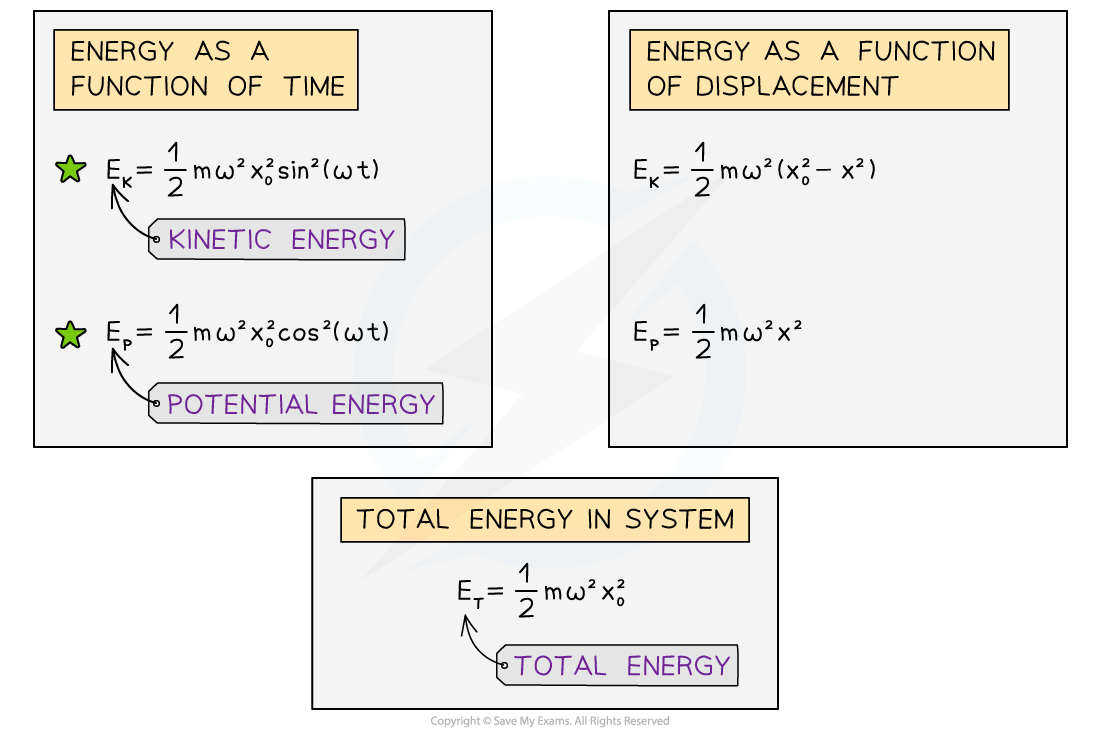
A summary of the equations related to simple harmonic motion. The green stars indicate equations which are not included in the IB data booklet
Worked Example
The graph shows the potential energy, EP, for a particle oscillating with SHM. The particle has mass 45 g.

Part (a)
Step 1: List the known quantities
-
-
- Mass of the particle, m = 45 g = 45 × 10−3 kg
-
Step 2: Use the graph to determine the maximum potential energy of the particle
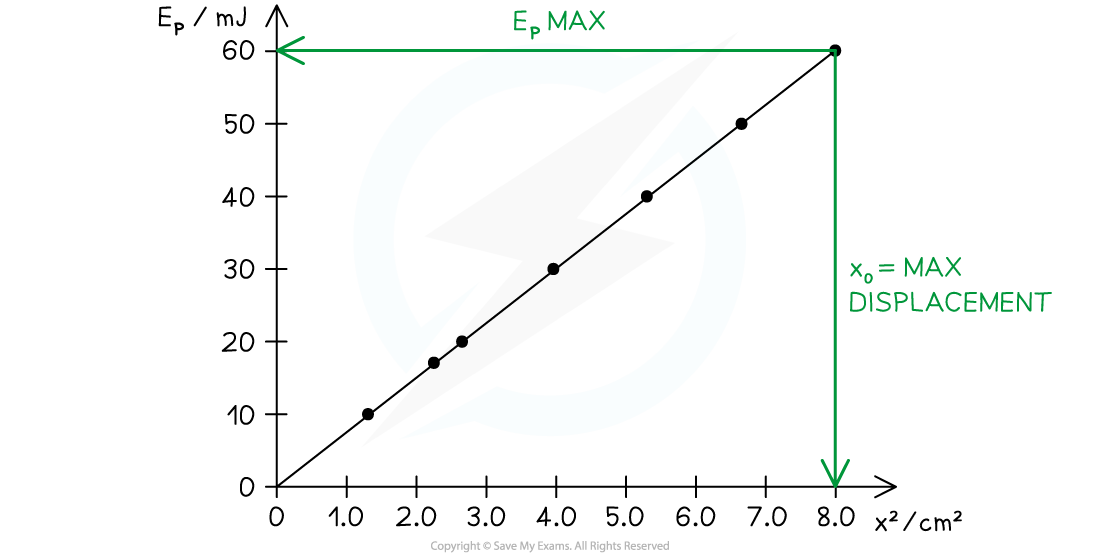
-
-
- Maximum potential energy, EPmax = 60 mJ = 60 × 10−3 J
-
Step 3: Determine the amplitude of the oscillation
-
-
- The amplitude of the motion, x0, is the maximum displacement
- At the maximum displacement, the particle is at its highest point, hence this is the position of maximum potential energy
- From the graph, when EP = EPmax:
-
x02 = 8.0 cm = 0.08 m
-
-
- Therefore, the amplitude is:
-
x0 = √0.08 = 0.28 m
Step 4: Write down the equation for the potential energy of an oscillator
Part (b)
Step 1: List the known quantities
-
-
- Angular velocity, ω = 5.77 rad s−1
- Amplitude, x0 = 0.28 m
-
Step 2: Write down the equation for the maximum speed of an oscillator
vmax = ωx0
Step 3: Substitute in the known quantities
vmax = 5.77 × 0.28 = 1.6 m s−1
Worked Example
A student investigated the behaviour of a 200 g mass oscillating on a spring, and produced the graph shown.
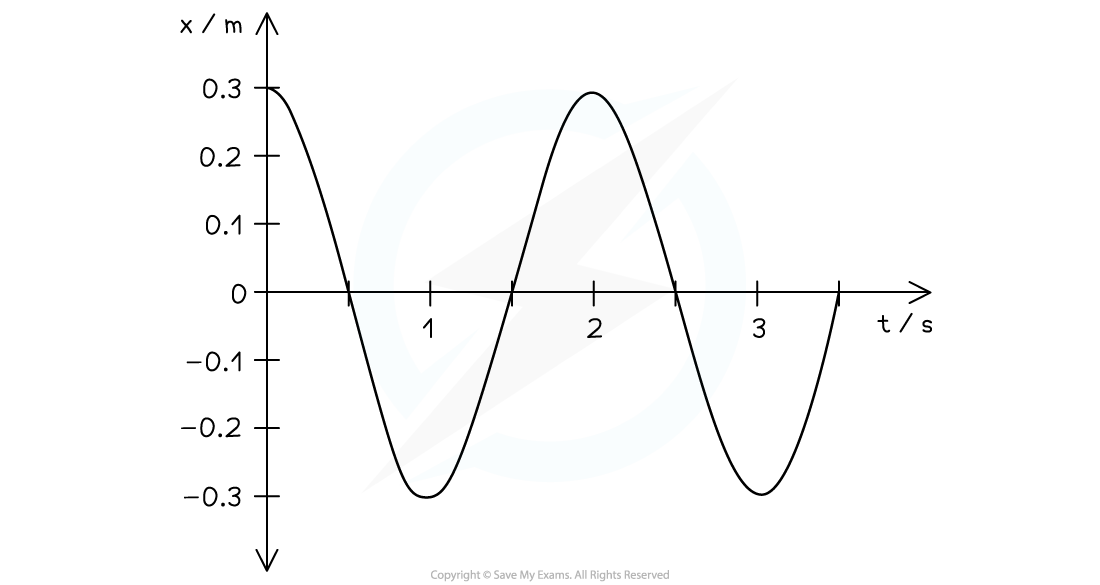
Part (a)
Step 1: Read the values of amplitude and time period from the graph
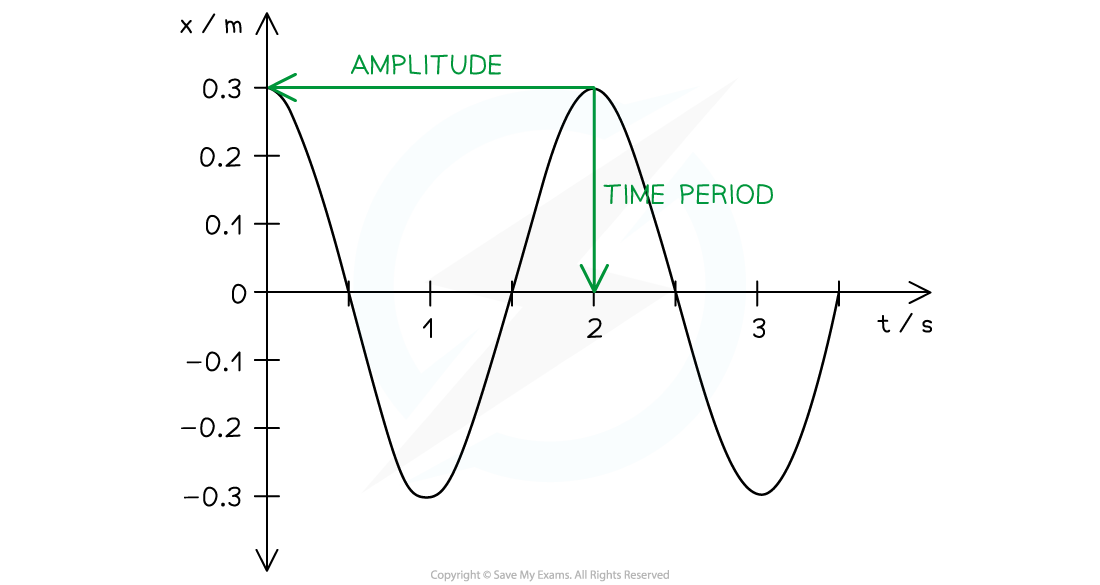
Step 2: State the values of amplitude and time period
-
-
- Amplitude, x0 = 0.3 m
- Time period, T = 2.0 s
-
Part (b)
Step 1: List the known quantities
-
-
- Mass of the oscillator, m = 200 g = 0.2 kg
-
Step 2: Write down the equation for the maximum speed of an oscillator
vmax = ωx0
Step 3: Write down the equation relating angular speed and time period
Worked Example
A ball of mass 23 g is held between two fixed points A and B by two stretch helical springs, as shown in the diagram below.
 The ball oscillates along the line AB with simple harmonic motion of frequency 4.8 Hz and amplitude 1.5 cm.
The ball oscillates along the line AB with simple harmonic motion of frequency 4.8 Hz and amplitude 1.5 cm.
Calculate the total energy of the oscillations.
Step 1: Write down all known quantities
-
- Mass, m = 23 g = 23 × 10–3 kg
- Amplitude, x0 = 1.5 cm = 0.015 m
- Frequency, f = 4.8 Hz
Step 2: Write down the equation for the total energy of SHM oscillations:
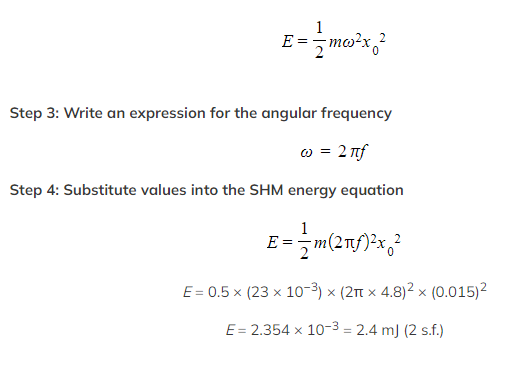
Exam Tip
There are a large number of equations associated with SHM. Most of them are given in the data booklet which you will be given to use in the exam
Make sure you are familiar with the equations, as you will probably need to use several different ones to solve the longer questions.
转载自savemyexams

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









