IB DP Physics: HL复习笔记9.1.1 The Defining Equation of SHM

• Simple harmonic motion (SHM) is a fundamental oscillation which appears naturally in various phenomena, including:
  • The swing of a pendulum
  • A mass on a spring
  • Guitar strings
  • Vibrations of molecules

• SHM is defined as:

A type of oscillation in which the acceleration on a body is proportional to its displacement, but acts in the opposite direction

• The conditions for an object to oscillate in SHM are that it shows:
  • Periodic oscillations
  • Acceleration proportional to its displacement
  • Acceleration in the opposite direction to its displacement

• SHM is isochronous, meaning that the time period stays constant
  • Therefore frequency must also be constant
• The period of simple harmonic oscillations can be calculated using the equation:

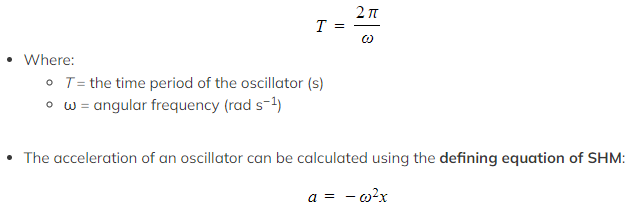
• Where:
  • a = acceleration of the oscillator (m s−2)
  • x = displacement of the oscillator from its equilibrium position (m)

• The equation shows that:
  • The acceleration reaches its maximum value when the displacement is at a maximum i.e. x = x0
  • The minus sign shows that when the object is displacement to the right, the direction of the acceleration is to the left

• An object in SHM will have a restoring force acting on it to return it to its equilibrium position
• This restoring force will be directly proportional, but in the opposite direction, to the displacement of the object from the equilibrium position
  • Note: the restoring force and acceleration act in the same direction

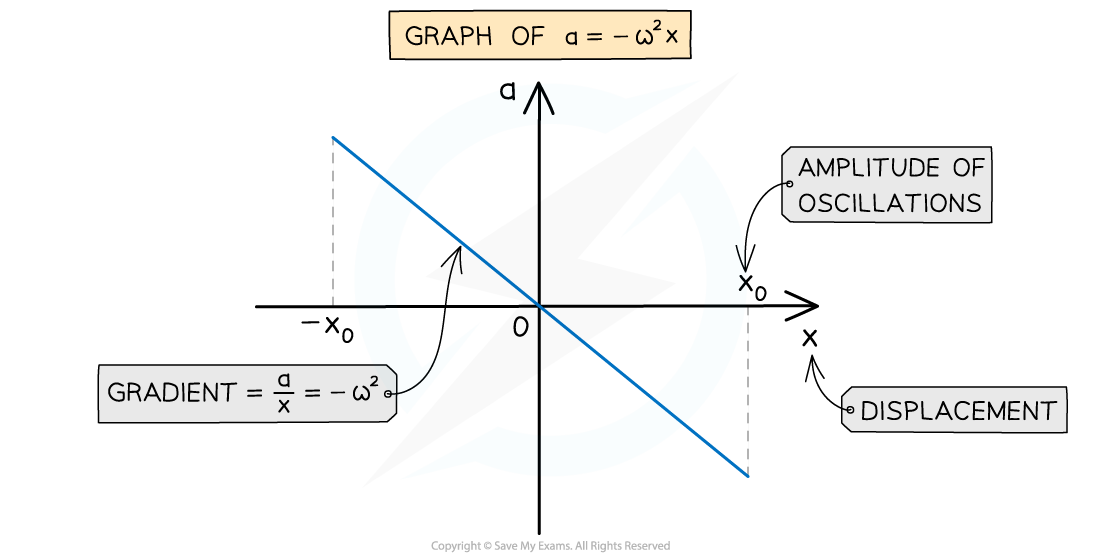
The acceleration of an object in SHM is directly proportional to the negative displacement

Calculating Displacement of an Oscillator

• The graph of acceleration against displacement is a straight line through the origin sloping downwards (similar to y = −x)
• Key features of the graph:
  • The gradient is equal to −ω2
  • The maximum and minimum displacement x values are the amplitudes −x0 and +x0
• A solution to the SHM acceleration equation is the displacement equation:

• This is because the cosine graph starts at a maximum, whilst the sine graph starts at 0

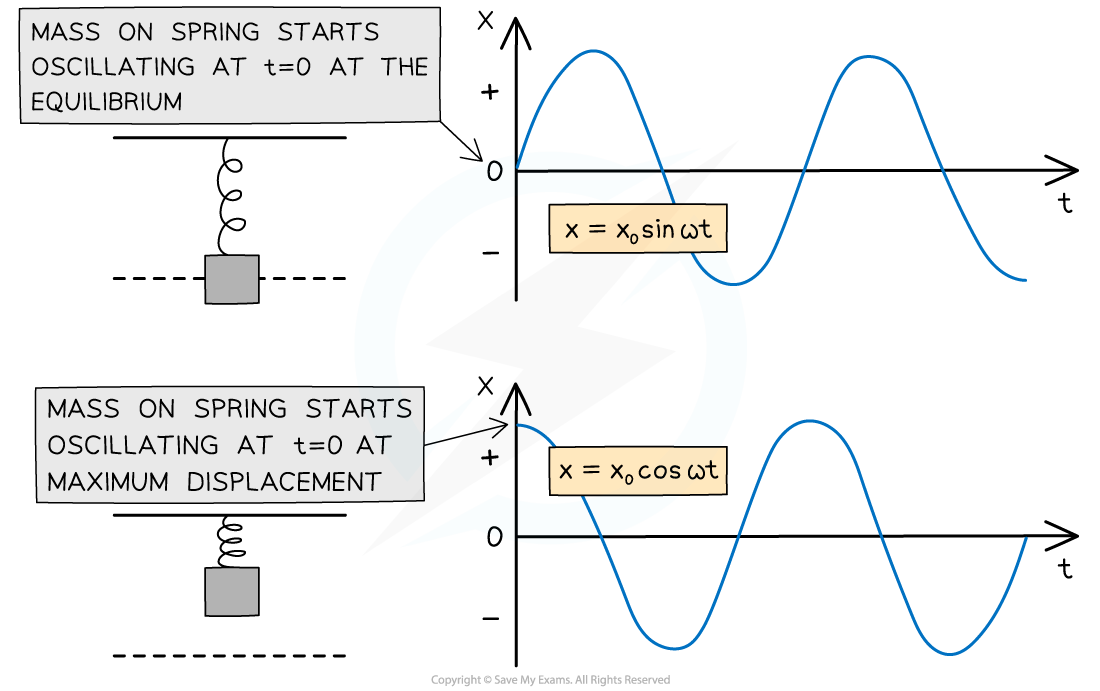
These two graphs represent the same SHM. The difference is the starting position

Equations & Graphs for SHM

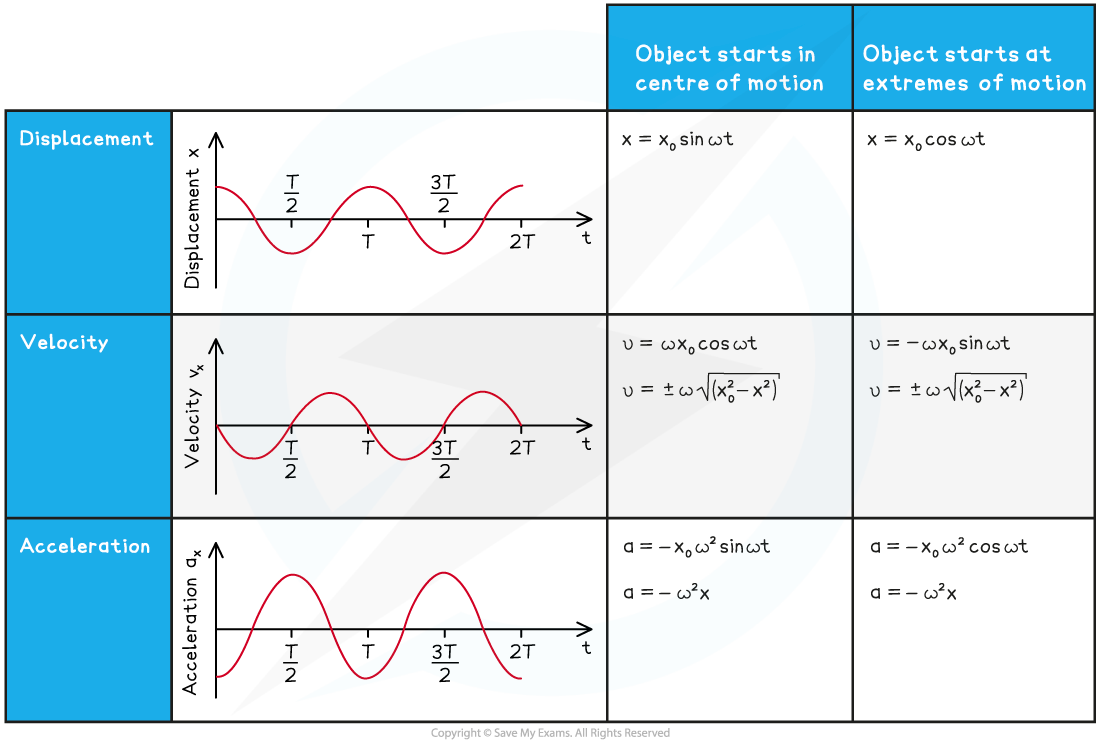
• A summary of the equations and graphs of simple harmonic motion are shown in the table
• Note that the equations differ depending on the starting point of the oscillator
  • The derivation of these equations are found lower down the page

Summary table of equations and graphs for displacement, velocity and acceleration

Step 1: List the known quantities

• • Maximum displacement, x0 = 4.3 cm
  • Period of oscillation, T = 0.8 s
  • Time interval, t = 0.3 s

Step 2: Write down the SHM displacement equation

• • Since the mass is released at t = 0 at its maximum displacement, the displacement equation will involve the cosine function:

• • The negative value means the mass is 3.0 cm on the opposite side of the equilibrium position to where it started i.e. 3.0 cm above it

Calculating Velocity of an Oscillator

• The velocity, v, of an oscillation can be found by differentiating the displacement with respect to time::

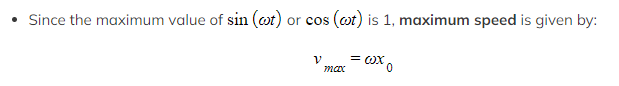
Calculating Acceleration of an Oscillator

• The acceleration, a, of an oscillator can be found by differentiating the displacement with respect to time twice:

• This is the maximum acceleration of the oscillator regardless of its starting point

Displacement–Velocity Relation for SHM

• A useful relation between the displacement and velocity of a simple harmonic oscillator can be derived using the expressions from the equilibrium position: