- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Physics: HL复习笔记2.1.5 Uniform Acceleration
Equations of Motion for Uniform Acceleration
Deriving Kinematic Equations of Motion
- The kinematic equations of motion are a set of four equations that can describe any object moving with constant acceleration
- They relate the five variables:
- s = displacement
- u = initial velocity
- v = final velocity
- a = acceleration
- t = time interval
- Knowing where these equations come from and how they are derived helps understand them:
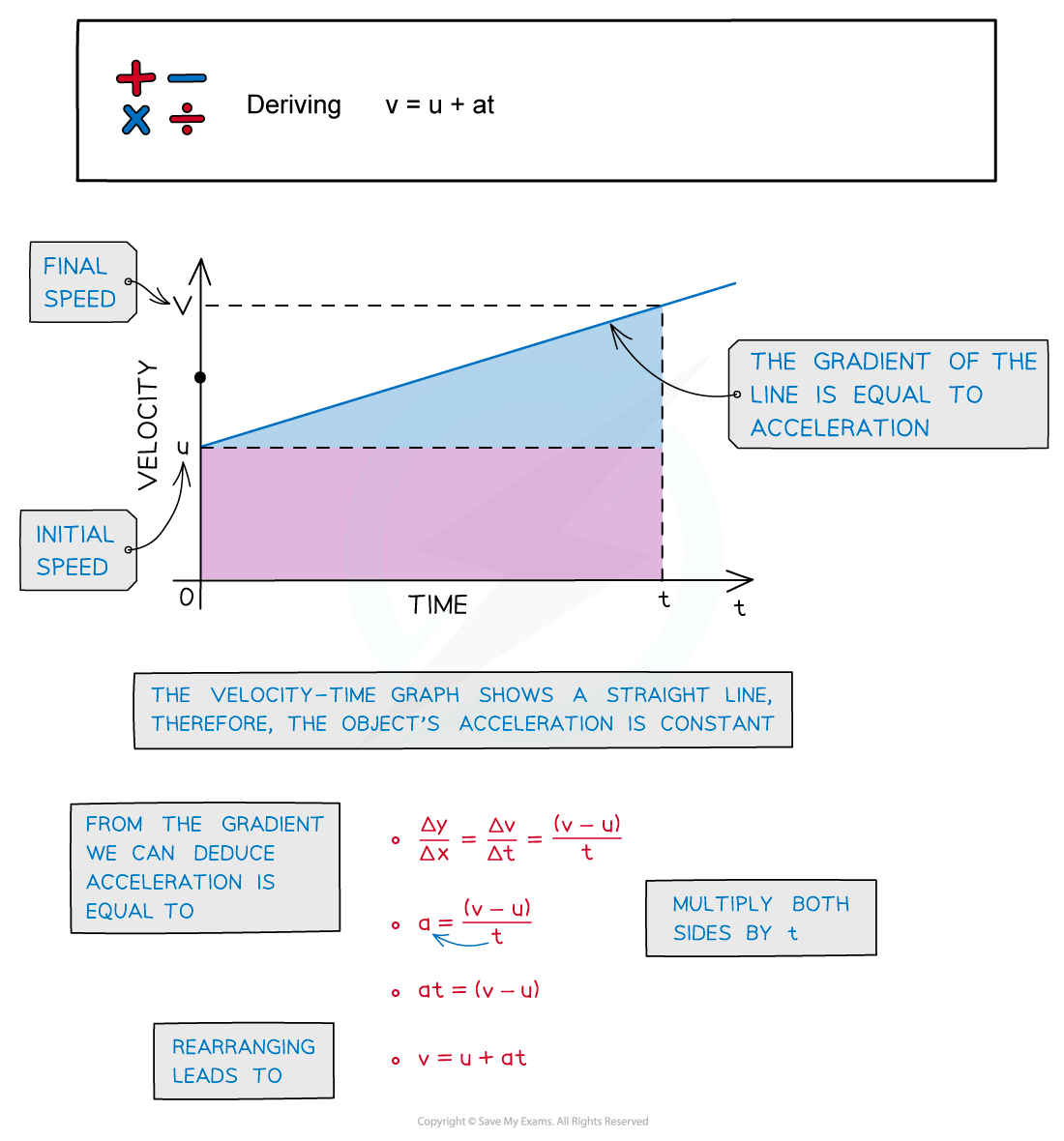
A graph showing how the velocity of an object varies with time

The average velocity is halfway between u and v
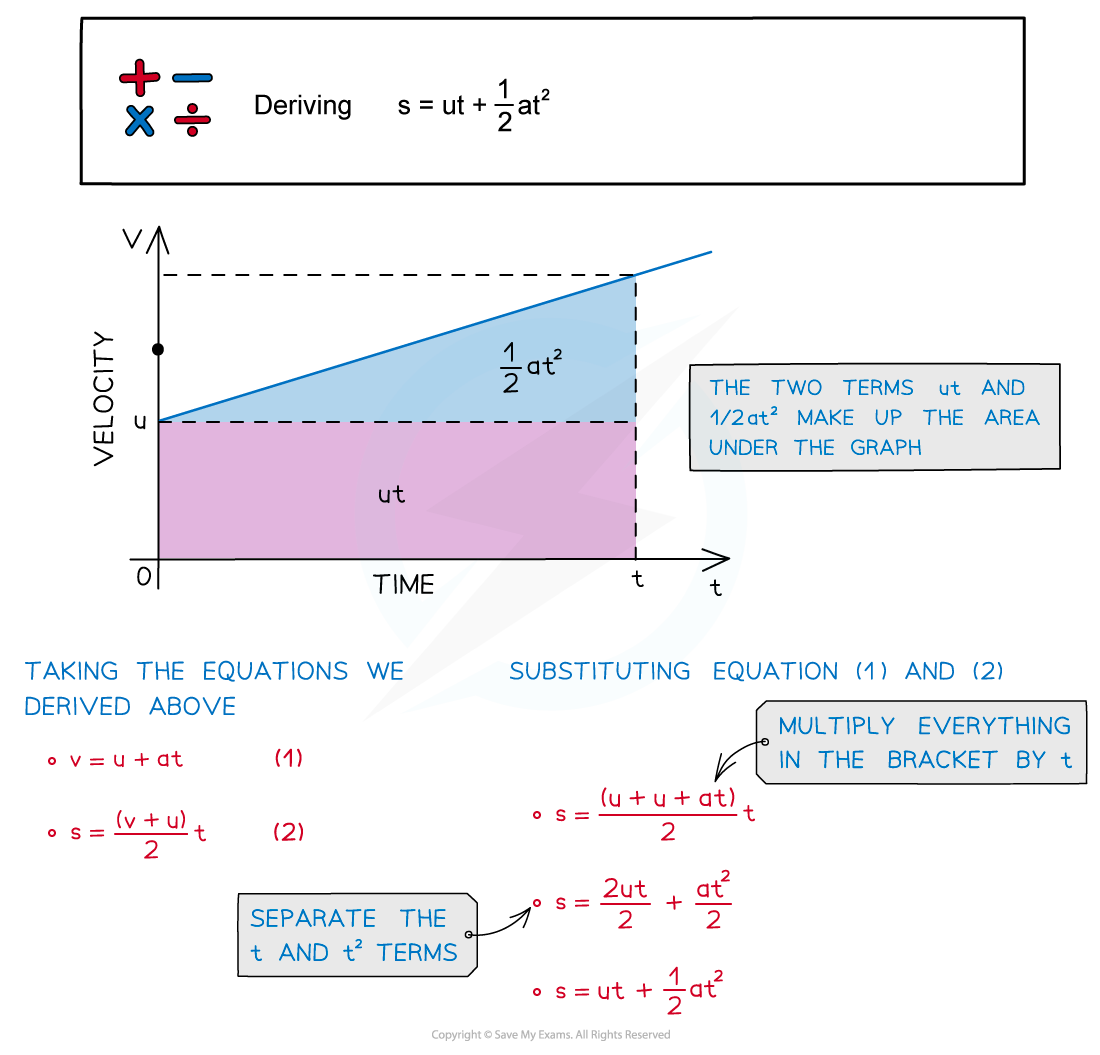
The two terms ut and ½at2 make up the area under the graph
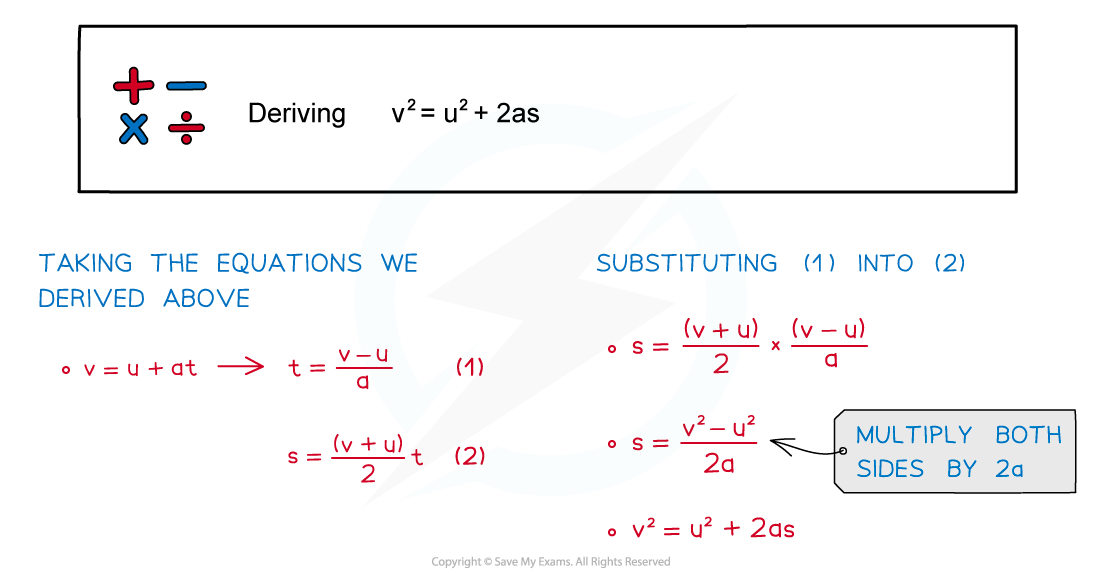
This final equation can be derived from two of the others

Summary of the four equations of uniformly accelerated motion
Key Takeaways
- These are all given in the IB DP Physics data booklet
- The key terms to look out for are:
'Starts from rest',
- This means u = 0 and t = 0
- This can also be assumed if the initial velocity is not mentioned
'Falling due to gravity'
- This means a = g = 9.81 m s–2
- It doesn't matter which way is positive or negative for the scenario, as long as it is consistent for all the vector quantities
- For example, if downwards is negative then for a ball travelling upwards, s must be positive and a must be negative
'Constant acceleration in a straight line'
- This is a key indication SUVAT equations are intended to be used
- For example, an object falling in a uniform gravitational field without air resistance
How to use the SUVAT equations
- Step 1: Write out the variables that are given in the question, both known and unknown, and use the context of the question to deduce any quantities that aren’t explicitly given
- e.g. for vertical motion a = ± 9.81 m s–2, an object which starts or finishes at rest will have u = 0 or v = 0
- Step 2: Choose the equation which contains the quantities you have listed
- e.g. the equation that links s, u, a and t is s = ut + ½at2
- Step 3: Convert any units to SI units and then insert the quantities into the equation and rearrange algebraically to determine the answer
Worked Example
The diagram shows an arrangement to stop trains that are travelling too fast.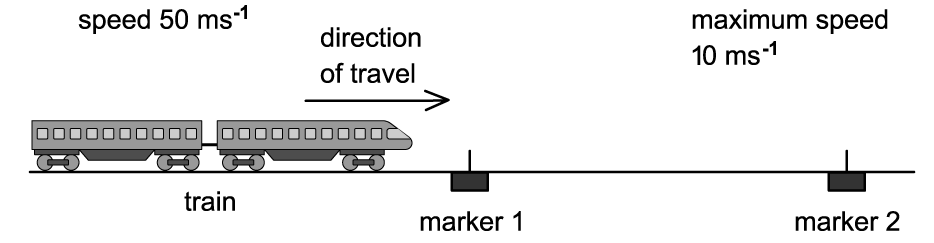 At marker 1, the driver must apply the brakes so that the train decelerates uniformly in order to pass marker 2 at no more than 10 m s–1.The train carries a detector that notes the times when the train passes each marker and will apply an emergency brake if the time between passing marker 1 and marker 2 is less than 20 s.Trains coming from the left travel at a speed of 50 m s–1.Determine how far marker 1 should be placed from marker 2.
At marker 1, the driver must apply the brakes so that the train decelerates uniformly in order to pass marker 2 at no more than 10 m s–1.The train carries a detector that notes the times when the train passes each marker and will apply an emergency brake if the time between passing marker 1 and marker 2 is less than 20 s.Trains coming from the left travel at a speed of 50 m s–1.Determine how far marker 1 should be placed from marker 2.

Worked Example
A cyclist is travelling directly east through a village, which is completely flat, at a velocity of 6 m s–1 east. They then start to constantly accelerate at 2 m s–2 for 4 seconds.
a) Calculate the distance that the cyclist covers in the 4 second acceleration period.
b) Calculate the cyclist's final velocity after the 4-second interval of acceleration.
Later on in their journey, this cyclist (cyclist A) is now cycling through a different village, still heading east at a constant velocity of 18 m s–1. Cyclist A passes a friend (cyclist B) who begins accelerating from rest at a constant acceleration of 1.5 m s–2 in the same direction as cyclist A at the moment they pass.
c) Calculate how long it takes for cyclist B to catch up to cyclist A.
Part (a)
Step 1: List the known quantities
-
-
- Initial velocity, u = 6 m s–1 East
- Acceleration, a = 2 m s–2 East
- Time, t = 4 s
- Displacement, s = ? (this needs to be calculated)
-
Step 2: Identify and write down the equation to use
-
-
- Since the question states constant acceleration, SUVAT equations can be used
- In this problem, the equation that links s, u, a, and t is
-
s = (u × t) + (½ × a × t2)
Step 3: Substitute known quantities into the equation and simplify where possible
s = (6 × 4) + (0.5 × 2 × 42)
-
-
- This can be simplified to:
-
s = 24 + 16 = 40 m
Part (b)
Step 1: List the known quantities
-
-
- Initial velocity, u = 6 m s–1 East
- Acceleration, a = 2 m s–2 East
- Time, t = 4 s
- final velocity, v = ? (this needs to be calculated)
-
Step 2: Identify and write down the equation to use
-
-
- Since the question states constant acceleration - SUVAT equation(s) - can be used
- In this problem, the equation that links v, u, a, and t is v = u + (a × t)
-
Step 3: Substitute known quantities into the equation and simplify where possible
v = 6 + (2 × 4)
-
-
- This can be simplified to:
-
v = 14 m s–1
Part (c)
Step 1: List the known quantities for cyclist A
-
-
- Initial velocity, u = 18 m s–1 East
- Acceleration, a = 0 m s–2 East
- Final velocity, v = 18 m s–1 East
- Time, t = ?
- Displacement, s = ?
-
Step 2: List the known quantities for cyclist B
-
-
- Initial velocity, u = 0 m s–1 East
- Acceleration, a = 1.5 m s–2 East
- Final velocity, v = ?
- Time, t = ?
- Displacement, s = ?
-
Step 3: Express the situation for cyclist A and B in terms of displacement, s
-
-
- Cyclist A can have their situation expressed by:
-
sA = (u × t) + (½ × a × t2)
sA = (18 × t) + (½ × 0 × t2) = (18 × t)
-
-
- Cyclist B can have their situation expressed by:
-
sB = (u × t) + (½ × a × t2)
sB = (0 × t) + (½ × 1.5 × t2) = (0.75 × t2)
Step 4: Equate the two equations and solve for t
-
-
- The two equations describe the displacement of each cyclist respectively
- When equating them, this will find the time when the cyclists are at the same location
-
sA= sB = (18 × t) = (0.75 × t2)
0 = (0.75 × t2) – (18 × t)
0 = (0.75 × t – 18) × t
-
-
- Therefore, solving for t, it can be two possible answers:
-
t = 0 s or 18 / 0.75 = 24 s
Step 4: State the final answer
-
-
- Since the question is seeking the time when the two cyclists meet after first passing each other, the final answer is 24 s
-
Exam Tip
This is one of the most important sections of this topic - usually, there will be one, or more, questions in the exam about solving problems with SUVAT equationsThe best way to master this section is to practice as many questions as possible!
转载自savemyexams

最新发布
© 2026. All Rights Reserved. 沪ICP备2023009024号-1









