IB DP Chemistry: HL复习笔记15.1.3 Born-Haber Cycle Calculations

• Once a Born-Haber cycle has been constructed, it is possible to calculate the lattice energy (ΔH_lat^ꝋ) by applying Hess’s law and rearranging:

ΔH_f^ꝋ = ΔH_at^ꝋ + ΔH_at^ꝋ + IE + EA + ΔH_lat^ꝋ

• If we simplify this into three terms, this makes the equation easier to see:
  • ΔH_lat^ꝋ
  • ΔH_f^ꝋ
  • ΔH₁^ꝋ (the sum of all of the various enthalpy changes necessary to convert the elements in their standard states to gaseous ions)
• The simplified equation becomes:

ΔH_f^ꝋ = ΔH₁^ꝋ + ΔH_lat^ꝋ

• So, if we rearrange to calculate the lattice energy, the equation becomes

ΔH_lat^ꝋ = ΔH_f^ꝋ - ΔH₁^ꝋ

• When calculating the ΔH_lat^ꝋ, all other necessary values will be given in the question
• A Born-Haber cycle could be used to calculate any stage in the cycle
  • For example, you could be given the lattice energy and asked to calculate the enthalpy change of formation of the ionic compound
  • The principle would be exactly the same
  • Work out the direct and indirect route of the cycle (the stage that you are being asked to calculate will always be the direct route)
  • Write out the equation in terms of enthalpy changes and rearrange if necessary to calculate the required value
• Remember: sometimes a value may need to be doubled or halved, depending on the ionic solid involved
  • For example, with MgCl₂ the value for the first electron affinity of chlorine would need to be doubled in the calculation, because there are two moles of chlorine atoms
  • Therefore, you are adding 2 moles of electrons to 2 moles of chlorine atoms, to form 2 moles of chloride ions, i.e. 2Cl^-

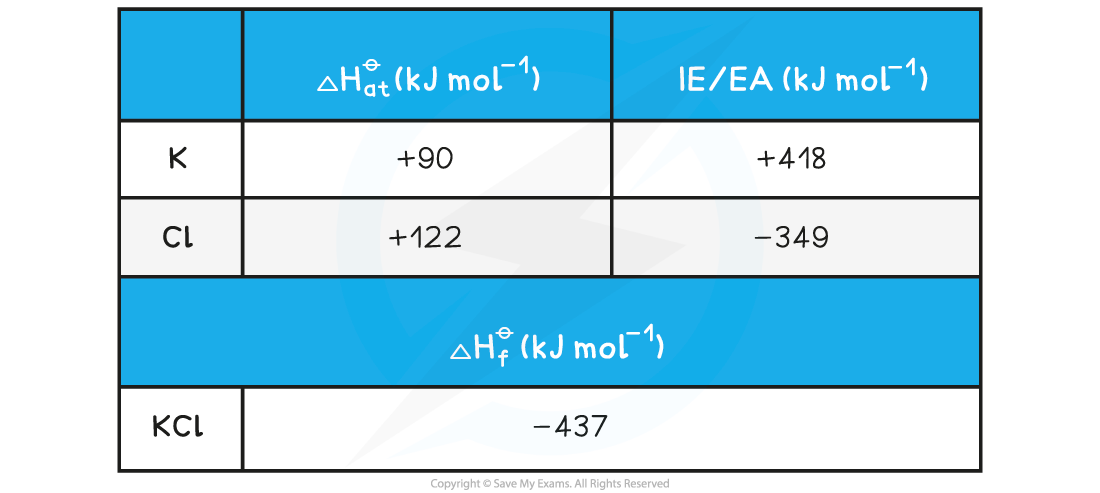
Answer

Step 1: Construct the Born-Haber cycle

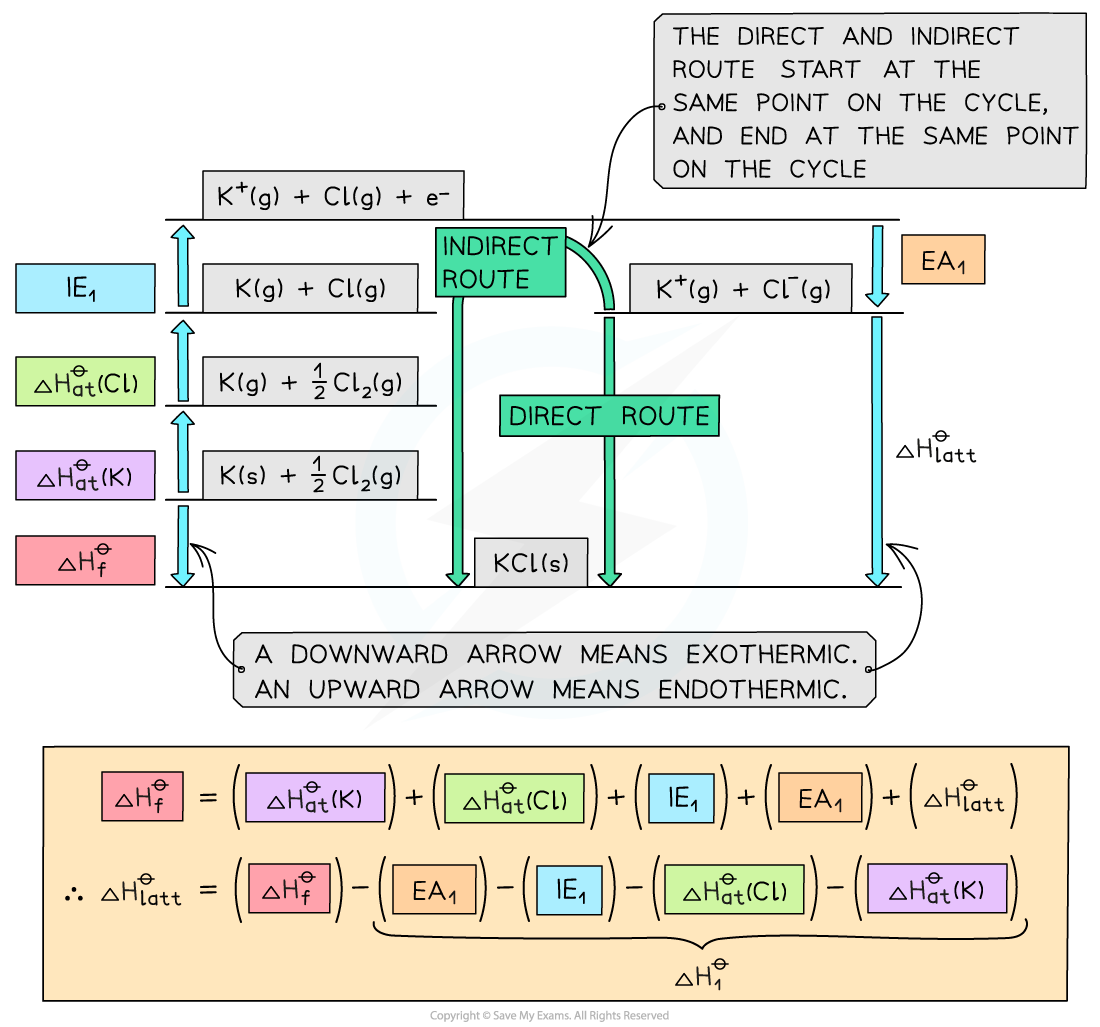
Step 2: Applying Hess’ law, the lattice energy of KCl is:

ΔH_lat^ꝋ = ΔH_f^ꝋ - ΔH₁^ꝋ

ΔH_latt^ꝋ = ΔH_f^ꝋ - [(ΔH_at^ꝋ K) + (ΔH_at^ꝋ Cl) + (IE₁ K) + (EA₁ Cl)]

Step 3: Substitute in the numbers:

ΔH_lat^ꝋ = (-437) - [(+90) + (+122) + (+418) + (-349)] = -718 kJ mol^-1

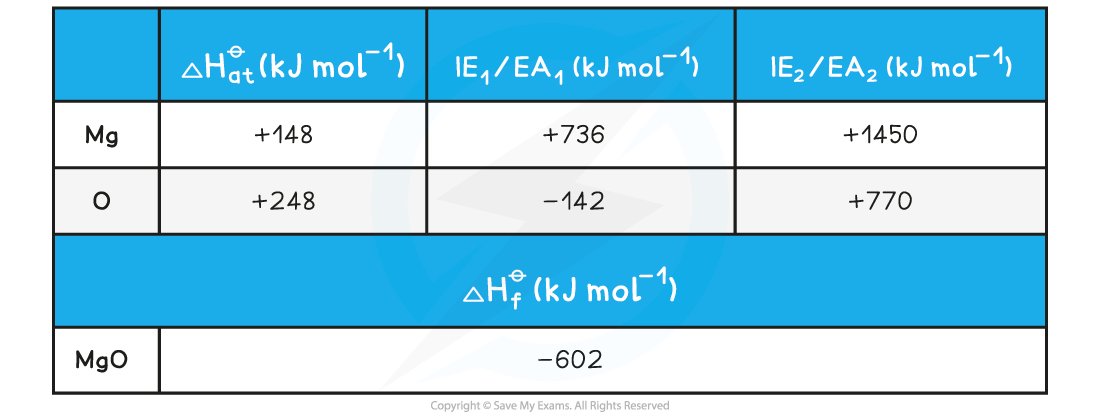
Answer

Step 1: Construct the Born-Haber cycle

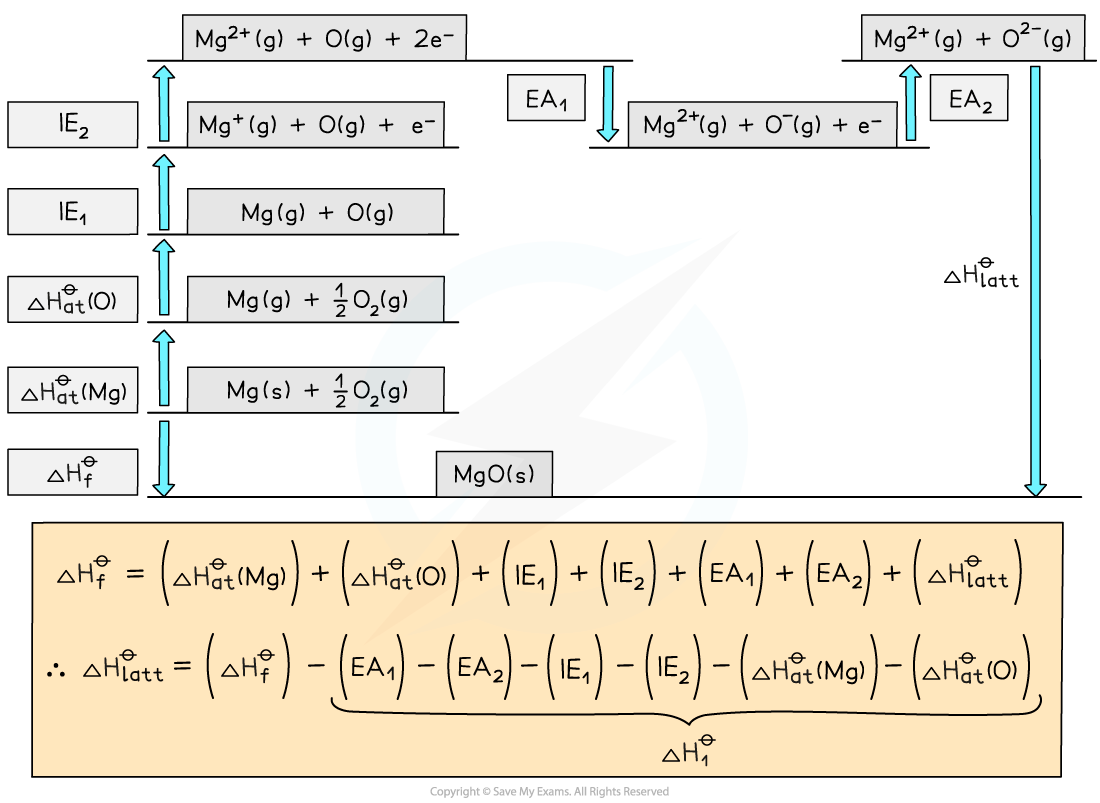
Step 2: Applying Hess’ law, the lattice energy of MgO is:

ΔH_latt^ꝋ = ΔH_f^ꝋ - ΔH₁^ꝋ

ΔH_lat^ꝋ = ΔH_f^ꝋ - [(ΔH_at^ꝋ Mg) + (ΔH_at^ꝋ O) + (IE₁ Mg) + (IE₂ Mg) + (EA₁ O) + (EA₂ O)]

Step 3: Substitute in the numbers:

ΔH_lat^ꝋ = (-602) - [(+148) + (+248) + (+736) + (+1450) + (-142) + (+770)]

= -3812 kJ mol^-1

Factors affecting lattice enthalpy

• The two key factors which affect lattice energy, ΔH_lat^ꝋ, are the ionic charge and ionic radii of the ions that make up the crystalline lattice

Ionic Radius

• The radius of the anion increases as you move down a group
• As the distance between the bonded ions increases, the strength of the electrostatic attraction decreases
• This is reflected by a decrease in the lattice enthalpy
• The lattice enthalpy becomes more negative or more exothermic as the ionic radius of the ions increases
• This is because the charge on the ions is more spread out over the ion when the ions are larger
• The ions are also further apart from each other in the lattice
  • The attraction between ions is between the centres of the ions involved, so the bigger the ions the bigger the distance between the centre of the ions
• Therefore, the electrostatic forces of attraction between the oppositely charged ions in the lattice are weaker
• For example, down group 17, the ionic radii increases which directly influences the lattice enthalpy

Lattice enthalpies of sodium halides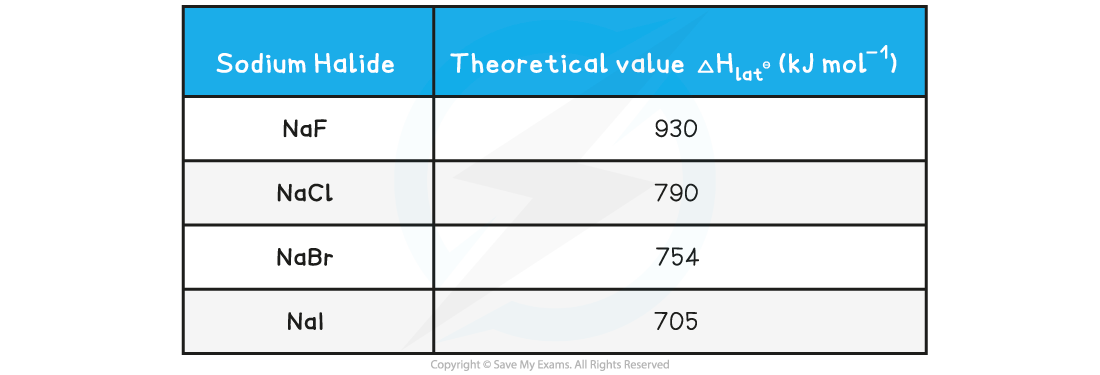

Ionic Charge

• Increasing the ionic charge will result in an increased attraction between oppositely charged ions
• This will increase the energy required to break the lattice apart, and therefore increase the lattice enthalpy (becomes more positive or more endothermic)
• The greater the ionic charge, the higher the charge density
• This results in stronger electrostatic attraction between the oppositely charged ions in the lattice
• As a result, the lattice enthalpy is more endothermic
  • For example, the lattice energy of calcium oxide (CaO) is more endothermic than the lattice energy of potassium chloride (KCl)

Lattice enthalpies with varying ionic charges and radii