- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
AQA A Level Maths: Pure复习笔记2.9.2 Stretches
Stretches
What are graph transformations?
- When you alter a function in certain ways, the effects on the graph of the function can be described by geometrical transformations
- With a stretch all the points on the graph are moved towards or away from either the x or the y axis by a constant scale factor

What do I need to know about graph stretches?
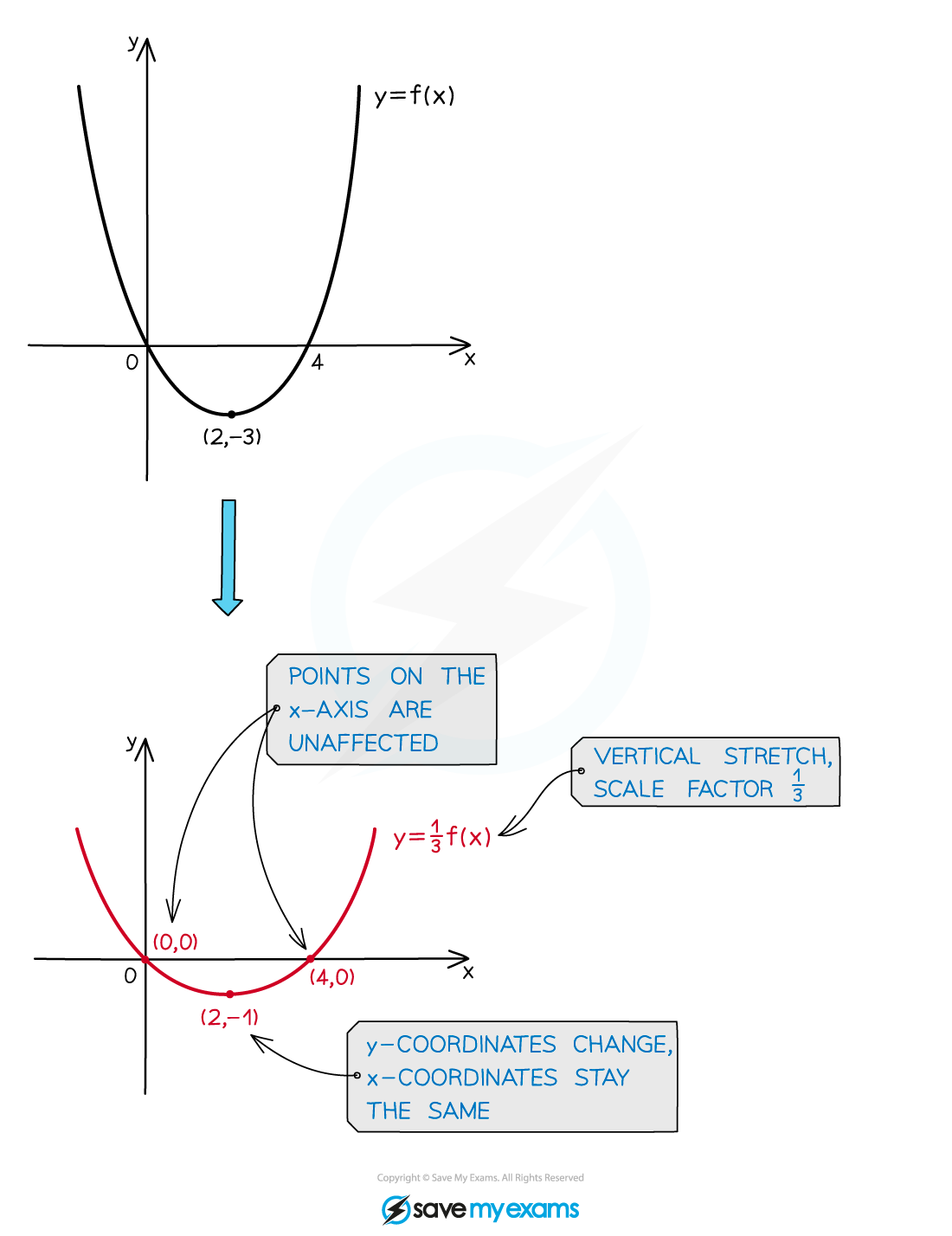
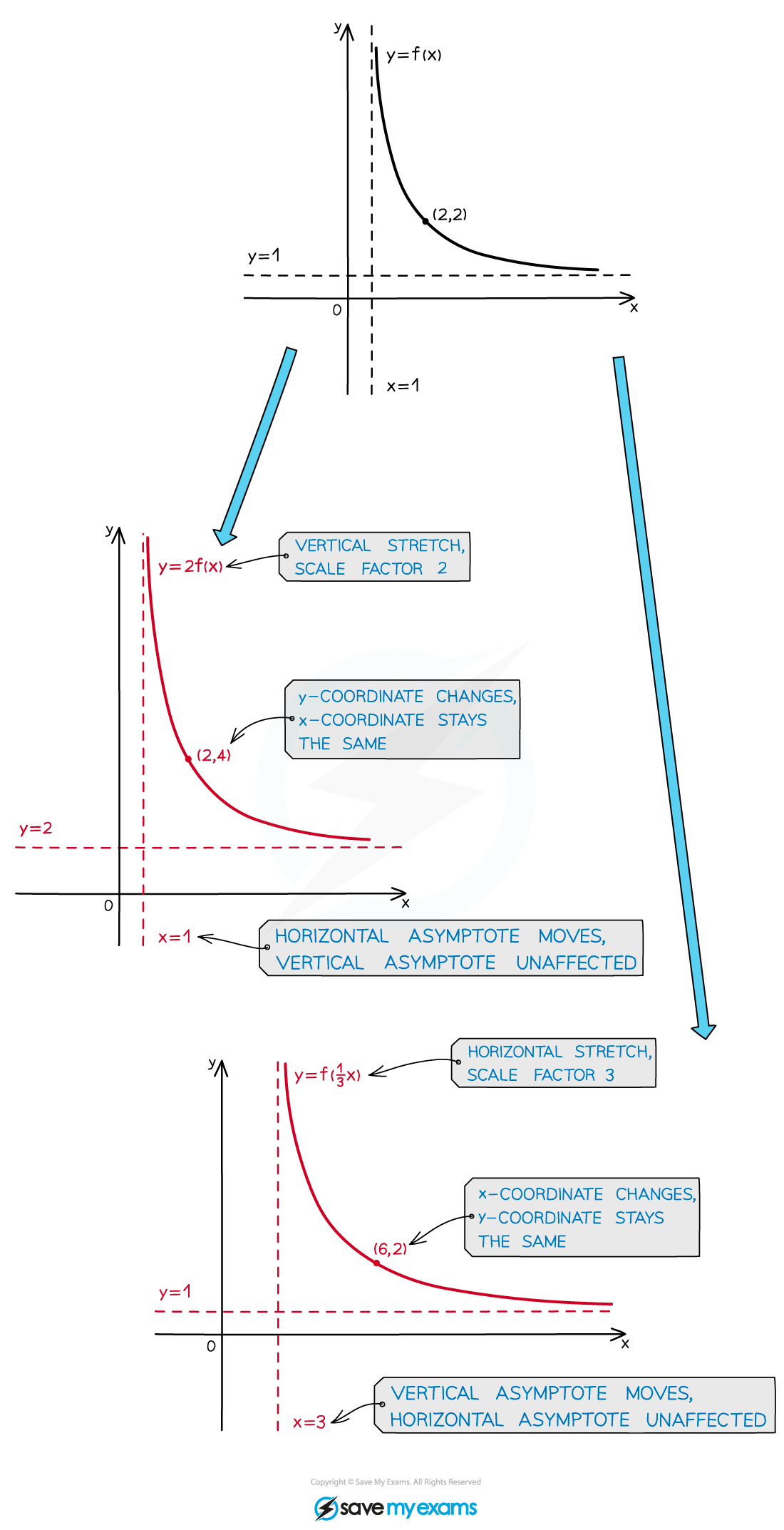
- The graph of y = af(x) is a vertical stretch of the graph y = f(x) by a scale factor of a, centred on the x axis
- The x coordinates of points stay the same; y coordinates are multiplied by a
- Points on the x axis stay where they are
- All other points move parallel to the y axis, away from (a > 1) or towards (0 < a < 1) the x axis
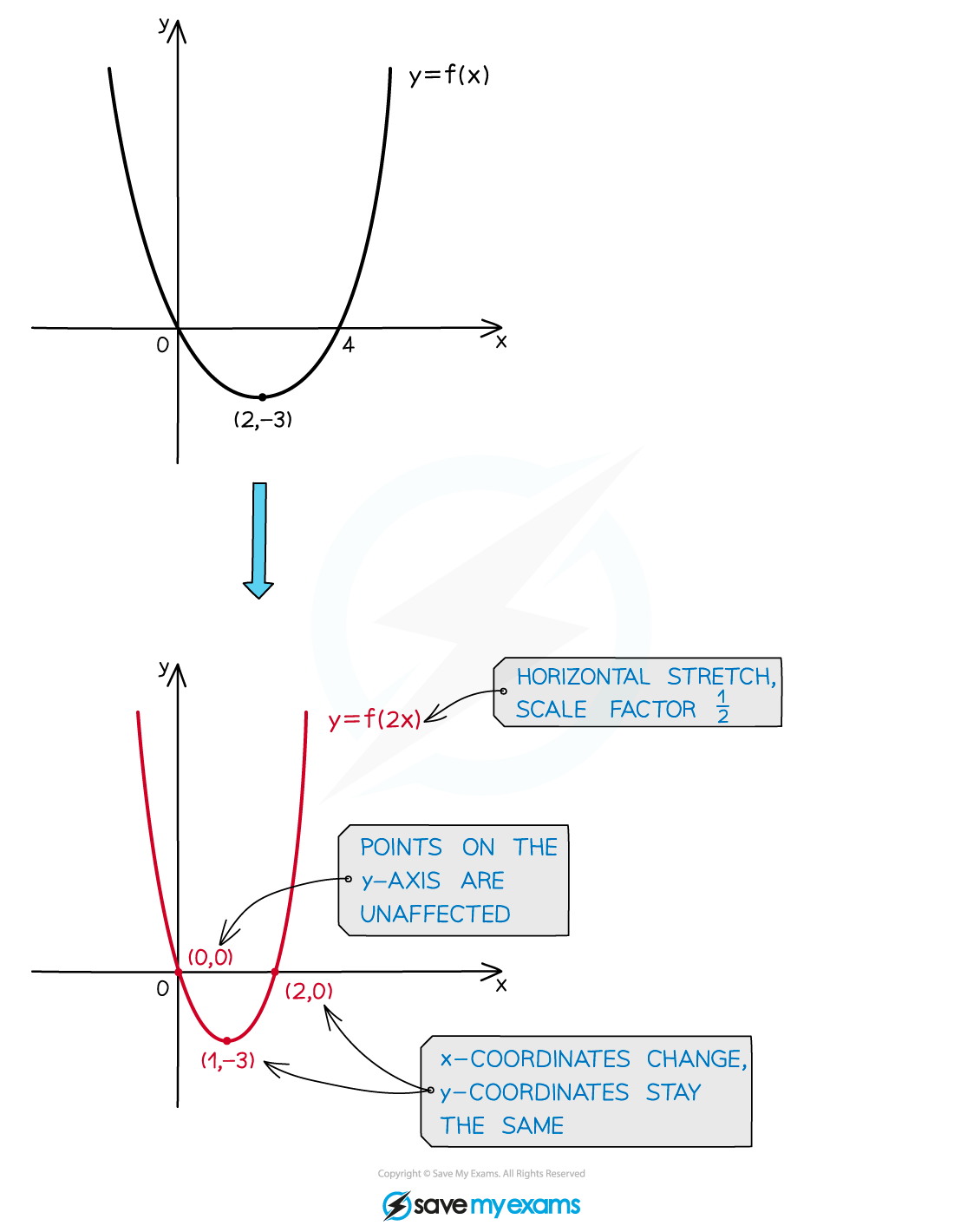
- The graph of y = f(ax) is a horizontal stretch of the graph y = f(x) by a scale factor of
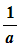 , centred on the y
, centred on the y
- The y coordinates of points stay the same; x coordinates are multiplied by
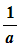
- Points on the y axis stay where they are
- All other points move parallel to the x axis, away from (0 < a < 1) or towards (a > 1) the y axis
- The y coordinates of points stay the same; x coordinates are multiplied by
- Any asymptotes of f(x) are also affected by the stretch (stretch them as you would stretch the function of a straight line)
- If an asymptote is one of the coordinate axes, or is parallel to the direction of the stretch, however, it will not be affected
Exam Tip
- When you sketch a stretched graph, be sure to indicate the new coordinates of any points that are marked on the original graph.
- Try to indicate the coordinates of points where the stretched graph intersects the coordinate axes (if you don't have the equation of the original function this may not be possible).
- If the graph has asymptotes, don't forget to sketch the asymptotes of the stretched graph as well.
Worked Example
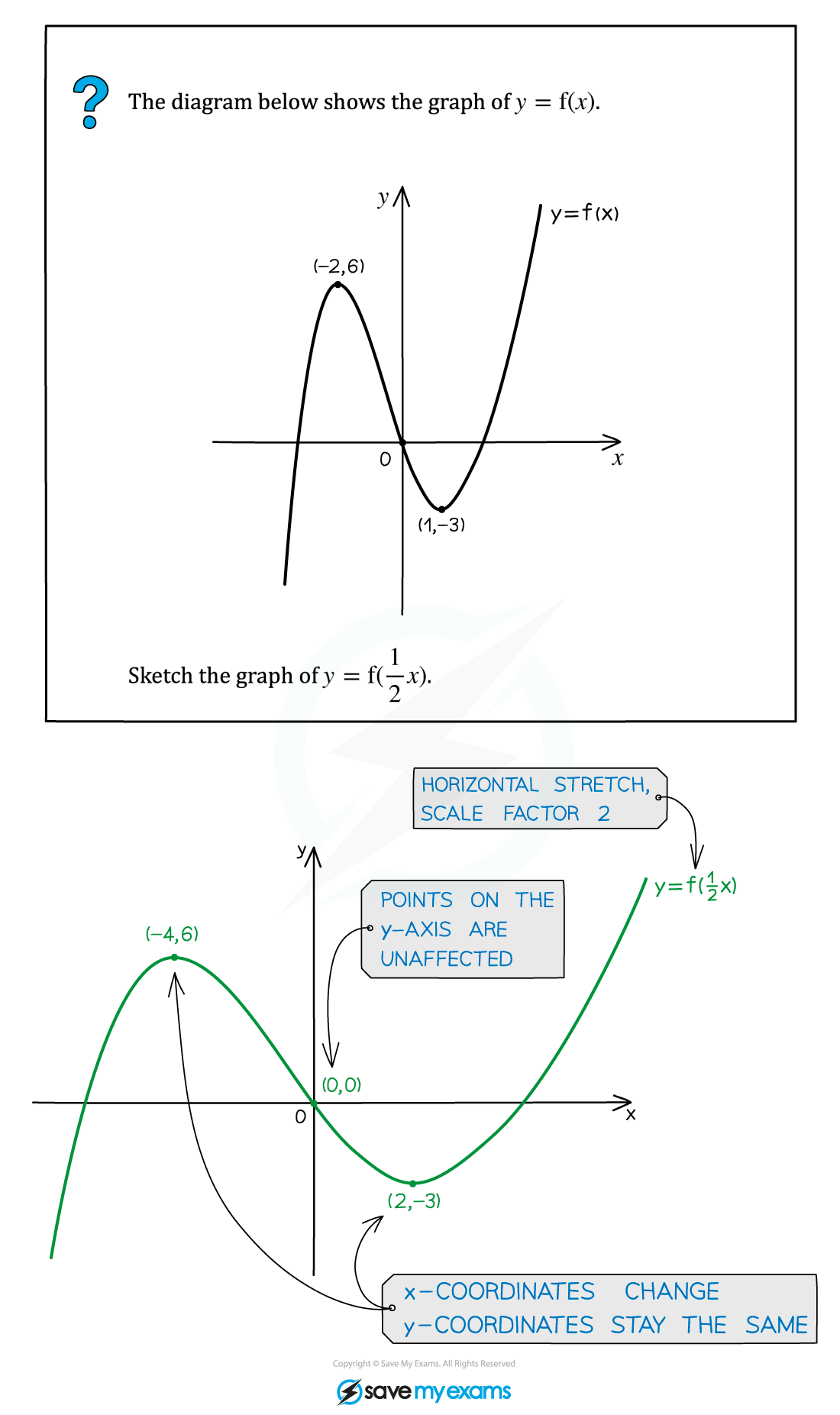
转载自savemyexams

在线登记
最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








