简单的三角函数及应用

涉及到A-Level或者Pre-Cal的数学，其中一个必学的内容就是三角函数(trigonometric function)。

今天，我们介绍一些简单的三角函数的定义及应用，以便于同学们记忆和理解。

首先我们需要认识并且记住直角三角形(rectangle)里的每条边的名称：

对边(opposite edge/side), 斜边(hypotenuse)，邻边(adjacent edge/side)

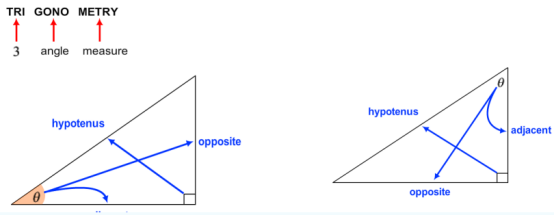
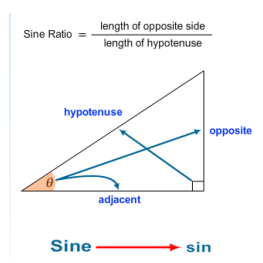
万事俱备，我们首先定义正弦函数sin：

在直角三角形中，

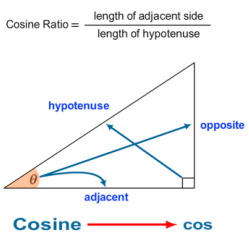
当然，还有我们经常用得到的余弦函数cos:

在直角三角形中，

 

当然，少不了的还有正切函数tan:

在直角三角形中，

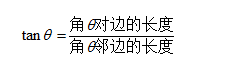
需要注意的是，之所以我们用到了比例(Ratio)一词，因为三角函数的值,只取决于角Θ的大小，而不取决于直角三角形面积的大小。

 

涉及到三角函数的应用

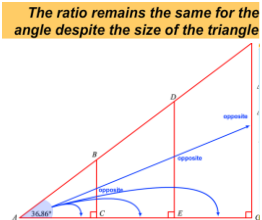
涉及到三角函数的一个简单的应用是，已知直角三角形内若干条边的长度，如何反推三角形的内角的大小。

例如下面一个例题：

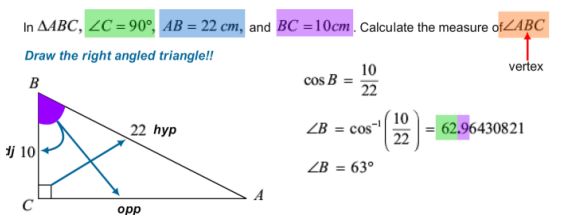
在直角三角形ABC中，角C是直角，斜边AB的长度是22cm,直角边BC的长度是10cm,求锐角B的大小。

分析：

在解决这个题的时候，很明显地，我们可以通过斜边AB和直角边BC两条边的长度关系，同时利用到我们刚介绍过的三个三角函数sin、cos、tan的定义,得出cosB的具体数值。最后，我们可以利用手中的计算器中的cos﹣¹这个功能，所得出的余弦数值为10/22的角度大小，即为我们想求得的锐角B的大小。

用数学文字表达出来的具体的解题过程，同学们可以参照下图：

张老师今天再给同学们分享一个关于三角函数的比较复杂的应用题。

同学们可以先试着自己独立解题。

如果在分析和解题过程中遇到困难，同学们可以依次参照下面三图，

图一、图二、图三分别按照分析和解题的逻辑顺序，详尽地解决了本题。

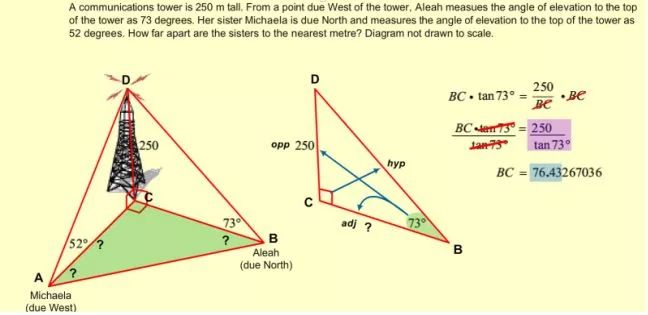
图一

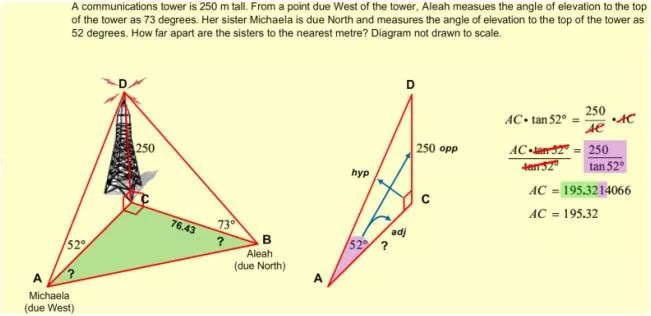
图二

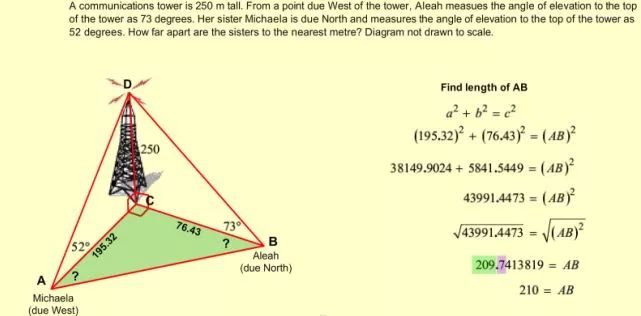
图三

其实，定义三角函数并非必须先定义单位圆(unit circle)。我们今天学习的方式，是仅仅借助直角三角形，就简洁地定义了正弦、余弦、正切三个三角函数。学好这三个基本的三角函数，并且相互之间不混淆，同学们就可以轻松地驾驭关于三角函数的更复杂的知识，做到触类旁通啦~