IB DP Maths: AI HL复习笔记5.7.1 Coupled Differential Equations
Solving Coupled Differential Equations
How do I write a system of coupled differential equations in matrix form?
How do I find the exact solution for a system of coupled differential equations?
Worked Example
Phase Portraits
What is a phase portrait for a system of coupled differential equations?
-
- These lines will define two sets of solution trajectories
- If the eigenvalue corresponding to a line’s eigenvector is positive, then there will be solution trajectories along the line away from the origin in both directions as t increases
- If the eigenvalue corresponding to a line’s eigenvector is negative, then there will be solution trajectories along the line towards the origin in both directions as t increases
- No solution trajectory will ever cross an eigenvector line
- If both eigenvalues are positive then all solution trajectories will be directed away from the origin as t increases
- In between the ‘eigenvector lines’ the trajectories as they move away from the origin will all curve to become approximately parallel to the line whose eigenvector corresponds to the larger eigenvalue
- If both eigenvalues are negative then all solution trajectories will be directed towards the origin as t increases
- In between the ‘eigenvector lines’ the trajectories will all curve so that at points further away from the origin they are approximately parallel to the line whose eigenvector corresponds to the more negative eigenvalue
- They will then converge on the other eigenvalue line as they move in towards the origin
- In between the ‘eigenvector lines’ the trajectories will all curve so that at points further away from the origin they are approximately parallel to the line whose eigenvector corresponds to the more negative eigenvalue
- If one eigenvalue is positive and one eigenvalue is negative then solution trajectories will generally start by heading in towards the origin before curving to head out away again from the origin as t increases
- In between the ‘eigenvector lines’ the solution trajectories will all move in towards the origin along the direction of the eigenvector line that corresponds to the negative eigenvalue, before curving away and converging on the eigenvector line that corresponds to the positive eigenvalue as they head away from the origin
-
The directions of the trajectories at those points tell us that the directions of the trajectories will be anticlockwise- They also tell us that the trajectories will be ellipses
- For circular trajectories, the direction of the trajectories when they cross a coordinate axis will be perpendicular to that coordinate axis
- For circular trajectories, the direction of the trajectories when they cross a coordinate axis will be perpendicular to that coordinate axis
-
- The directions of the trajectories at those points tell us that the directions of the trajectory spirals will be clockwise
Worked Example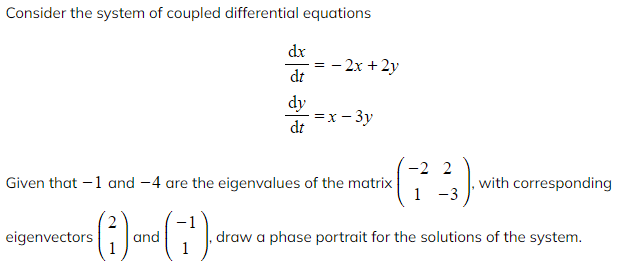
Equilibrium Points
What is an equilibrium point?
-
-
- All solution trajectories here spiral away from the origin
-
Worked Example
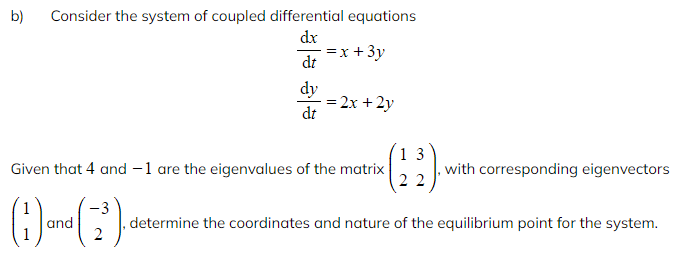
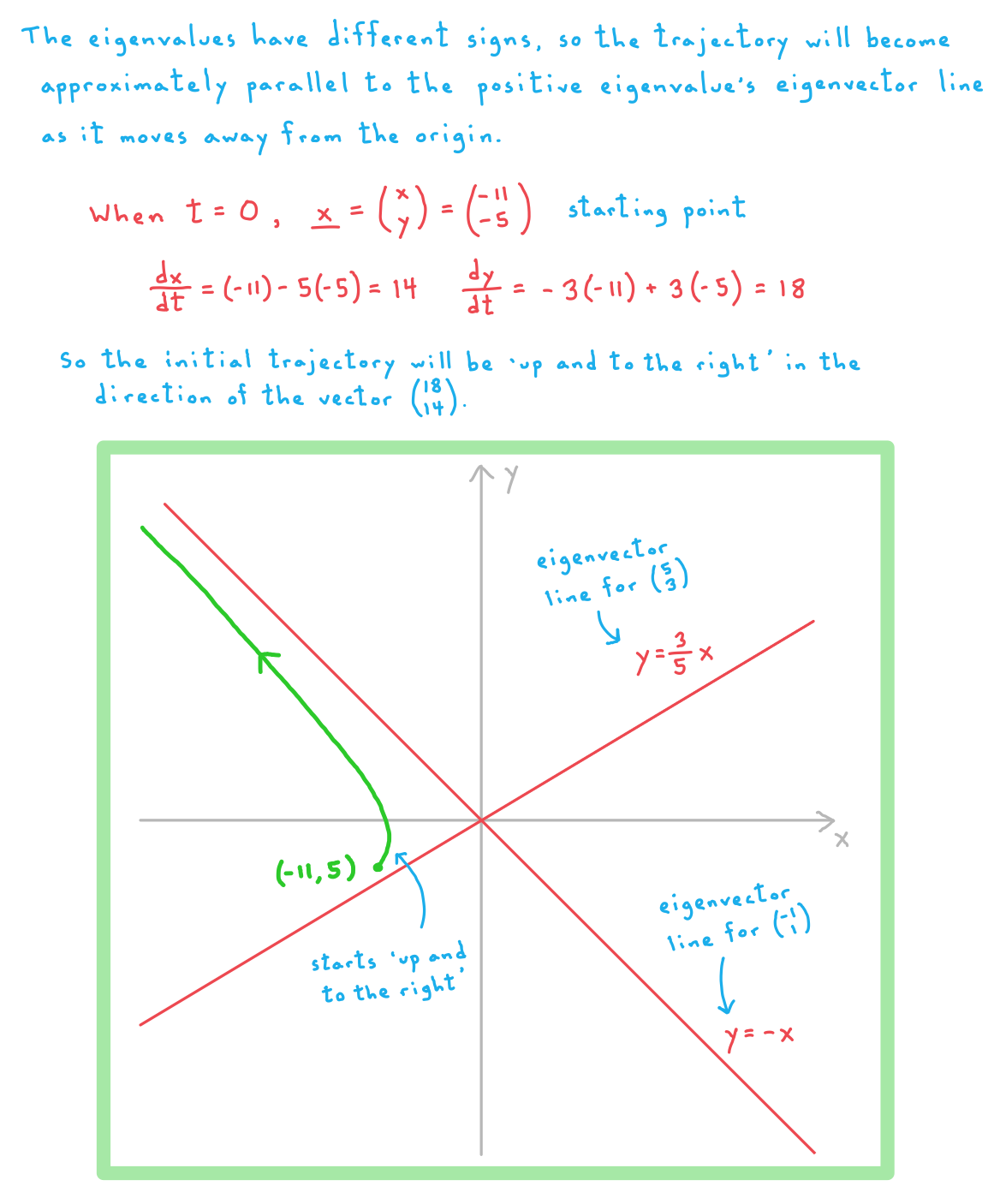
Sketching Solution Trajectories
How do I sketch a solution trajectory for a system of coupled differential equations?
- A phase portrait shows typical trajectories representing all the possible solutions to a system of coupled differential equations
- For a given set of initial conditions, however, the solution will only have one specific trajectory
- Sketching a particular solution trajectory will generally involve the following:
- Make sure you know what the ‘typical’ solutions for the system look like
- You don’t need to sketch a complete phase portrait unless asked, but you should know what the phase portrait for your system would look like
- If the phase portrait includes ‘eigenvector lines’, however, it is worth including these in your sketch to serve as guidelines
Use the above considerations to create your sketch
- The trajectory should begin at the starting point (be sure to mark and label the starting point on your sketch!)
- It should move away from the starting point in the correct initial direction
- As it moves further away from the starting point, the trajectory should conform to the nature of a ‘typical solution’ for the system
- Make sure you know what the ‘typical’ solutions for the system look like
Worked Example
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
AMC8备考管家服务全新上线！
