- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Maths: AI HL复习笔记5.6.3 Slope Fields
Slope Fields
What are slope fields?
-
 Normally the tangent lines will be drawn for points that form a regularly-spaced grid of x and y values
Normally the tangent lines will be drawn for points that form a regularly-spaced grid of x and y values
How can I use slope fields to study the solutions of a differential equation?
- Looking at the tangent lines in a slope field diagram will give you a general sense for what the solution curves to the differential equation will look like
- Remember that the solution to a given differential equation is actually a family of solutions
- We need appropriate boundary conditions or initial conditions to determine which of that family of solutions is the precise solution in a particular situation
- You can think of the tangent lines in a slope diagram as ‘flow lines’
- From a given point the solution curve through that point will ‘flow’ away from the point in the direction of the tangent line
- For a given point, you can use a slope field to sketch the general shape of the solution curve that goes through that point
- The given point here serves as a boundary condition, letting you know which of all the possible solution curves is the one you want to sketch
- The sketch should go through the given point, and follow the general ‘flow’ of the tangent lines through the rest of the slope field diagram
- In general, the sketched solution curve should not attempt to connect together a number of different tangent lines in the diagram
- There is no guarantee that the solution curve will go through any exact point in the ‘grid’ of points at which tangent lines have been drawn
- The only tangent line that your solution curve should definitely go through is one at the given ‘boundary condition’ point
- The sketched solution curve may go along some of the tangent lines, but it should not should not cut across any of them
- Look out for places where the tangent lines are horizontal
 Worked Example
Worked Example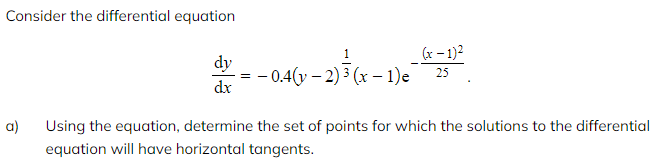




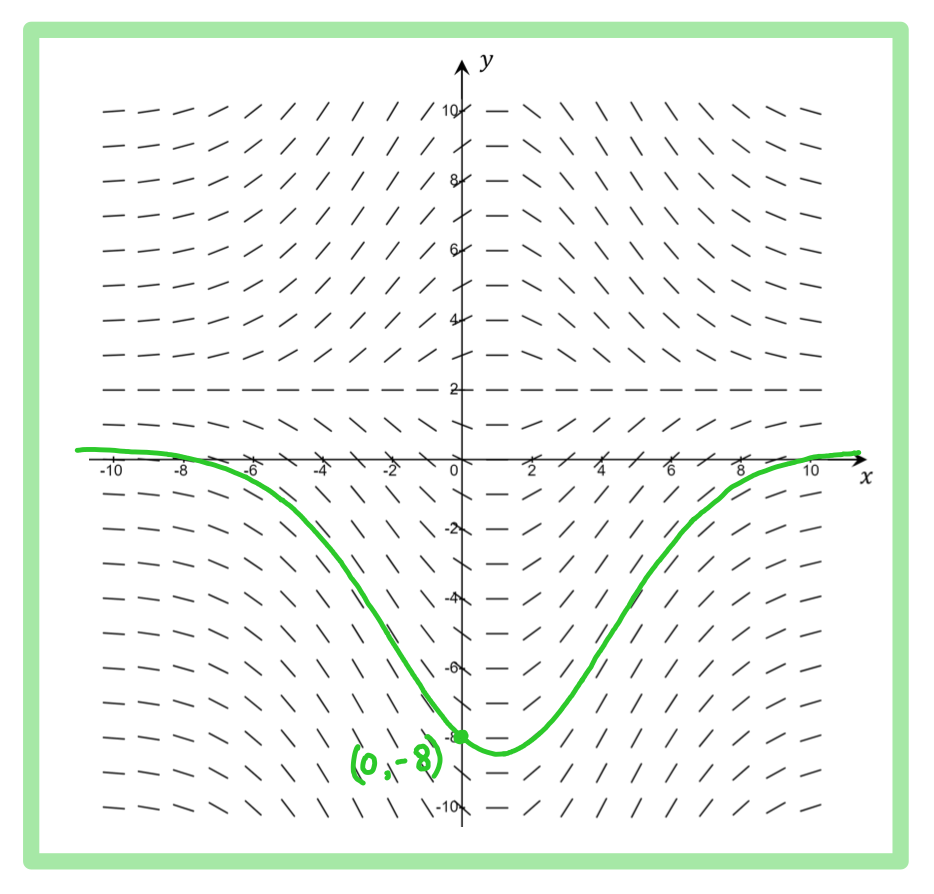
转载自savemyexams

最新发布
© 2026. All Rights Reserved. 沪ICP备2023009024号-1









