IB DP Maths: AI HL复习笔记5.1.3 Modelling with Differentiation
Modelling with Differentiation
What can be modelled with differentiation?
- Recall that differentiation is about the rate of change of a function and provides a way of finding minimum and maximum values of a function
- Anything that involves maximising or minimising a quantity can be modelled using differentiation; for example
- minimising the cost of raw materials in manufacturing a product
- the maximum height a football could reach when kicked
- These are called optimisation problems
What modelling assumptions are used in optimisation problems?
- The quantity being optimised needs to be dependent on a single variable
- If other variables are initially involved, constraints or assumptions about them will need to be made; for example
- minimising the cost of the main raw material – timber in manufacturing furniture say – the cost of screws, glue, varnish, etc can be fixed or considered negligible
- Other modelling assumptions may have to be made too; for example
- ignoring air resistance and wind when modelling the path of a kicked football
- If other variables are initially involved, constraints or assumptions about them will need to be made; for example
How do I solve optimisation problems?
Problems often start by linking two connected quantities together – for example volume and surface area
- where more than one variable is involved, constraints will be given such that the quantity of interest can be rewritten in terms of a single variable
- Once the quantity of interest is written as a function of a single variable, differentiation can be used to maximise or minimise the quantity as required
STEP 1
Rewrite the quantity to be optimised as a single variable, using any constraints given in the question
STEP 2
Use your GDC to find the (local) maximum or minimum points as required
Plot the graph of the function and use the graphing features of the GDC to “solve for minimum/maximum” as required
STEP 3
Note down the solution from your GDC and interpret the answer(s) in the context of the question
Exam Tip
- The first part of rewriting a quantity as a single variable is often a “show that” question – this means you may still be able to access later parts of the question even if you can’t do this bit
Worked Example
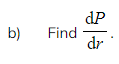
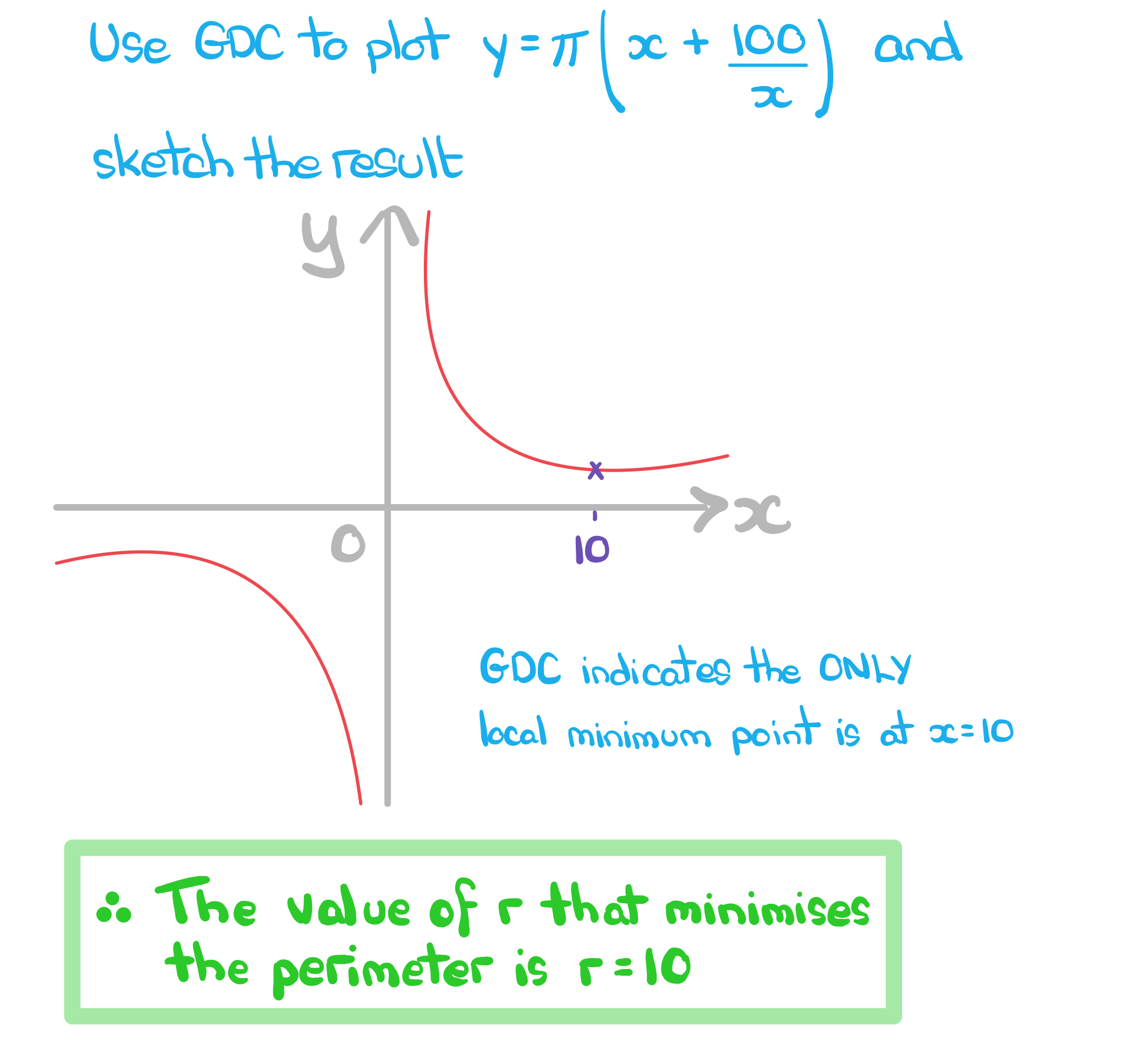
d)Hence find the minimum perimeter.
转载自savemyexams
国际竞赛真题资料-点击免费领取！
欧几里得竞赛 寒假集训班开课了！
USACO寒假集训来袭！点击咨询！
