- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Maths: AI HL复习笔记4.4.1 Probability & Types of Events
Probability Basics
What key words and terminology are used with probability?
- An experiment is a repeatable activity that has a result that can be observed or recorded
- Trials are what we call the repeats of the experiment
- An outcome is a possible result of a trial
- An event is an outcome or a collection of outcomes
- Events are usually denoted with capital letters: A, B, etc
- n(A) is the number of outcomes that are included in event A
- An event can have one or more than one outcome
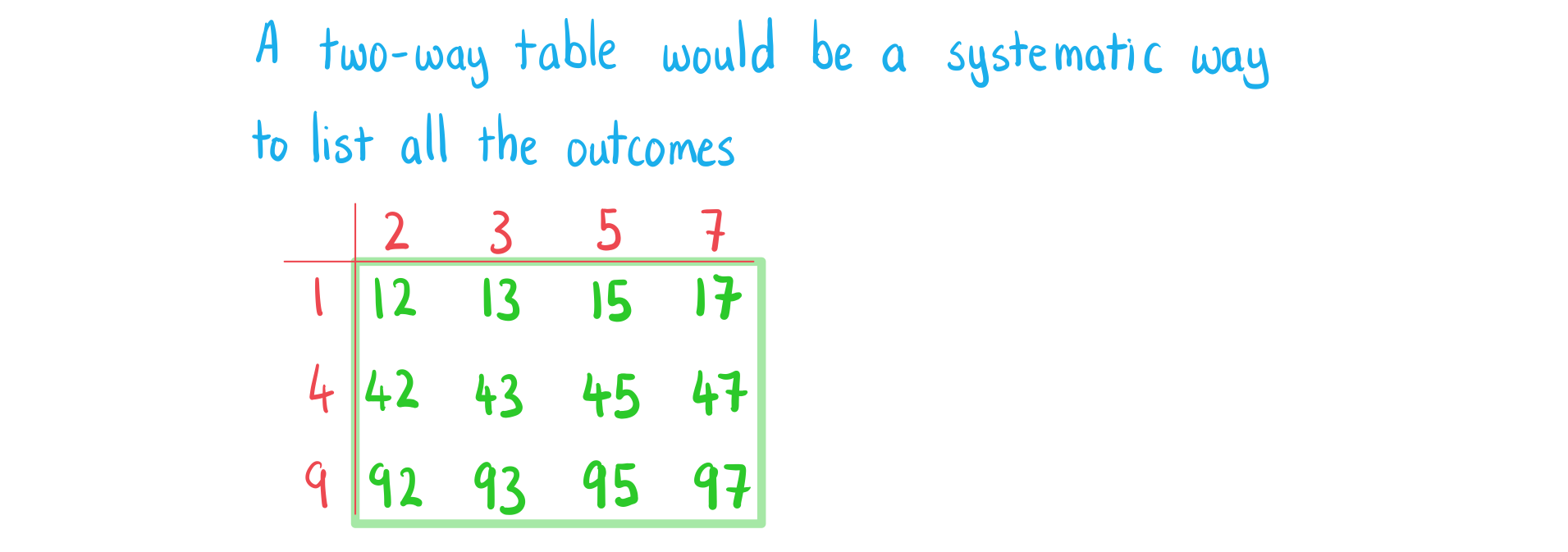
- A sample space is the set of all possible outcomes of an experiment
- This is denoted by U
- n(U) is the total number of outcomes
- It can be represented as a list or a table
How do I calculate basic probabilities?
- If all outcomes are equally likely then probability for each outcome is the same
 How do I calculate the expected number of occurrences of an outcome?
How do I calculate the expected number of occurrences of an outcome?
- Theoretical probability can be used to calculate the expected number of occurrences of an outcome from n trials
- If the probability of an outcome is p and there are n trials then:
- The expected number of occurrences is np
- This does not mean that there will exactly np occurrences
- If the experiment is repeated multiple times then we expect the number of occurrences to average out to be np
What is the complement of an event?
- The probabilities of all the outcomes add up to 1
- Complementary events are when there are two events and exactly one of them will occur
- One event has to occur but both events can not occur at the same time
- The complement of event A is the event where event A does not happen
- This can be thought of as not A
 What are different types of combined events?
What are different types of combined events?
 How do I find the probability of combined events?
How do I find the probability of combined events?
- The probability of A or B (or both) occurring can be found using the formula

- A rearranged version is given in the formula booklet
- Basically you multiply the probability of A by the probability of B then happening
Exam Tip
- In an exam drawing a Venn diagram or tree diagram can help even if the question does not ask you to
Worked Example
![]()
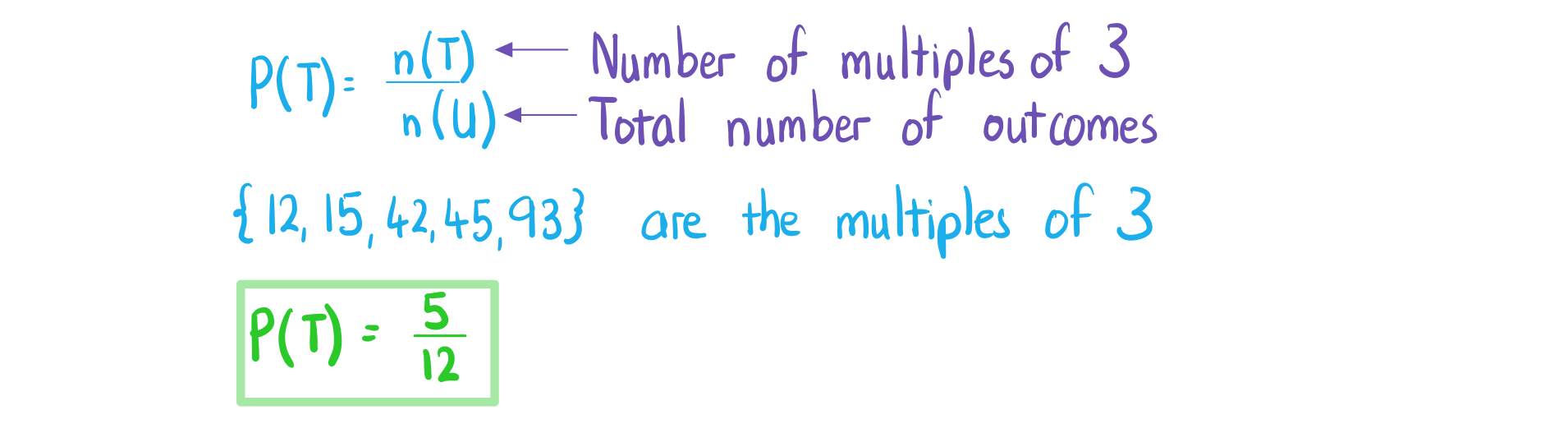
![]()
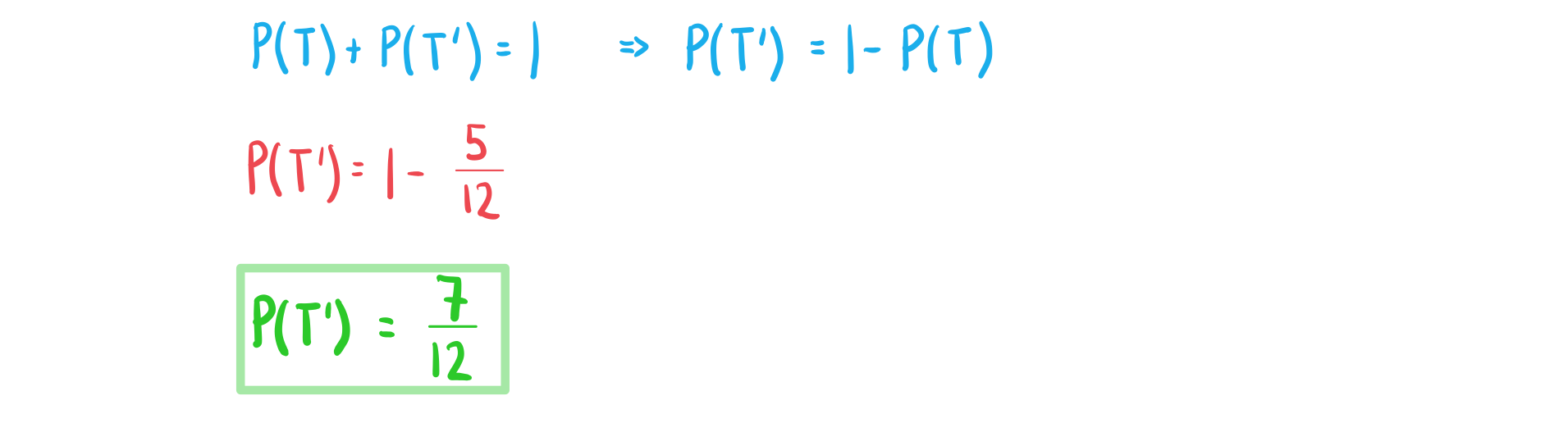
Independent & Mutually Exclusive Events
What are mutually exclusive events?
- Two events are mutually exclusive if they can not both happen at once
- For example: when rolling a dice the events “getting a prime number” and “getting a 6” are mutually exclusive
- If A and B are mutually exclusive events then:
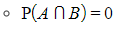 Complementary events are mutually exclusive
Complementary events are mutually exclusive
What are independent events?
- Two events are independent if one occurring does not affect the probability of the other occurring
- For example: when flipping a coin twice the events “getting a tails on the first flip” and “getting a tails on the second flip” are independent
- If A and B are independent events then:
-
-
 This is given in the formula booklet
This is given in the formula booklet- This is a useful formula to test whether two events are statistically independent
-
How do I find the probability of combined mutually exclusive events?
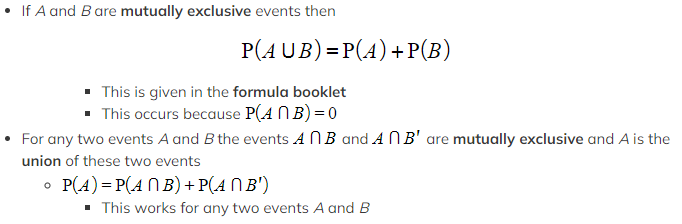 Worked Example
Worked Example
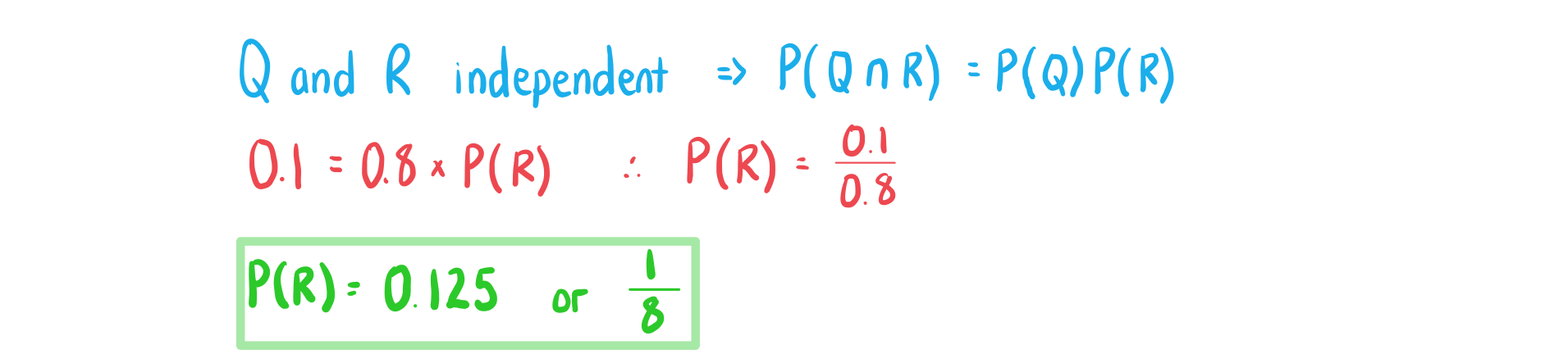
a)A student is chosen at random from a class. The probability that they have a dog is 0.8, the probability they have a cat is 0.6 and the probability that they have a cat or a dog is 0.9.
Find the probability that the student has both a dog and a cat.
Find the probability that the student has both a dog and a cat.




转载自savemyexams

在线登记
最新发布
翰林课程体验,退费流程快速投诉邮箱: yuxi@linstitute.net 沪ICP备2023009024号-1








