- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Maths: AI HL复习笔记3.10.3 Minimum Spanning Trees
Kruskal's Algorithm
In a situation that can be modelled by a graph, Kruskal’s algorithm is a mathematical tool that can be used to reduce costs, materials or time.
Why do we use Kruskal’s Algorithm?
- Kruskal’s algorithm is a series of steps that when followed will produce the minimum spanning tree for a connected graph
- Finding the minimum spanning tree is useful in a lot of practical applications to connect all of the vertices in the most efficient way possible
- The number of edges in a minimum spanning tree will always be one less than the number of vertices in the graph
- A cycle is a walk that starts at a given vertex and ends at the same vertex.
- A minimum spanning tree cannot contain any cycles.
What is Kruskal’s Algorithm?
- STEP 1
Sort the edges in terms of increasing weight - STEP 2
Select the edge of least weight (if there is more than one edge of the same weight, either may be used) - STEP 3
Select the next edge of least weight that has not already been chosen and add it to your tree provided that it does not make a cycle with any of the previously selected edges - STEP 4
Repeat STEP 3 until all of the vertices in the graph are connected
Exam Tip
- When using any of the algorithms for finding the minimum spanning tree, make sure that you state the order in which the edges are selected to get full marks for working!
Worked Example
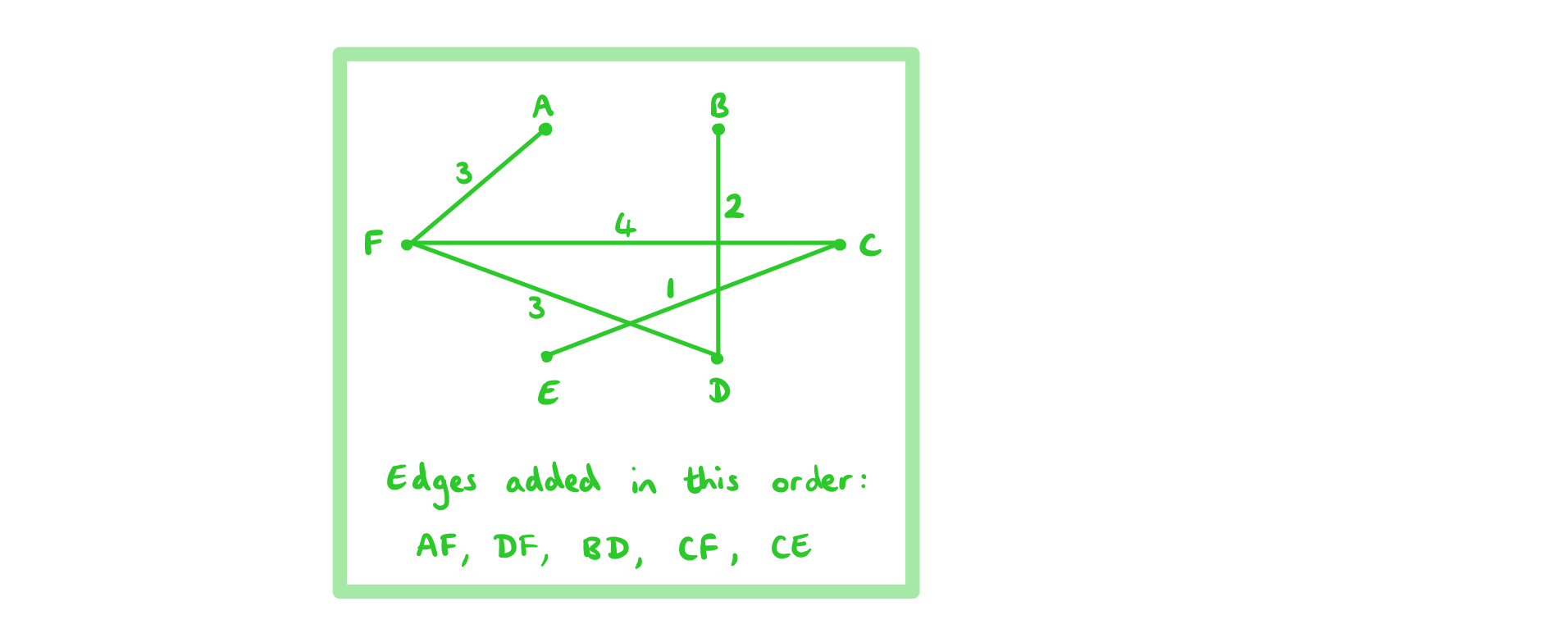
Consider the weighted graph G below.
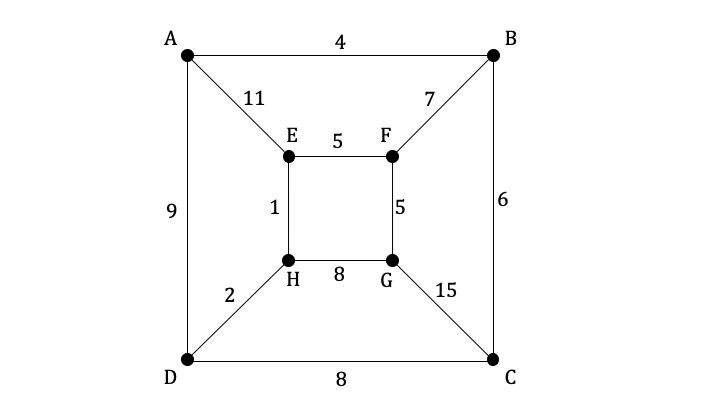
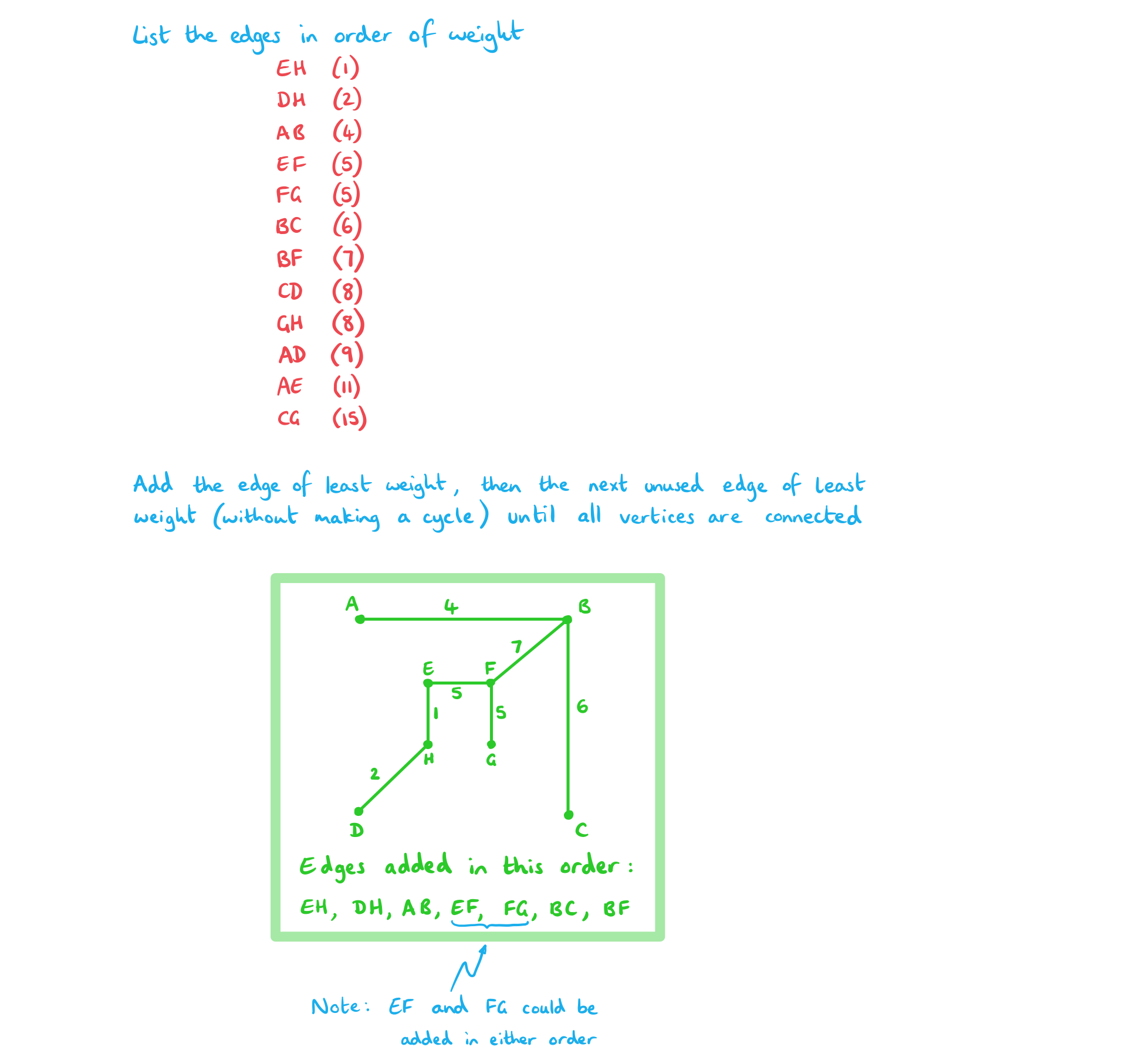

Prim's Algorithm
Prim’s algorithm is a second method of finding the minimum spanning tree of a graph.
What is Prim’s Algorithm?
- Prim’s algorithm involves adding edges from vertices that are already connected to the tree.
- Cycles are avoided by only adding edges that are not already connected at one end.
- STEP 1
Start at any vertex and choose the edge of least weight that is connected to it - STEP 2
Choose the edge of least weight that is incident (connected) to any of the vertices already connected and does not connect to another vertex that is already in the tree - STEP 3
Repeat STEP 2 until all of the vertices are added to the tree
Worked Example
Consider the weighted graph below.
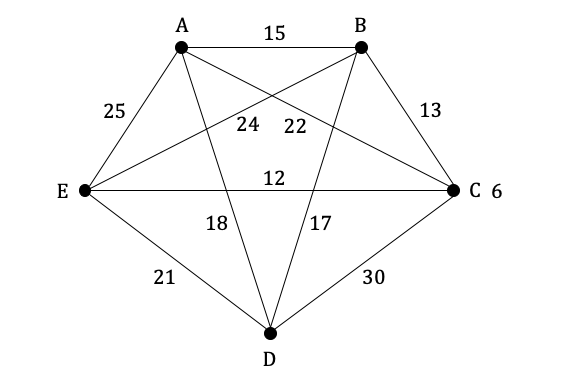


Prim's Algorithm Using a Matrix
Information may be given to you either in the form of a graph or as a weighted adjacency table. Prim’s algorithm can be adapted to be used from the adjacency matrix.
How do you apply Prim’s algorithm to a matrix?
- A minimum spanning tree is built up from the least weight edges that are incident to vertices already in the tree by looking at the relevant rows in the adjacency table
- STEP 1
Select any vertex to start from, cross out the values in the column associated with that vertex and label the row associated with the vertex 1 - STEP 2
Circle the lowest value in any cell along that row and add the edge to your tree, cross out the remaining values in the column of the cell that you have circled - STEP 3
Label the row associated with the same vertex as the column in the previous STEP with the next - STEP 4
Circle the lowest value in any cell along any of the rows that have been labelled and add the edge to your tree, cross out the remaining values in the column of the cell that you have circled - STEP 5
Repeat STEPS 3 and 4 until all rows have been labelled and all vertices have been added to the tree
Which should I use Prim’s or Kruskal’s Algorithm?
- Kruskal’s algorithm can be used when the information is in graph form whereas Prim’s algorithm can be used in either graph or matrix form.
- Prim’s algorithm is sometimes considered to be more efficient that Kruskal’s algorithm as
- the edges do not need to be ordered at the start and
- it does not rely on checking for cycles at each step
- An exam question will usually specify which method should be used, otherwise you have the choice
- If you are asked to find the minimum spanning tree and the information given in the question is in the form of a table, you should use Prim’s algorithm
Exam Tip
- Look out for questions that ask you to minimise the cost or length etc. from a weighted graph – they are implying that they want you to find the minimum spanning tree!
Worked Example
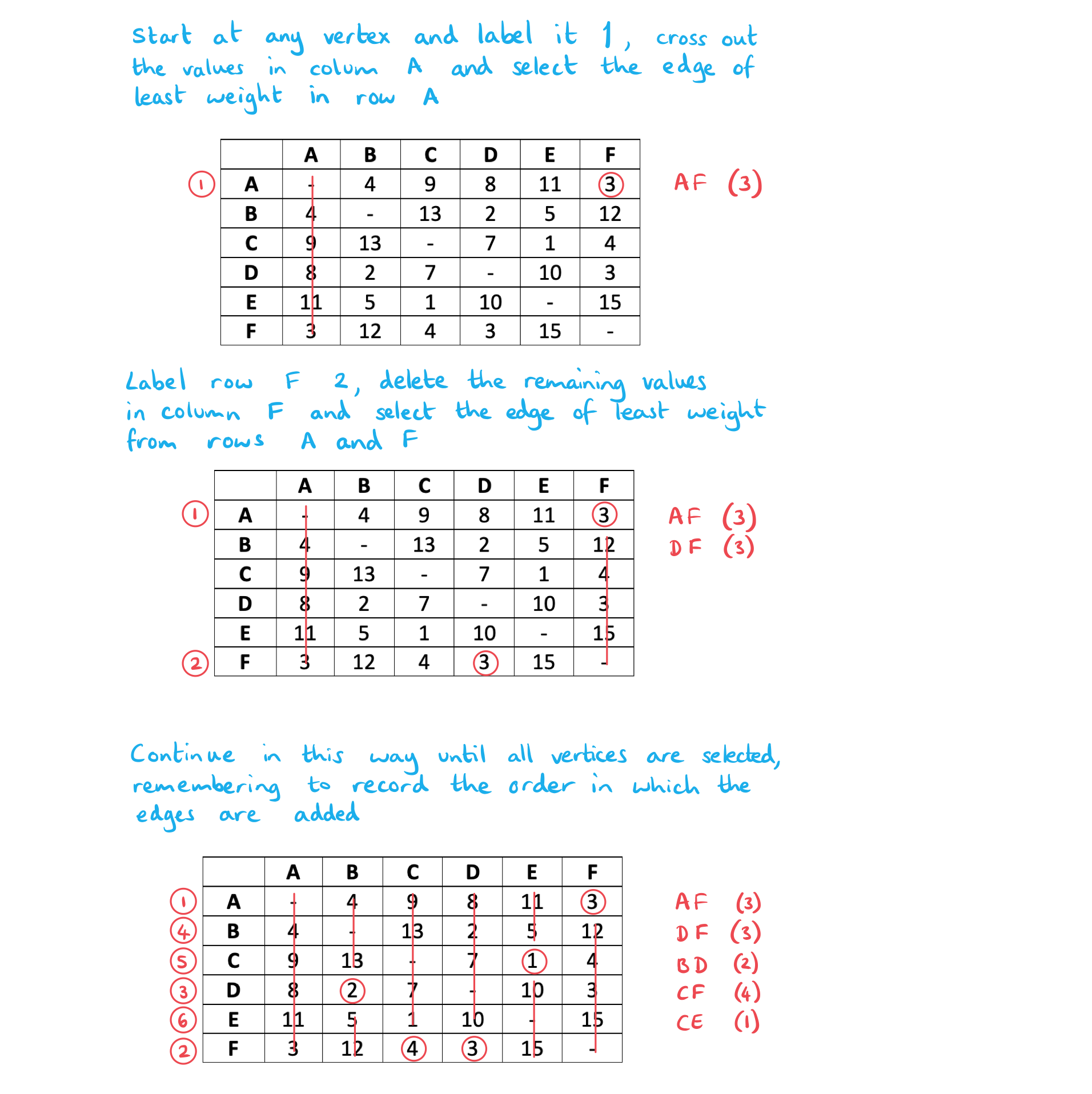
Celeste is building a model city incorporating 6 main buildings that need to be connected to an electrical supply.
Each vertex listed in the table below represents a building and the weighting of each edge is the cost in USD of creating a link to the electrical supply between the given vertices.
| A | B | C | D | E | F | |
| A | - | 4 | 9 | 8 | 11 | 3 |
| B | 4 | - | 13 | 2 | 5 | 12 |
| C | 9 | 13 | - | 7 | 1 | 4 |
| D | 8 | 2 | 7 | - | 10 | 3 |
| E | 11 | 5 | 1 | 10 | - | 15 |
| F | 3 | 12 | 4 | 3 | 15 | - |
Celeste wants to find the lowest cost solution that links all 6 buildings up to the electrical supply.

转载自savemyexams


最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








