- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Maths: AI HL复习笔记3.7.6 Components of Vectors
Components of Vectors
Why do we write vectors in component form?
- When working with vectors in context it is often useful to break them down into components acting in a direction that is not one of the base vectors
- The base vectors are vectors acting in the directions i, j and k
- The vector will need to be resolved into components that are acting perpendicular to each other
- Usually, one component will be acting parallel to the direction of another vector and the other will act perpendicular to the direction of the vector
- For example: the components of a force parallel and perpendicular to the line of motion allows different types of problems to be solved
- The parallel component of a force acting directly on a particle will be the component that causes an effect on the particle
- The perpendicular component of a force acting directly on a particle will be the component that has no effect on the particle
- The two components of the force will have the same combined effect as the original vector
How do we write vectors in component form?
- Use trigonometry to resolve a vector acting at an angle
- Given a vector a acting at an angle θ to another vector b
- Draw a vector triangle by decomposing the vector a into its components parallel and perpendicular to the direction of the vector b
- The vector a will be the hypotenuse of the triangle and the two components will make up the opposite and adjacent sides
- The component of a acting parallel to b will be equal to the product of the magnitude of a and the cosine of the angle θ
- The component of a acting in the direction of b equals |a|cos θ
 The formulae for the components using the scalar product and the vector product are particularly useful as the angle is not needed
The formulae for the components using the scalar product and the vector product are particularly useful as the angle is not needed
- The component of a acting in the direction of b equals |a|cos θ
- The question may give you the angle the vector is acting in as a bearing
- Bearings are always the angle taken from the north
Exam Tip
- If a question asks you to find a component of a vector it is a good idea to sketch a quick diagram so that you can visualise which vectors are going in which direction
- This is especially important if the question involves forces
Worked Example
A force with magnitude 10 N is acting on a bearing of 060° on an object which is moving with velocity vector v = 2i - 3j.
a)By finding the components of the force in the i and j direction, write down the force as a vector.
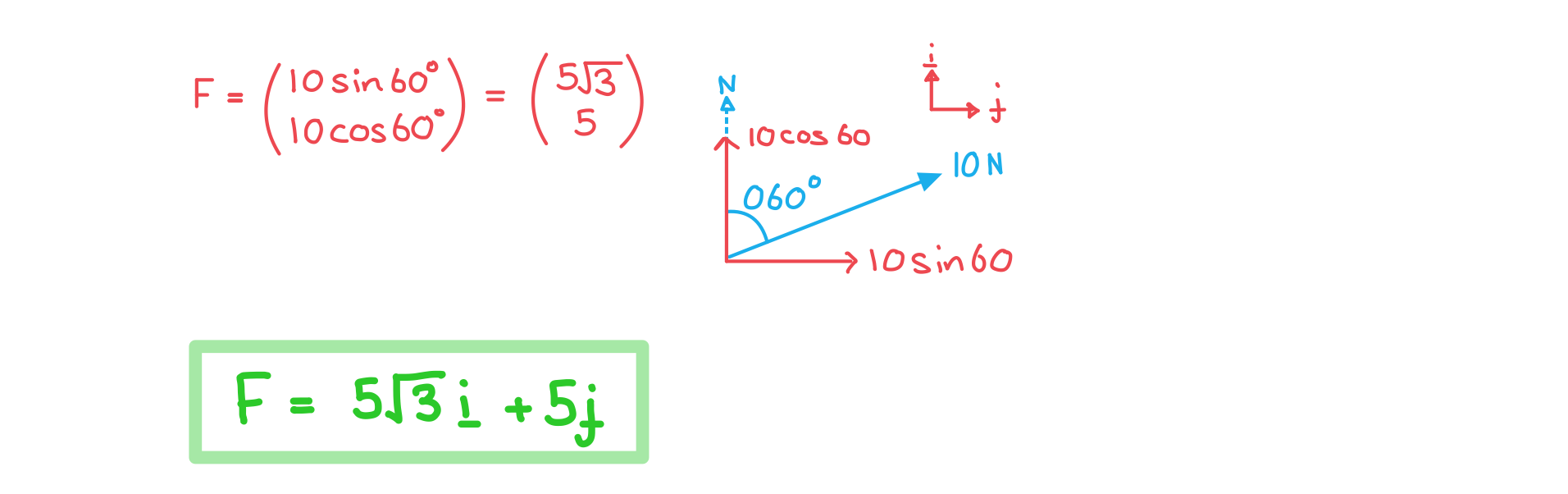
b)Find the component of the force acting parallel to the direction of the object.

转载自savemyexams

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








