- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Maths: AI HL复习笔记3.7.4 The Scalar Product
The Scalar ('Dot') Product
What is the scalar product?
- The scalar product (also known as the dot product) is one form in which two vectors can be combined together
 The result of taking the scalar product of two vectors is a real number
The result of taking the scalar product of two vectors is a real number
- i.e. a scalar
- The scalar product of two vectors gives information about the angle between the two vectors
- If the scalar product is positive then the angle between the two vectors is acute (less than 90°)
- If the scalar product is negative then the angle between the two vectors is obtuse (between 90° and 180°)
- If the scalar product is zero then the angle between the two vectors is 90° (the two vectors are perpendicular)
How is the scalar product calculated?
- There are two methods for calculating the scalar product
 The scalar product can be used in the second formula to find the angle between the two vectors
The scalar product can be used in the second formula to find the angle between the two vectors
What properties of the scalar product do I need to know?
 Exam Tip
Exam Tip
- Whilst the formulae for the scalar product are given in the formula booklet, the properties of the scalar product are not, however they are important and it is likely that you will need to recall them in your exam so be sure to commit them to memory
Worked Example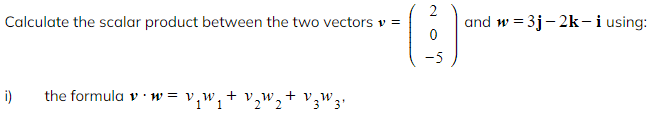

![]()

Angle Between Two Vectors
How do I find the angle between two vectors?
- If two vectors with different directions are placed at the same starting position, they will form an angle between them
- The two formulae for the scalar product can be used together to find this angle
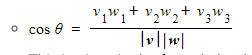 This is given in the formula booklet
This is given in the formula booklet
- To find the angle between two vectors:
- Calculate the scalar product between them
- Calculate the magnitude of each vector
- Use the formula to find cos θ
- Use inverse trig to find θ
Exam Tip
- The formula for this is given in the formula booklet so you do not need to remember it but make sure that you can find it quickly and easily in your exam
Worked Example

Perpendicular Vectors
How do I know if two vectors are perpendicular? Worked Example
Worked Example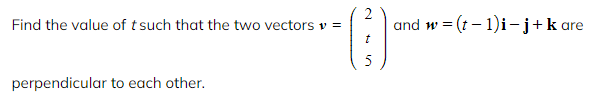

转载自savemyexams

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








