- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Maths: AI HL复习笔记3.3.2 Non Right-Angled Trigonometry
Sine Rule
What is the sine rule?
- The sine rule allows us to find missing side lengths or angles in non-right-angled triangles
- It states that for any triangle with angles A, B and C
-
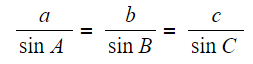 Where
Where
- a is the side opposite angle A
- b is the side opposite angle B
- c is the side opposite angle C
- This formula is in the formula booklet, you do not need to remember it
- Sin 90° = 1 so if one of the angles is 90° this becomes SOH from SOHCAHTOA
How can we use the sine rule to find missing side lengths or angles?
- The sine rule can be used when you have any opposite pairs of sides and angles
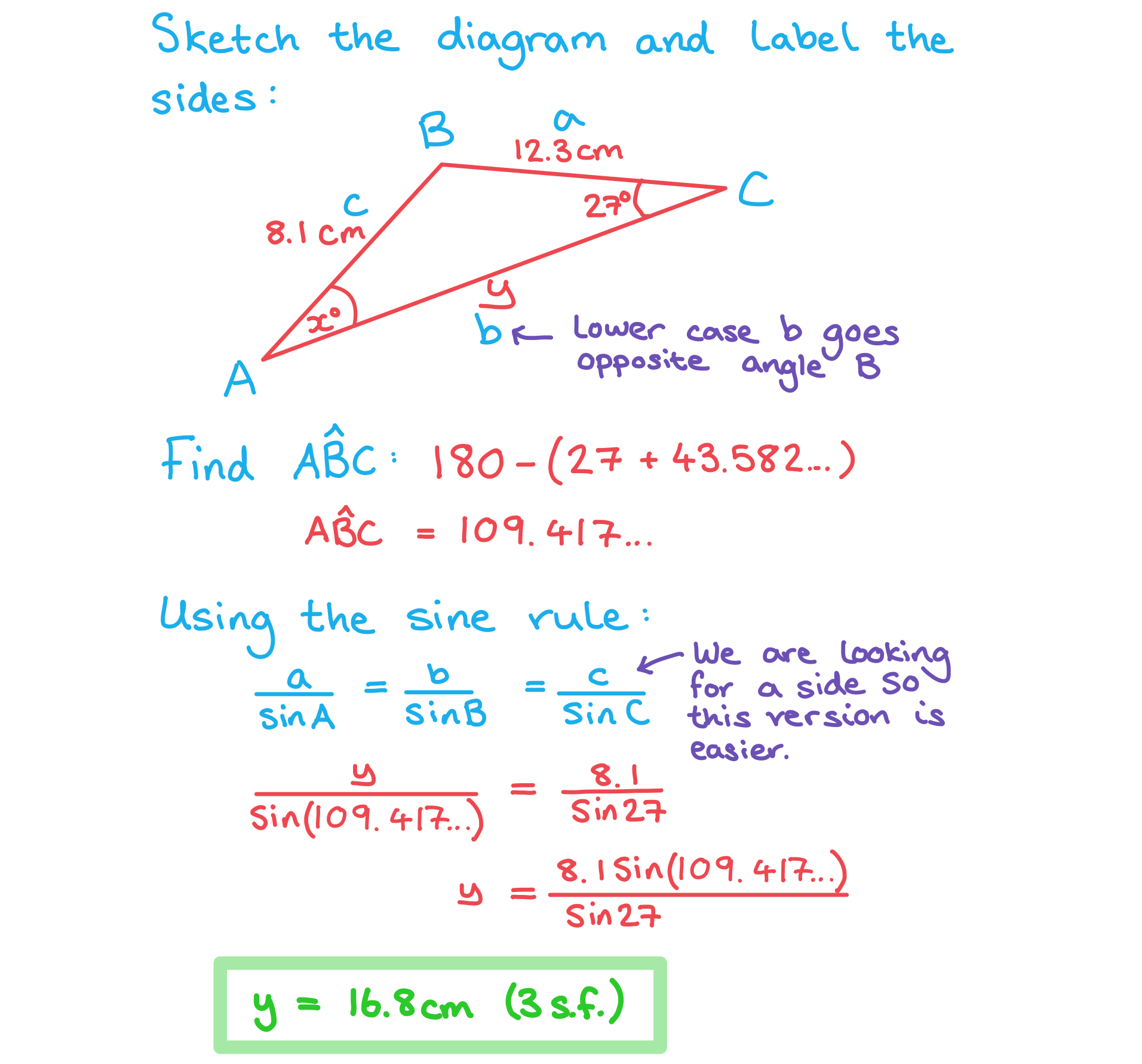
- Always start by labelling your triangle with the angles and sides
- Remember the sides with the lower-case letters are opposite the angles with the equivalent upper-case letters
- Use the formula in the formula booklet to find the length of a side
- To find a missing angle you can rearrange the formula and use the form
-
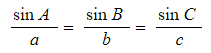 This is not in the formula booklet but can easily be found by rearranging the one given
This is not in the formula booklet but can easily be found by rearranging the one given
- Substitute the values you have into the formula and solve
Exam Tip
- If you're using a calculator make sure that it is in the correct mode (degrees/radians)
- Remember to give your answers as exact values if you are asked too
Worked Example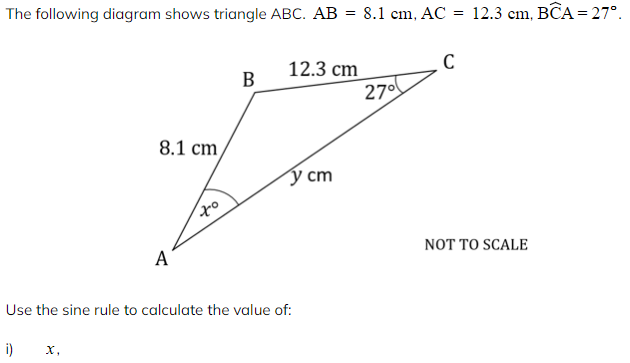

![]()
Ambiguous Sine Rule
What is the ambiguous case of the sine rule?
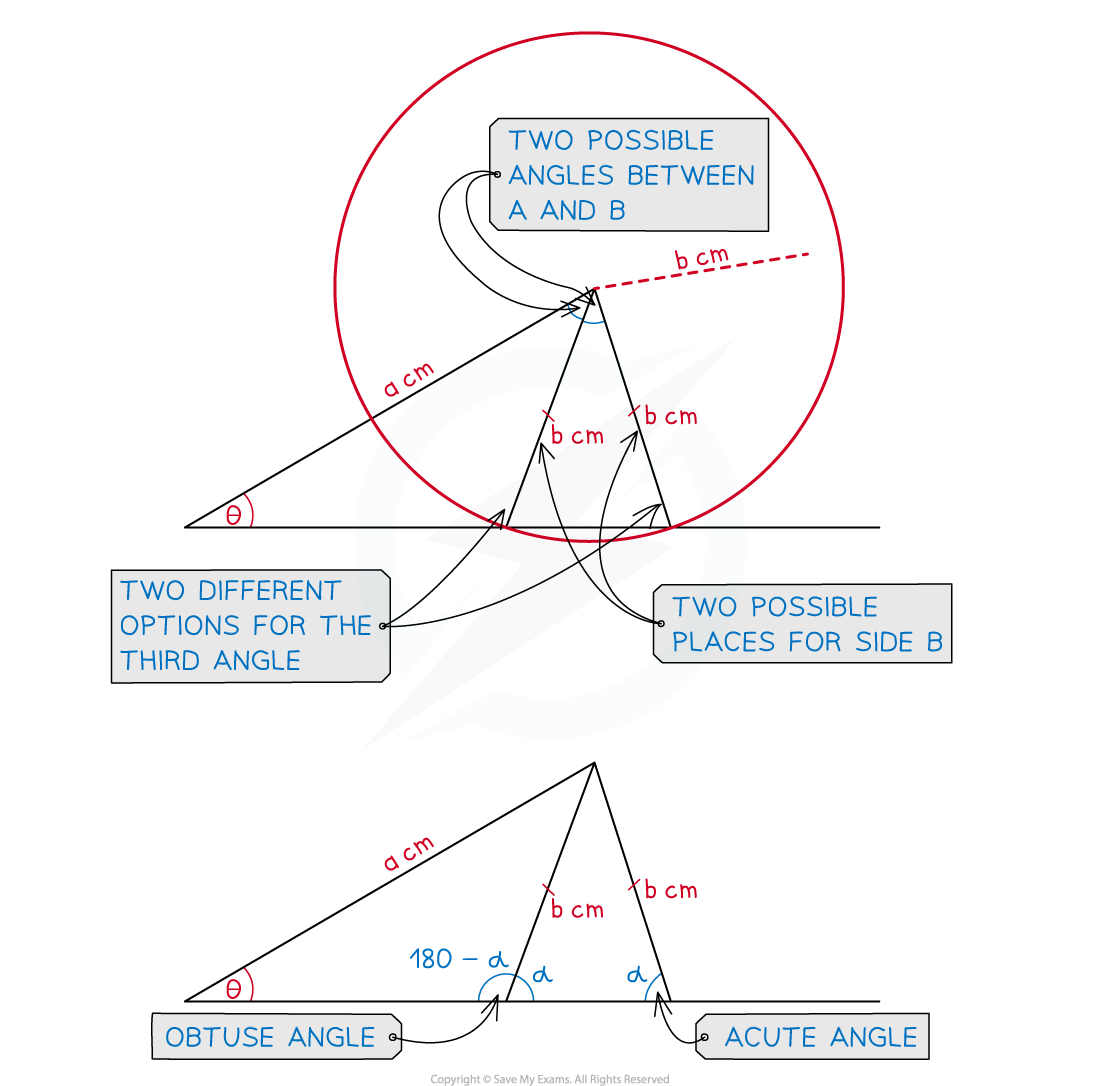
- If the sine rule is used in a triangle given two sides and an angle which is not the angle between them there may be more than one possible triangle which could be drawn
- The side opposite the given angle could be in two possible positions
- This will create two possible values for each of the missing angles and two possible lengths for the missing side
- The two angles found opposite the given side (not the ambiguous side) will add up to 180°
- In IB the question will usually tell you whether the angle you are looking for is acute or obtuse
- The sine rule will always give you the acute option but you can subtract from 180° to find the obtuse angle
- Sometimes the obtuse angle will not be valid
- It could cause the sum of the three interior angles of the triangle to exceed 180°
Exam Tip
- Make sure that you are clear which of the two answers is the one that is required and make sure that you communicate this clearly to the examiner by writing it on the answer line!
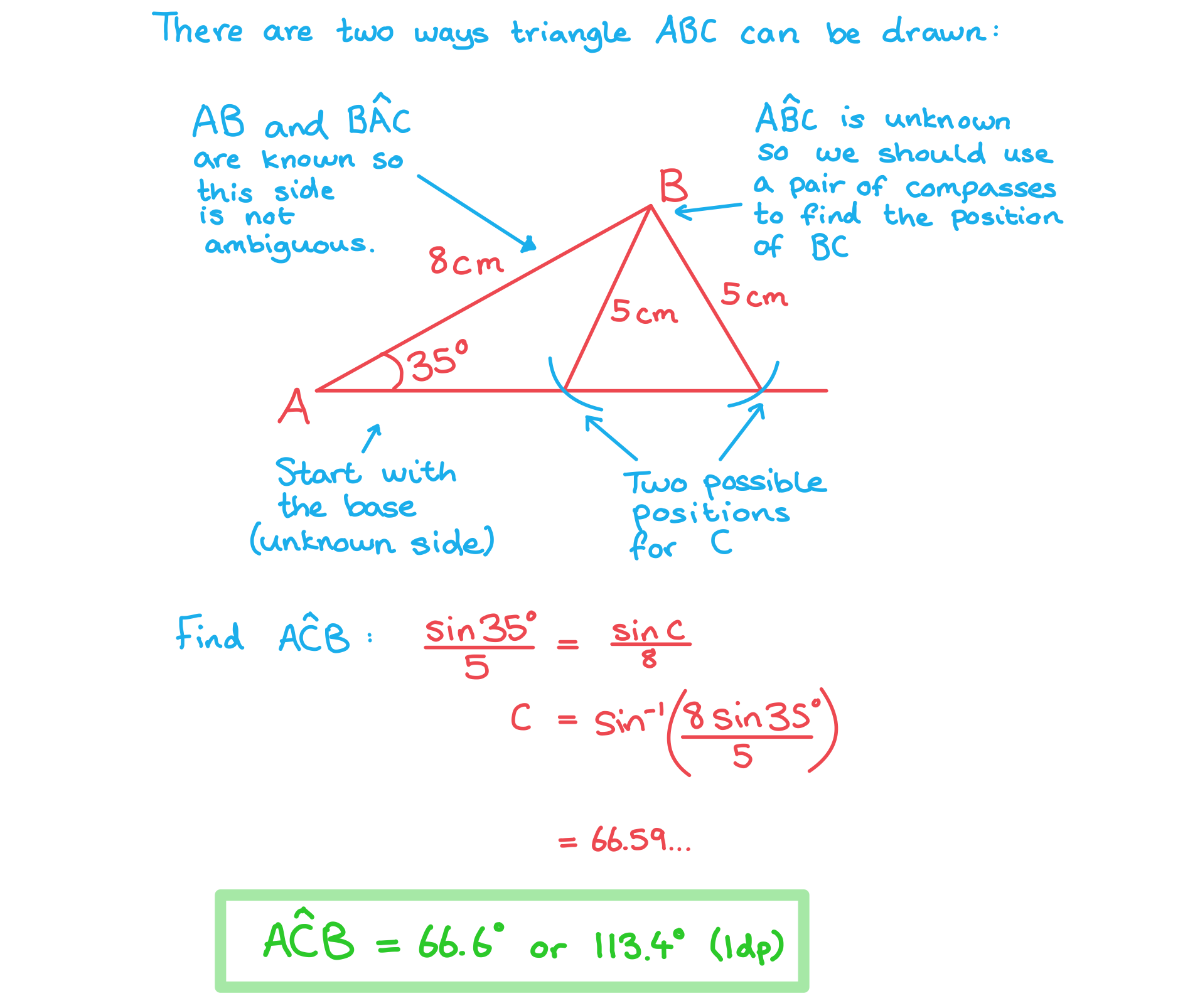
Worked Example
Cosine Rule
What is the cosine rule?
- The cosine rule allows us to find missing side lengths or angles in non-right-angled triangles
- It states that for any triangle
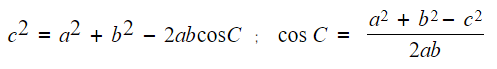
- Where
- c is the side opposite angle C
- a and b are the other two sides
- Both of these formulae are in the formula booklet, you do not need to remember them
- The first version is used to find a missing side
- The second version is a rearrangement of this and can be used to find a missing angle
- Cos 90° = 0 so if C = 90° this becomes Pythagoras’ Theorem
How can we use the cosine rule to find missing side lengths or angles?
- The cosine rule can be used when you have two sides and the angle between them or all three sides
- Always start by labelling your triangle with the angles and sides
- Remember the sides with the lower-case letters are opposite the angles with the equivalent upper-case letters
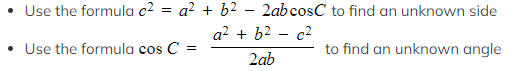 C is the angle between sides a and b
C is the angle between sides a and b
- Remember the sides with the lower-case letters are opposite the angles with the equivalent upper-case letters
- Substitute the values you have into the formula and solve
Exam Tip
- If you're using a calculator make sure that it is in the correct mode (degrees/radians)
- Remember to give your answers as exact values if you are asked too
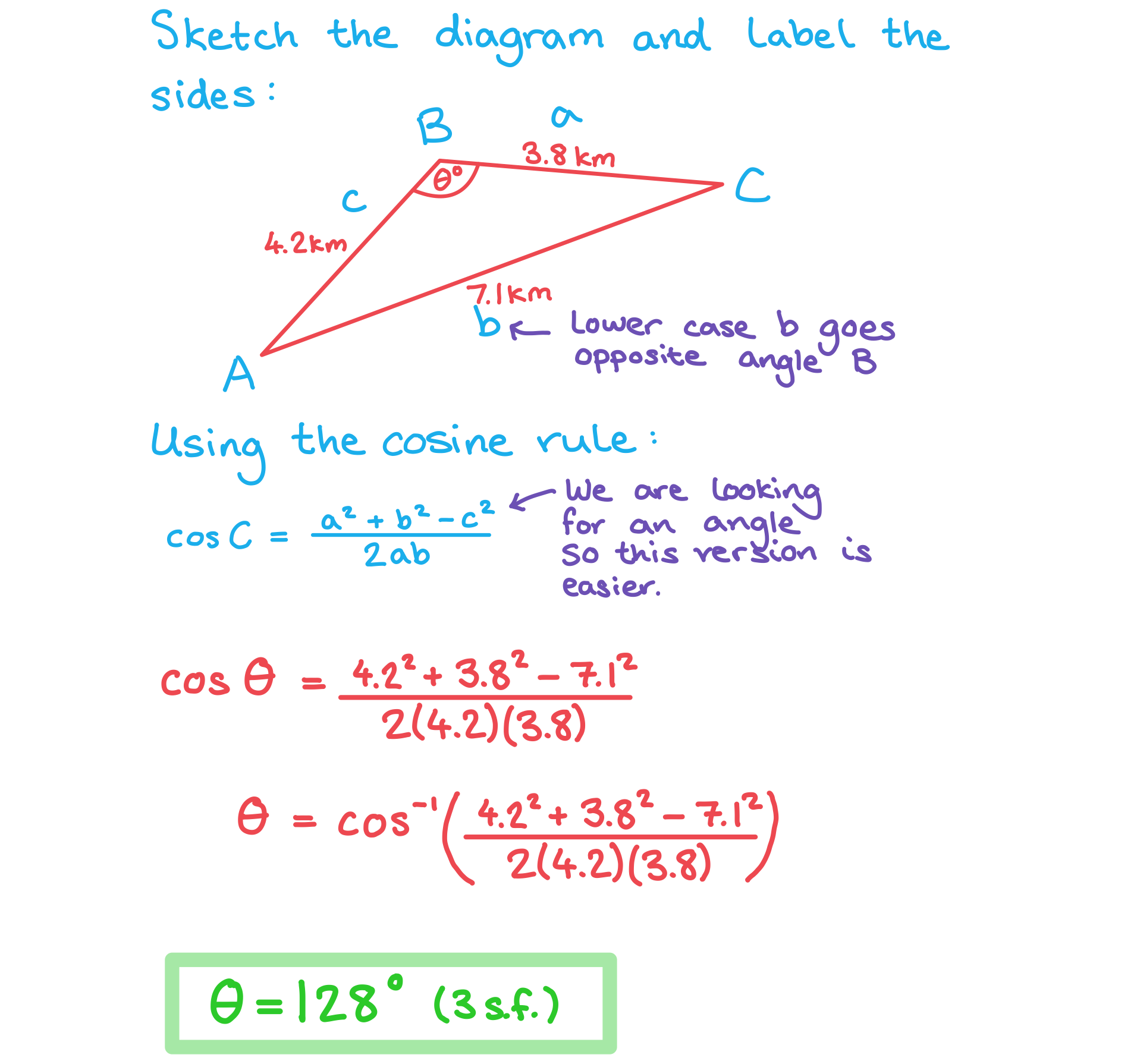
Worked Example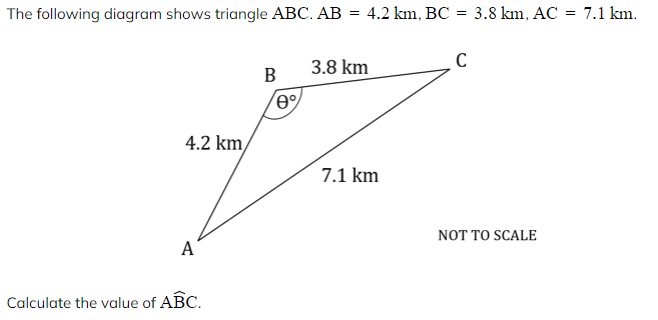
Area of a Triangle
How do I find the area of a non-right triangle?
- The area of any triangle can be found using the formula
-
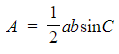 Where C is the angle between sides a and b
Where C is the angle between sides a and b
-
- This formula is in the formula booklet, you do not need to remember it
- Be careful to label your triangle correctly so that C is always the angle between the two sides
- Sin 90° = 1 so if C = 90° this becomes Area = ½ × base × height
Exam Tip
- If you're using a calculator make sure that it is in the correct mode (degrees/radians)
- Remember to give your answers as exact values if you are asked too
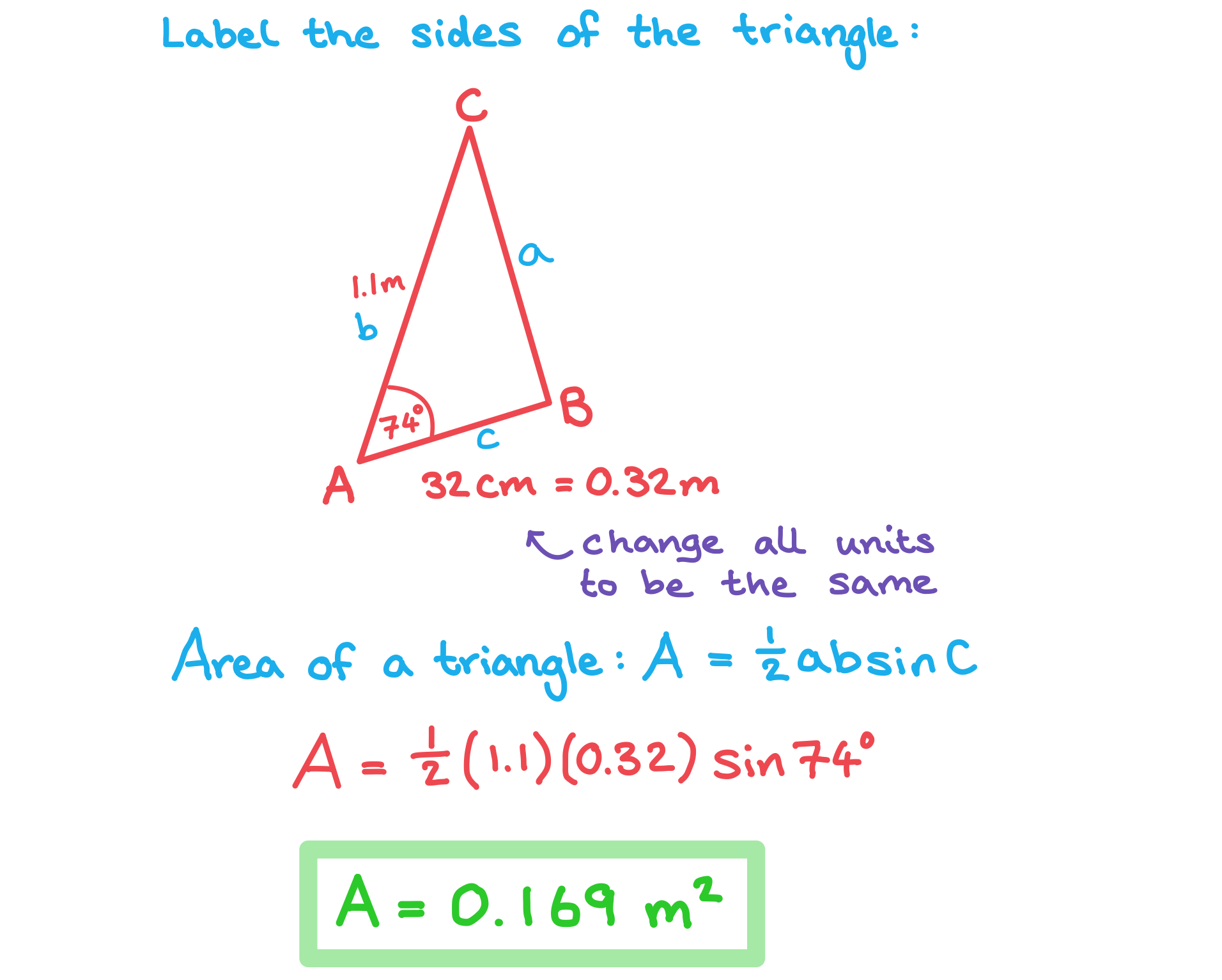
Worked Example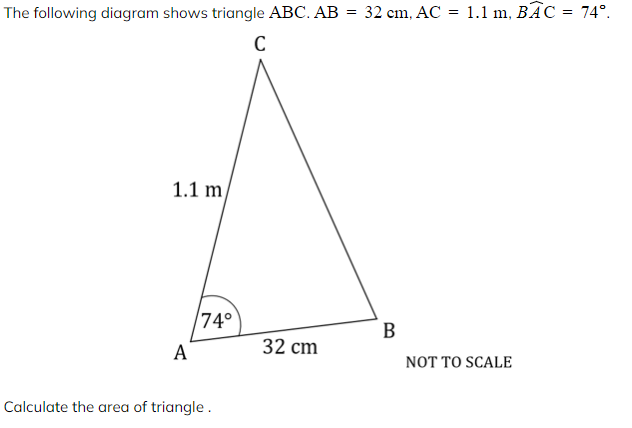
转载自savemyexams

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








