- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Maths: AI HL复习笔记3.1.1 Coordinate Geometry
Basic Coordinate Geometry
What are cartesian coordinates?
- Cartesian coordinates are basically the x-y coordinate system
- They allow us to label where things are in a two-dimensional plane
- In the 2D cartesian system, the horizontal axis is labelled x and the vertical axis is labelled y
What can we do with coordinates?
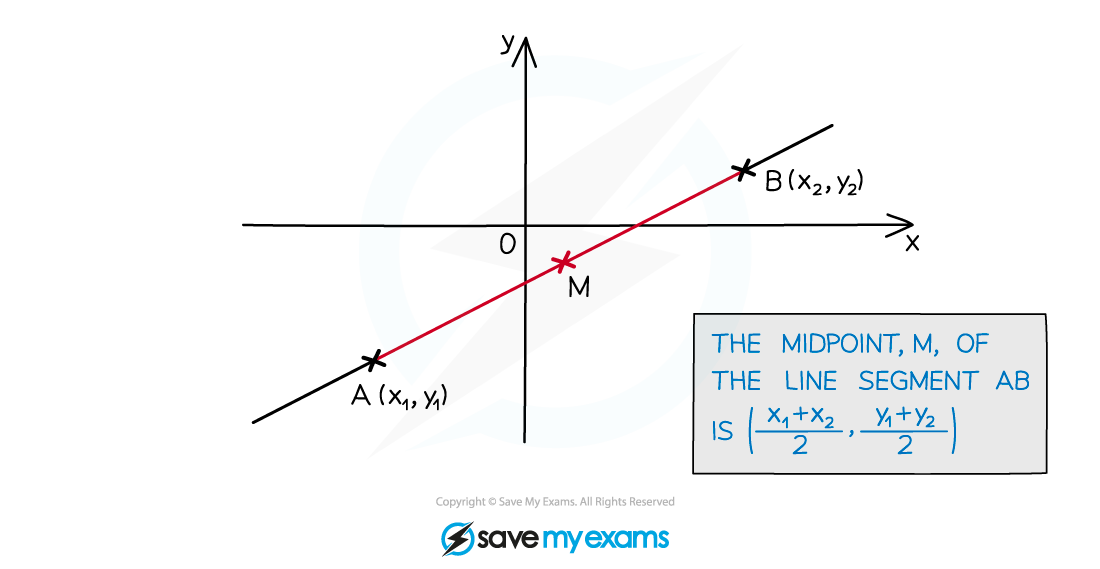
- If we have two points with coordinates (x1 , y1) and (x2 , y2) then we should be able to find
- The midpoint of the two points
- The distance between the two points
- The gradient of the line between them
How do I find the midpoint of two points?
- The midpoint is the average (middle) point
- It can be found by finding the middle of the x-coordinates and the middle of the y-coordinates
- The coordinates of the midpoint will be
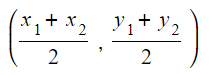
- This is given in the formula booklet under the prior learning section at the beginning
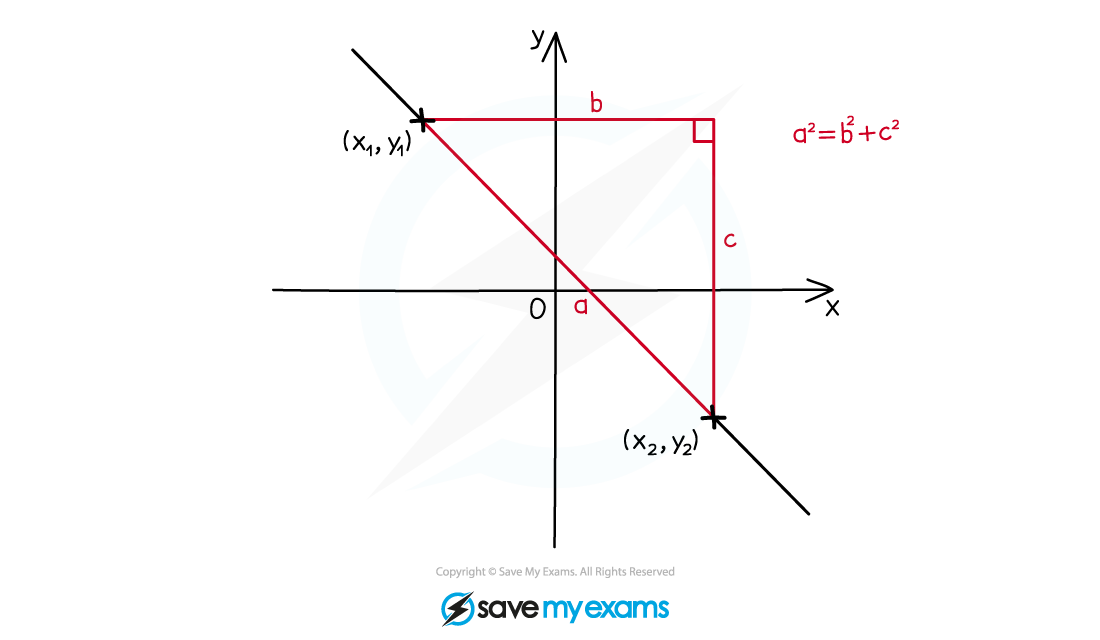
How do I find the distance between two points?
- The distance between two points with coordinates (x1 , y1) and (x2 , y2) can be found using the formula
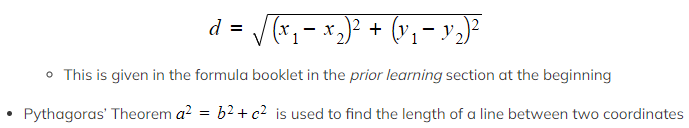 If the coordinates are labelled A and B then the line segment between them is written with the notation [AB]
If the coordinates are labelled A and B then the line segment between them is written with the notation [AB]
How do I find the gradient of the line between two points?
- The gradient of a line between two points with coordinates (x1 , y1) and (x2 , y2) can be found using the formula
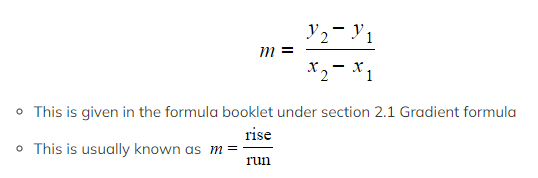
Worked Example
Point A has coordinates (3, 4) and point B has coordinates (-5, 2).
i)Calculate the distance of the line segment AB.

ii)Find the gradient of the line connecting points A and B.

iii)Find the midpoint of [AB ] .

Perpendicular Bisectors
What is a perpendicular bisector?
- A perpendicular bisector of a line segment cuts the line segment in half at a right angle
- Perpendicular lines meet at right angles
- Bisector means to cut in half
- Two lines are perpendicular if the product of their gradients is -1
How do I find the equation of the perpendicular bisector of a line segment?
- To find the equation of a straight line you need to find
- The gradient of the line
- A coordinate of a point on the line
- To find the equation of the perpendicular bisector of a line segment follow these steps:
-
- STEP 1: Find the coordinates of the midpoint of the line segment
- We know that the perpendicular bisector will cut the line segment in half so we can use the midpoint of the line segment as the known coordinate on the bisector
- STEP 2: Find the gradient of the line segment
- STEP 1: Find the coordinates of the midpoint of the line segment
-
- STEP 3: Find the gradient of the perpendicular bisector
- This will be -1 divided by the gradient of the line segment
- STEP 3: Find the gradient of the perpendicular bisector
 Worked Example
Worked Example

转载自savemyexams

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








