- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Maths: AI HL复习笔记2.6.4 Piecewise Models
Linear Piecewise Models
What are the parameters of a piecewise linear model?
 For each linear model there will be
For each linear model there will be
- The rate of change for that interval mi
- The value if the independent variable was not present ci
What can be modelled as a piecewise linear model?
- Piecewise linear models can be used when the rate of change of a function changes for different intervals
- These commonly apply when there are different tariffs or levels of charges
- Anything with a constant rate of change for set intervals
- C(d) is the taxi charge for a journey of d km
- The charge might double after midnight
- R(d) is the rental fee for a car used for d days
- The daily fee might triple if the car is rented over bank holidays
- s(t) is the speed of a car travelling for t seconds with constant acceleration
- The car might reach a maximum speed
- C(d) is the taxi charge for a journey of d km
What are possible limitations of a piecewise linear model?
- Linear models have a constant rate of change
- In real-life this might not be the case
- A function might increase (or decrease) gradually rather than at a constant rate
Exam Tip
- Make sure that you know how to plot a piecewise model on your GDC
Worked Example

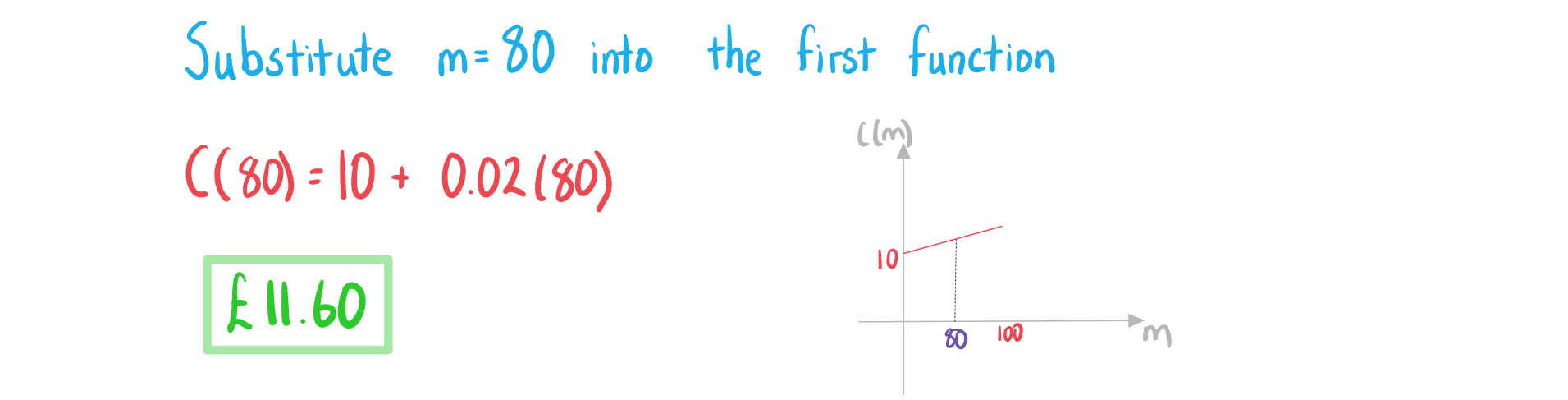
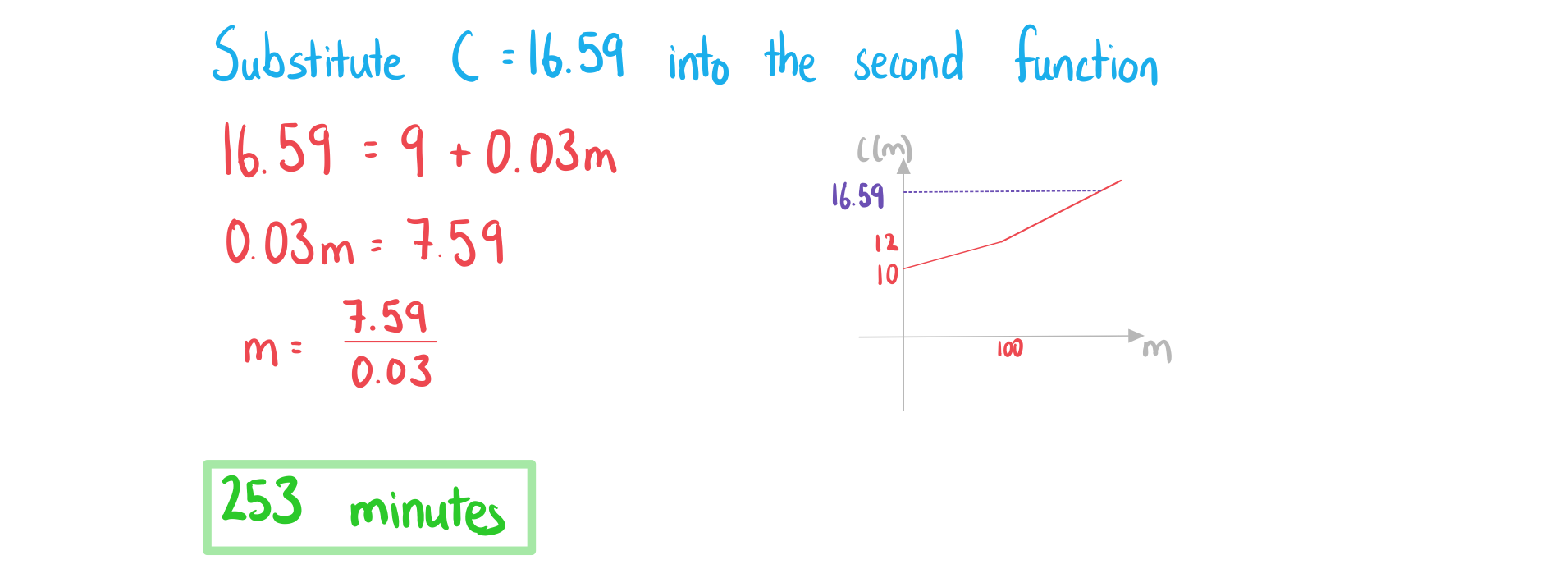
b)Given that the total monthly charge is £16.59, find the number of minutes that were used.
 Non-Linear Piecewise Models
Non-Linear Piecewise Models
What are the parameters of non-linear piecewise models?
 What can be modelled as a non-linear piecewise model?
What can be modelled as a non-linear piecewise model?
- Piecewise models can be used when different functions are needed to represent the output for different intervals of the variable
- S(x) is the standardised score on a test with x raw marks
- For small values of x there might be a quadratic model
- For large values of x there might be a linear model
- H(t) is the height of water in a bathtub with after t minutes
- Initially a cubic model might be a appropriate if the bottom of the bathtub is curved
- Then a linear model might be a appropriate if the sides of top of the bathtub has the shape of a prism
- S(x) is the standardised score on a test with x raw marks
What are possible limitations a non-linear piecewise model?
- Piecewise models can be used to model real-life accurately
- Piecewise models can be difficult to analyse or apply mathematical techniques to
Exam Tip
- Read and re-read the question carefully, try to get involved in the context of the question!
- Pay particular attention to the domain of each section, if it is not given think carefully about any restrictions there may be as a result of the context of the question
- If sketching a piecewise function, make sure to include the coordinates of all key points including the point at which two sections of the piecewise model meet
Worked Example
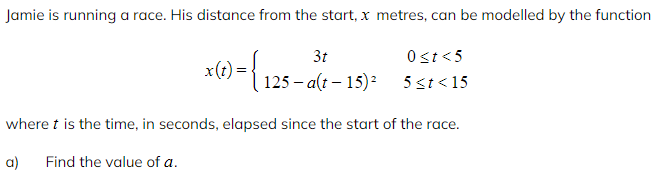
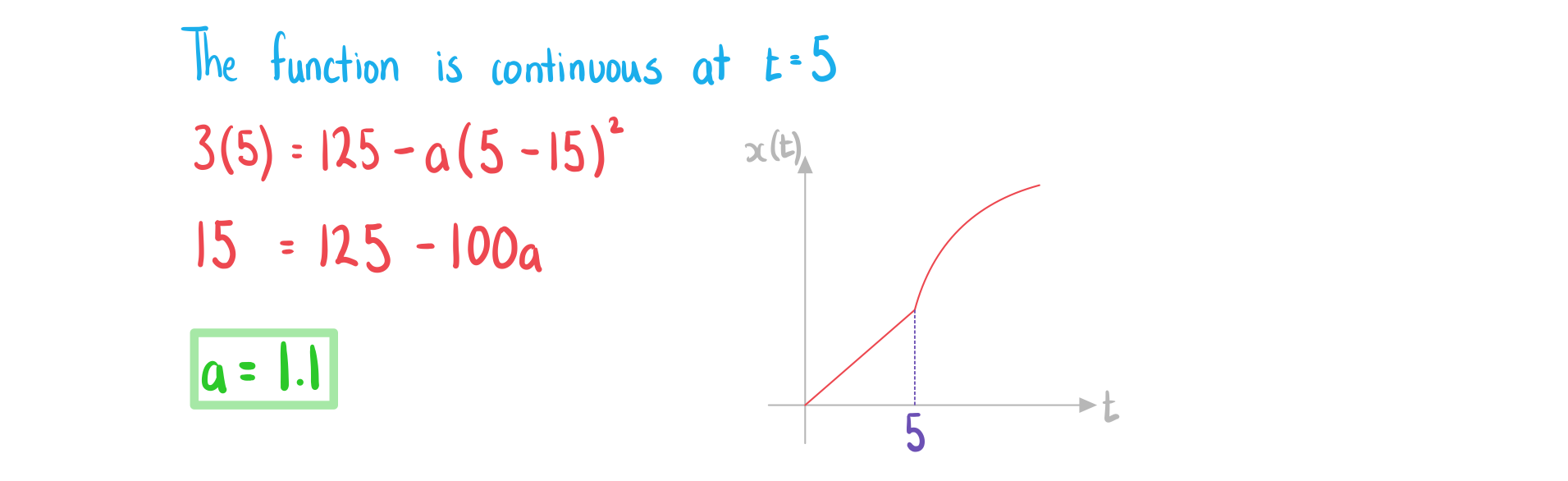
b)Find the time taken for Jamie to reach 100 metres from the start.
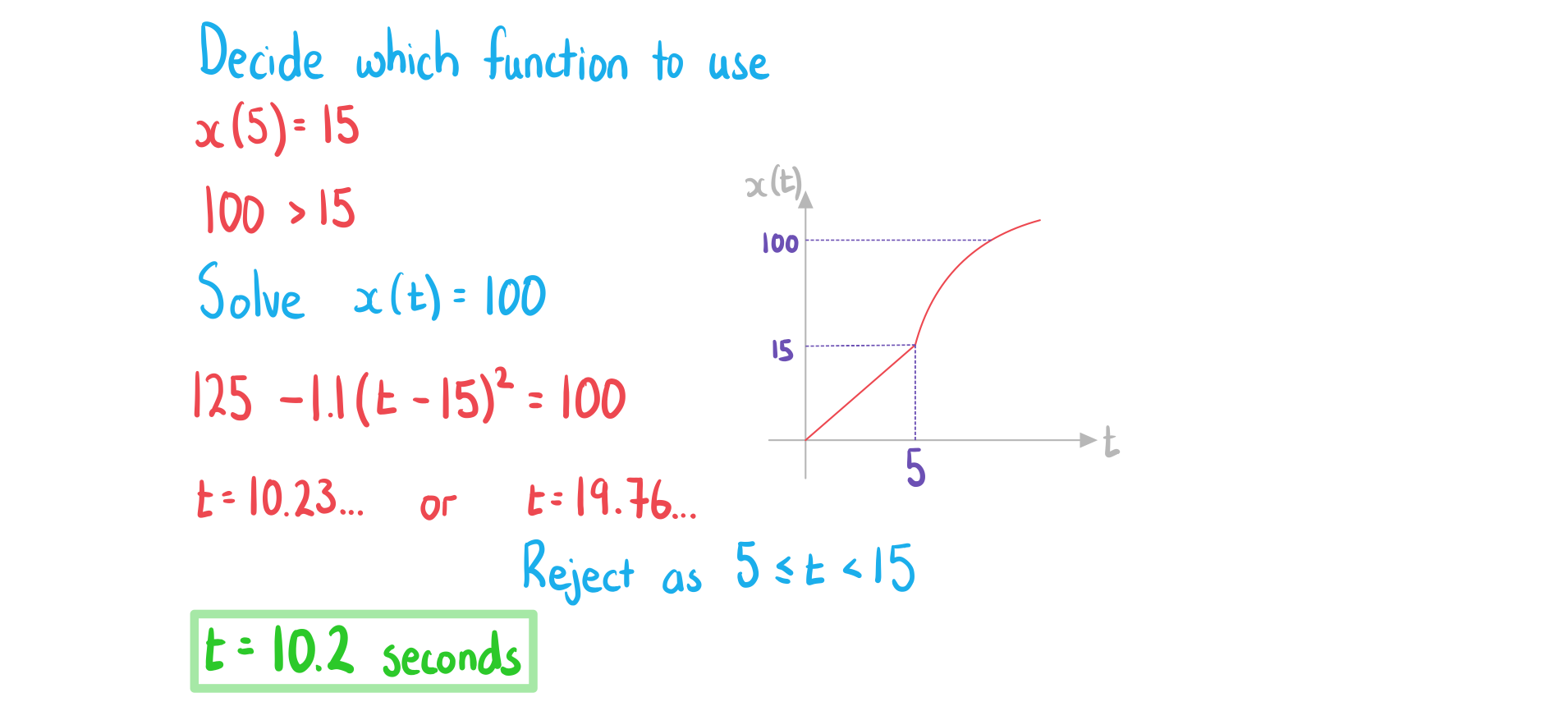
转载自savemyexams

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








