IB DP Maths: AI HL复习笔记2.3.1 Linear Models
Linear Models
What are the parameters of a linear model?
The m represents the rate of change of the function
- This is the amount the function increases/decreases when x increases by 1
- If the function is increasing m is positive
- If the function is decreasing m is negative
- When the model is represented as a graph this is the gradient of the line
- This is the amount the function increases/decreases when x increases by 1
- The c represents the value of the function when x = 0
- This is the value of the function when the independent variable is not present
- This is usually referred to as the initial value
- When the model is represented as a graph this is the y-intercept of the line
What can be modelled as a linear model?
- If the graph of the data resembles a straight line
- Anything with a constant rate of change
- C(d) is the taxi charge for a journey of d km
- B(m) is the monthly mobile phone bill when m minutes have been used
- R(d) is the rental fee for a car used for d days
- d(t) is the distance travelled by a car moving at a constant speed for t seconds
What are possible limitations of a linear model?
- Linear models continuously increase (or decrease) at the same rate
- In real-life this might not be the case
- The function might reach a maximum (or minimum)
- If the value of m is negative then for some inputs the function will predict negative values
- In some real-life situations negative values will not make sense
- To overcome this you can decide on an appropriate domain so that the outputs are never negative
Exam Tip
- Make sure that you are equally confident in working with linear models both algebraically and graphically as it may be easier using one method over the other when tackling a particular exam question
Worked Example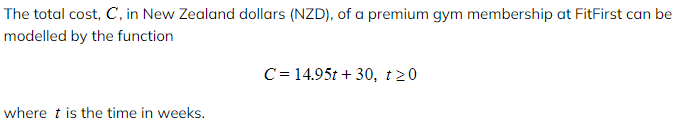
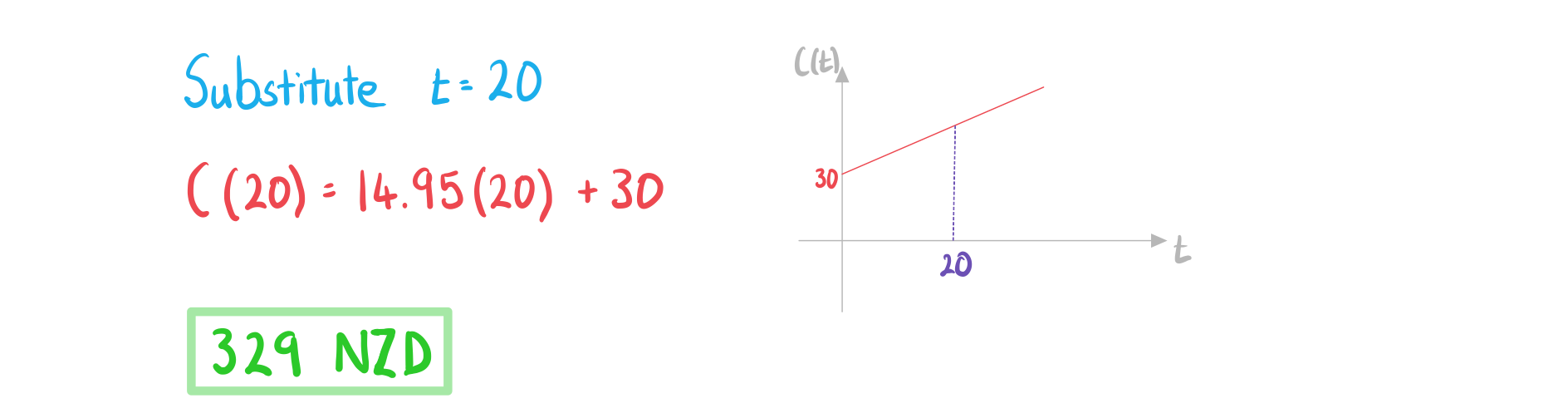
a)Calculate the cost of the gym membership for 20 weeks.
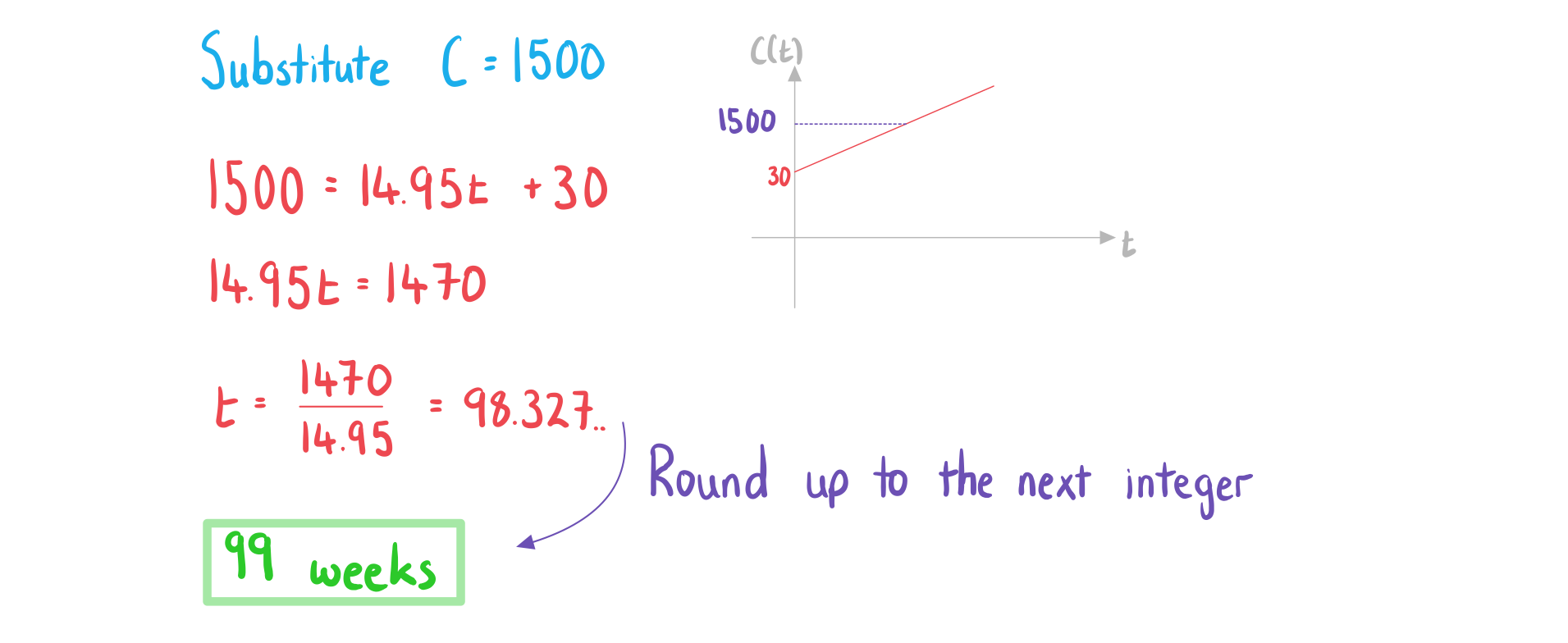
b)Find the number of weeks it takes for the total cost to exceed 1500 NZD.
c)Under new management, FitFirst changes the initial payment to 20 NZD and the weekly cost to 19.25 NZD. Write the new cost function after these changes have been.
转载自savemyexams
国际竞赛真题资料-点击免费领取！
欧几里得竞赛 寒假集训班开课了！
AMC8备考管家服务全新上线！
