IB DP Maths: AI HL复习笔记1.6.2 Forms of Complex Numbers
Modulus-Argument (Polar) Form
How do I write a complex number in modulus-argument (polar) form?
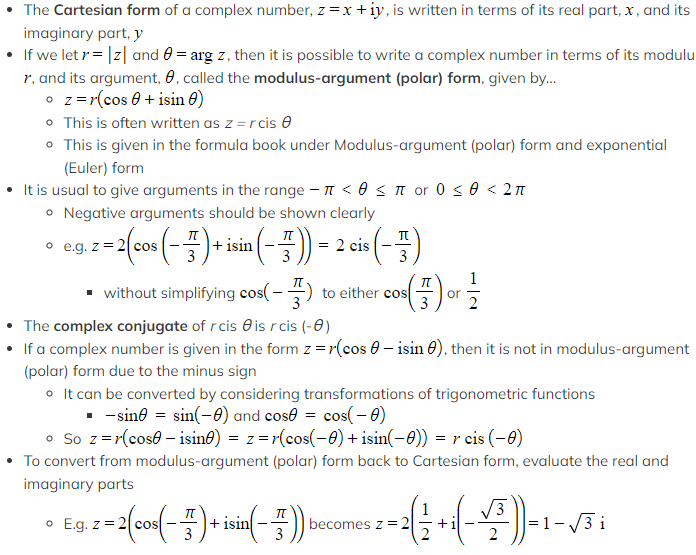How do I multiply complex numbers in modulus-argument (polar) form?
- The main benefit of writing complex numbers in modulus-argument (polar) form is that they multiply and divide very easily
How do I divide complex numbers in modulus-argument (polar) form?
- To divide two complex numbers in modulus-argument (polar) form, we divide their moduli and subtract their arguments
Exam Tip
Worked Example
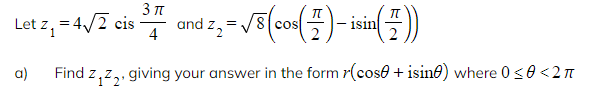
Exponential (Euler's) Form
How do we write a complex number in Euler's (exponential) form?
How do we multiply and divide complex numbers in Euler's form?
What are some common numbers in exponential form?
Exam Tip
- Euler's form allows for easy manipulation of complex numbers, in an exam it is often worth the time converting a complex number into Euler's form if further calculations need to be carried out
- Familiarise yourself with which calculations are easier in which form, for example multiplication and division are easiest in Euler's form but adding and subtracting are easiest in Cartesian form
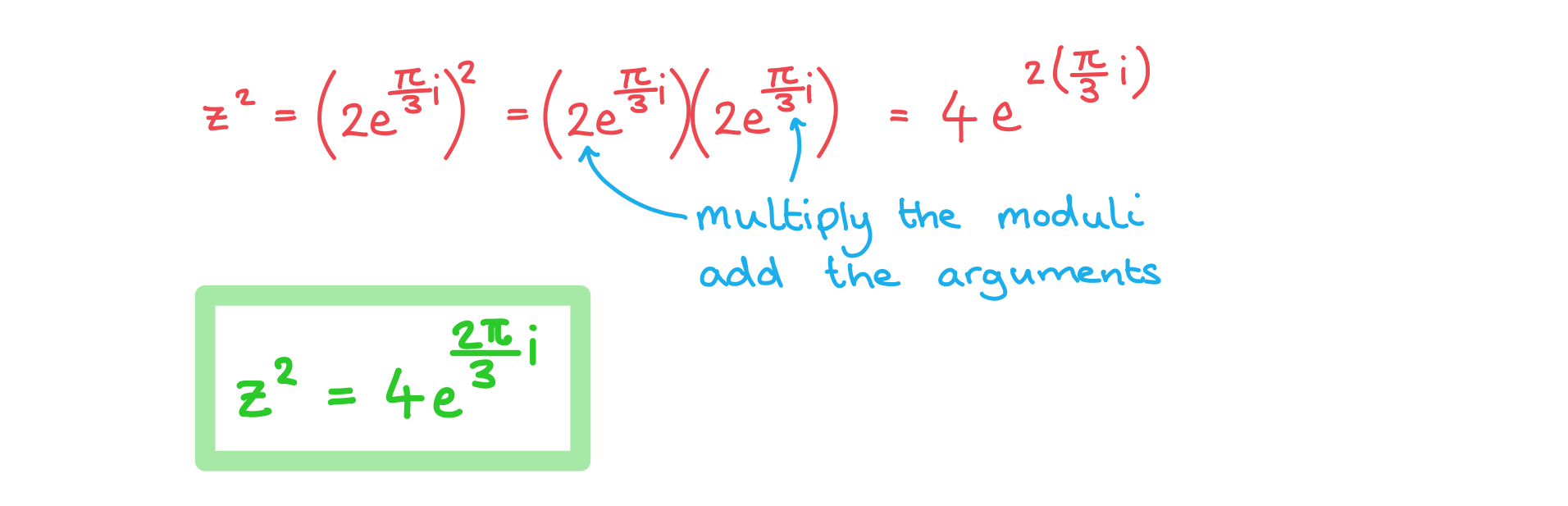
Worked Example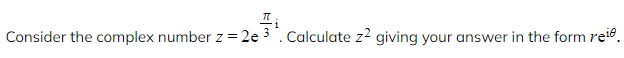
Conversion of Forms
Converting from Cartesian form to modulus-argument (polar) form or exponential (Euler's) form.
- To convert from Cartesian form to modulus-argument (polar) form or exponential (Euler) form use
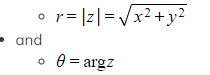Converting from modulus-argument (polar) form or exponential (Euler's) form to Cartesian form.
- To convert from modulus-argument (polar) form to Cartesian form
- Write z = r (cosθ+ isinθ)as z = r cosθ+ (r sinθ )i
- Find the values of the trigonometric ratios r sinθand r cosθ
- You may need to use your knowledge of trig exact values
- Rewrite as z = a + bi where
- a = r cosθ and b = r sinθ
- To convert from exponential (Euler’s) form to Cartesian form first rewrite z = r eiθin the form z = r cosθ+ (r sinθ)i and then follow the steps above
Exam Tip
- When converting from Cartesian form into Polar or Euler's form, always leave your modulus and argument as an exact value
- Rounding values too early may result in inaccuracies later on
Worked Example
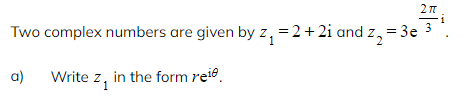
转载自savemyexams
国际竞赛真题资源免费领取
美高学分项目重磅来袭！立即了解
