- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Maths: AI HL复习笔记1.5.3 Introduction to Argand Diagrams
Argand Diagrams
What is the complex plane?
- The complex plane, sometimes also known as the Argand plane, is a two-dimensional plane on which complex numbers can be represented geometrically
- It is similar to a two-dimensional Cartesian coordinate grid
- The x-axis is known as the real axis (Re)
- The y-axis is known as the imaginary axis (Im)
- The complex plane emphasises the fact that a complex number is two dimensional
- i.e it has two parts, a real and imaginary part
- Whereas a real number only has one dimension represented on a number line (the x-axis only)
What is an Argand diagram?
- An Argand diagram is a geometrical representation of complex numbers on a complex plane
- A complex number can be represented as either a point or a vector
- The complex number x + yi is represented by the point with cartesian coordinate (x, y)
- The real part is represented by the point on the real (x-) axis
- The imaginary part is represented by the point on the imaginary (y-) axis
- Complex numbers are often represented as vectors
- A line segment is drawn from the origin to the cartesian coordinate point
- An arrow is added in the direction away from the origin
- This allows for geometrical representations of complex numbers
Exam Tip
- When setting up an Argand diagram you do not need to draw a fully scaled axes, you only need the essential information for the points you want to show, this will save a lot of time
Worked Example
a)Plot the complex numbers z1 = 2 + 2i and z2 = 3 – 4i as points on an Argand diagram.
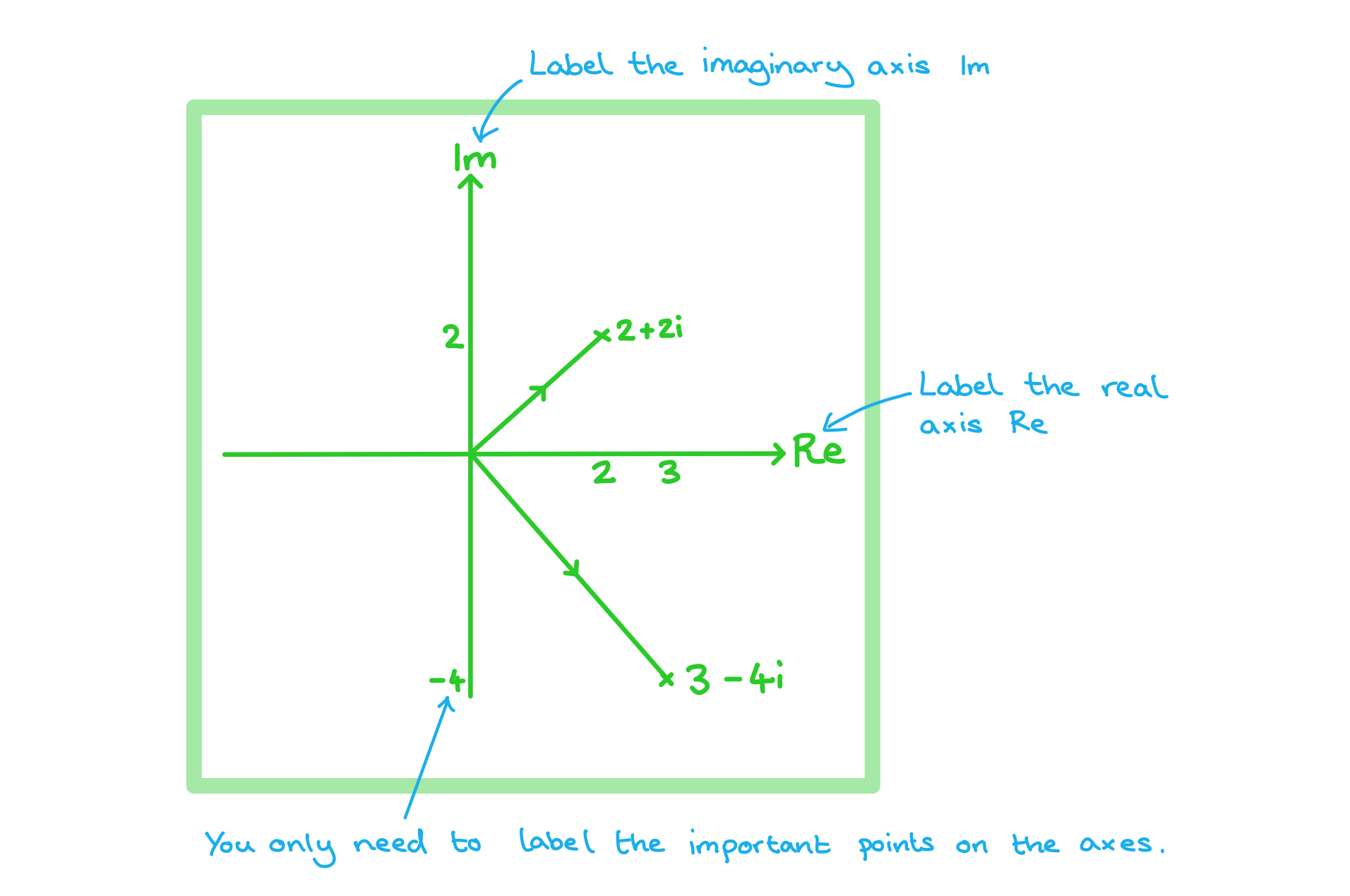
b)Write down the complex numbers represented by the points A and B on the Argand diagram below.

Complex Roots of Quadratics
What are complex roots?
- A quadratic equation can either have two real roots (zeros), a repeated real root or no real roots
- This depends on the location of the graph of the quadratic with respect to the x-axis
- If a quadratic equation has no real roots we would previously have stated that it has no real solutions
- The quadratic equation will have a negative discriminant
- This means taking the square root of a negative number
- Complex numbers provide solutions for quadratic equations that have no real roots
How do we solve a quadratic equation when it has complex roots?
- If a quadratic equation takes the form ax2+ bx + c = 0 it can be solved by either using the quadratic formula or completing the square
- If a quadratic equation takes the form ax2+ b = 0 it can be solved by rearranging
- The property i = √-1 is used
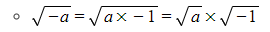 If the coefficients of the quadratic are real then the complex roots will occur in complex conjugate pairs
If the coefficients of the quadratic are real then the complex roots will occur in complex conjugate pairs
- If z = m + ni (n ≠ 0) is a root of a quadratic with real coefficients then z* = m - ni is also a root
- The real part of the solutions will have the same value as the x coordinate of the turning point on the graph of the quadratic
- When the coefficients of the quadratic equation are non-real, the solutions will not be complex conjugates
- To solve these you can use the quadratic formula
How do we factorise a quadratic equation if it has complex roots?
- If we are given a quadratic equation in the form az2+ bz + c = 0, where a, b, and c ∈ ℝ, a ≠ 0 we can use its complex roots to write it in factorised form
- Use the quadratic formula to find the two roots, z = p + qi and z*= p - qi
- This means that z – (p + qi) and z – (p – qi) must both be factors of the quadratic equation
- Therefore we can write az2+ bz + c = (z – (p + qi))( z – (p - qi))
- This can be rearranged into the form (z – p – qi)(z – p + qi)
Exam Tip
 Worked Example
Worked Example
Solve the quadratic equation z2 - 2z + 5 = 0 and hence, factorise z2 - 2z + 5.

转载自savemyexams


最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








