- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
IB DP Maths: AI HL复习笔记1.3.3 Geometric Sequences & Series
Geometric Sequences
What is a geometric sequence?
- In a geometric sequence, there is a common ratio, r, between consecutive terms in the sequence
- For example, 2, 6, 18, 54, 162, … is a sequence with the rule ‘start at two and multiply each number by three’
- The first term, u1, is 2
- The common ratio, r, is 3
- For example, 2, 6, 18, 54, 162, … is a sequence with the rule ‘start at two and multiply each number by three’
- A geometric sequence can be increasing (r > 1) or decreasing (0 < r < 1)
- If the common ratio is a negative number the terms will alternate between positive and negative values
- For example, 1, -4, 16, -64, 256, … is a sequence with the rule ‘start at one and multiply each number by negative four’
-
- The first term, u1, is 1
- The common ratio, r, is -4
-
- For example, 1, -4, 16, -64, 256, … is a sequence with the rule ‘start at one and multiply each number by negative four’
- Each term of a geometric sequence is referred to by the letter u with a subscript determining its place in the sequence
How do I find a term in a geometric sequence?
-
 This formula allows you to find any term in the geometric sequence
This formula allows you to find any term in the geometric sequence- It is given in the formula booklet, you do not need to know how to derive it
- Enter the information you have into the formula and use your GDC to find the value of the term
- Sometimes you will be given a term and asked to find the first term or the common ratio
- Substitute the information into the formula and solve the equation
- You could use your GDC for this
- Substitute the information into the formula and solve the equation
- Sometimes you will be given two or more consecutive terms and asked to find both the first term and the common ratio
- Find the common ratio by dividing a term by the one before it
- Substitute this and one of the terms into the formula to find the first term
- Sometimes you may be given a term and the formula for the nth term and asked to find the value of n
- You can solve these using logarithms on your GDC
Exam Tip
- You will sometimes need to use logarithms to answer geometric sequences questions
- Make sure you are confident doing this
- Practice using your GDC for different types of questions
Worked Example


![]()

Geometric Series
How do I find the sum of a geometric series?
- A geometric series is the sum of a certain number of terms in a geometric sequence
- For the geometric sequence 2, 6, 18, 54, … the geometric series is 2 + 6 + 18 + 54 + …
- The following formulae will let you find the sum of the first n terms of a geometric series:

- A question will often give you the sum of a certain number of terms and ask you to find the value of the first term, the common ratio, or the number of terms within the sequence
- Substitute the information into the formula and solve the equation
- You could use your GDC for this
- Substitute the information into the formula and solve the equation
Exam Tip
- The geometric series formulae are in the formulae booklet, you don't need to memorise them
- Make sure you can locate them quickly in the formula booklet
Worked Example
![]()

Sum to Infinity
What is the sum to infinity of a geometric series?
- A geometric sequence will either increase or decrease away from zero or the terms will get progressively closer to zero
- Terms will get closer to zero if the common ratio, r, is between 1 and -1
- If the terms are getting closer to zero then the series is said to converge
-
- This means that the sum of the series will approach a limiting value
- As the number of terms increase, the sum of the terms will get closer to the limiting value
How do we calculate the sum to infinity?
 Exam Tip
Exam Tip
- Learn and remember the conditions for when a sum to infinity can be calculated
Worked Example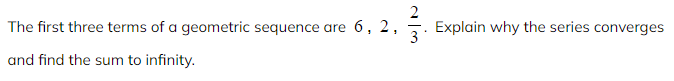

转载自savemyexams

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









