IB DP Maths: AA SL复习笔记5.4.4 Further Applications of Integration
Negative Integrals
How do I find the area under a curve when the curve is fully under the x-axis?
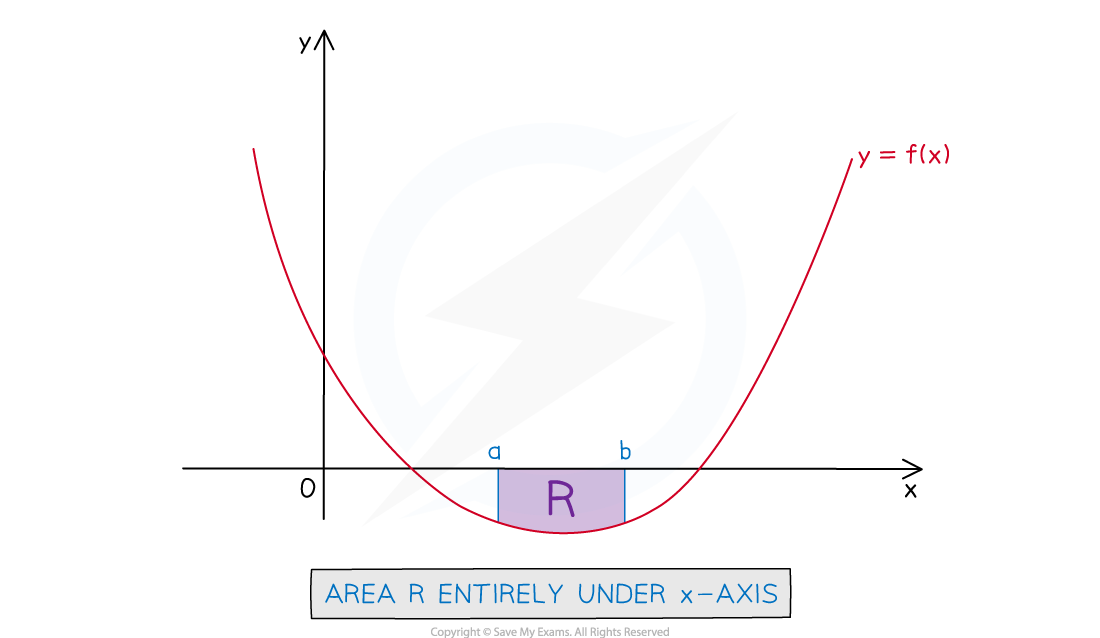
STEP 1
Write the expression for the definite integral to find the area as usual
This may involve finding the lower and upper limits from a graph sketch or GDC and f(x) may need to be rewritten in an integrable form
STEP 2
The answer to the definite integral will be negative
Area must always be positive so take the modulus (absolute value) of it
How do I find the area under a curve when the curve is partially under the x-axis?
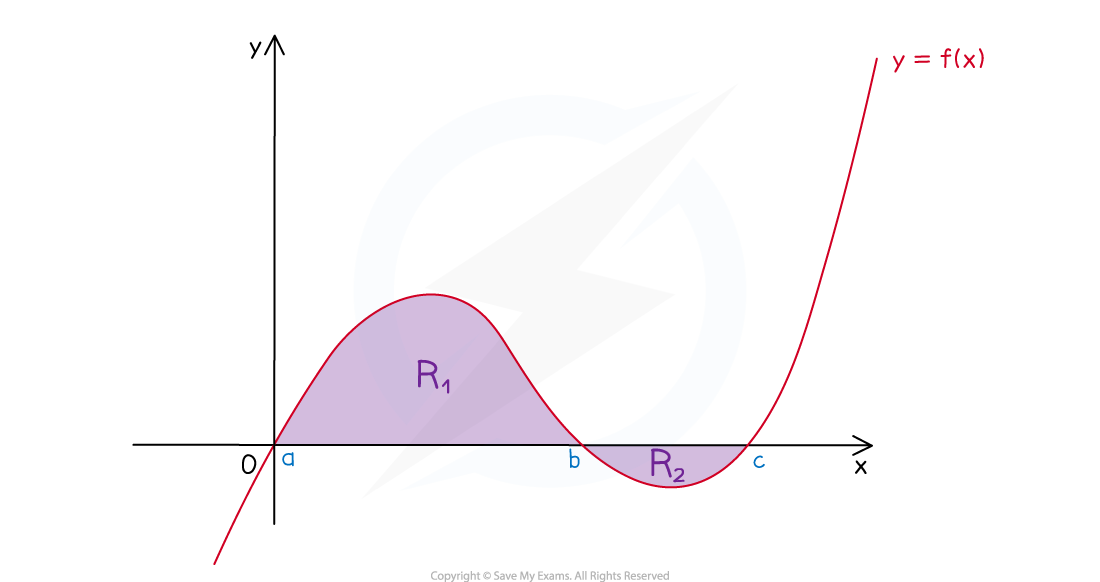
- For questions that allow the use of a GDC you can still use
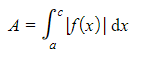To find the area analytically (manually) use the following method
STEP 1
Split the area into parts - the area(s) that are above the x-axis and the area(s) that are below the x-axis
Exam Tip
- If no diagram is provided, quickly sketch one so that you can see where the curve is above and below the x - axis and split up your integrals accordingly
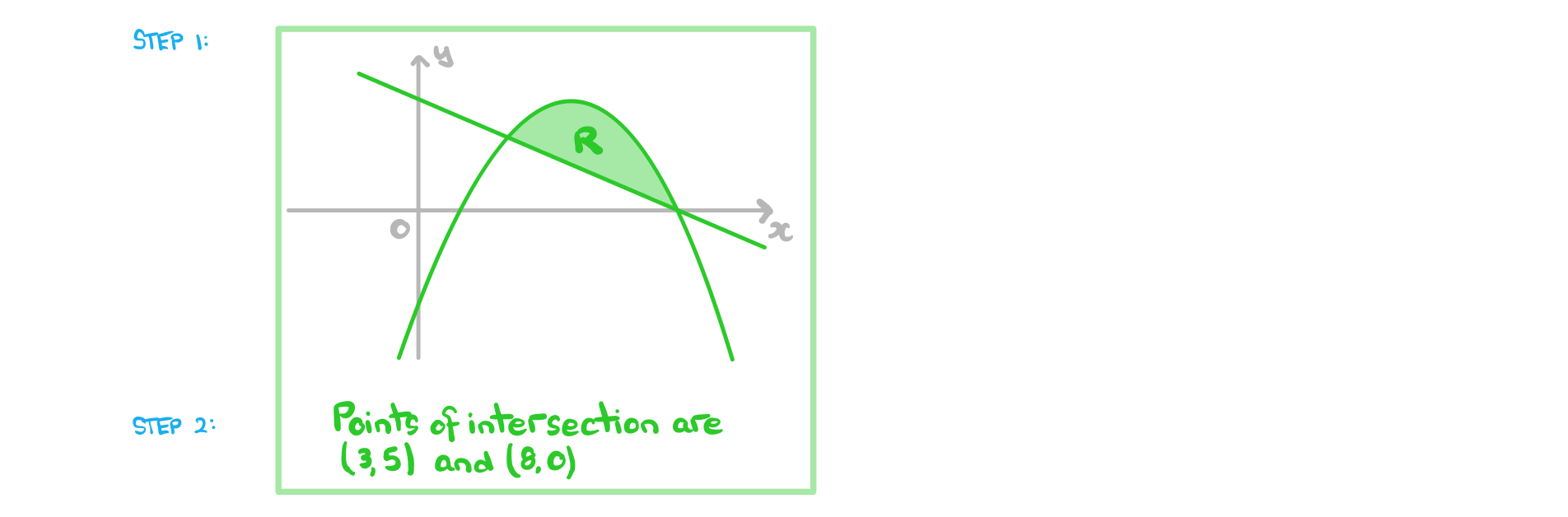
Worked Example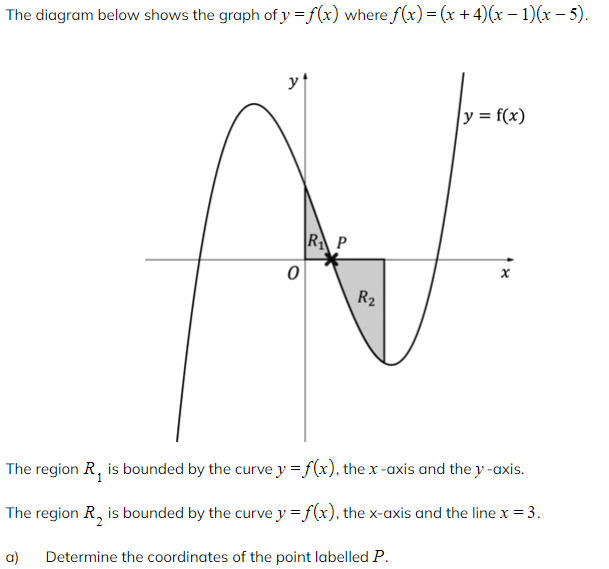
Area Between a Curve and a Line
- Areas whose boundaries include a curve and a (non-vertical) straight line can be found using integration
- For an area under a curve a definite integral will be needed
- For an area under a line the shape formed will be a trapezium or triangle
- basic area formulae can be used rather than a definite integral
- (although a definite integral would still work)
- The area required could be the sum or difference of areas under the curve and line
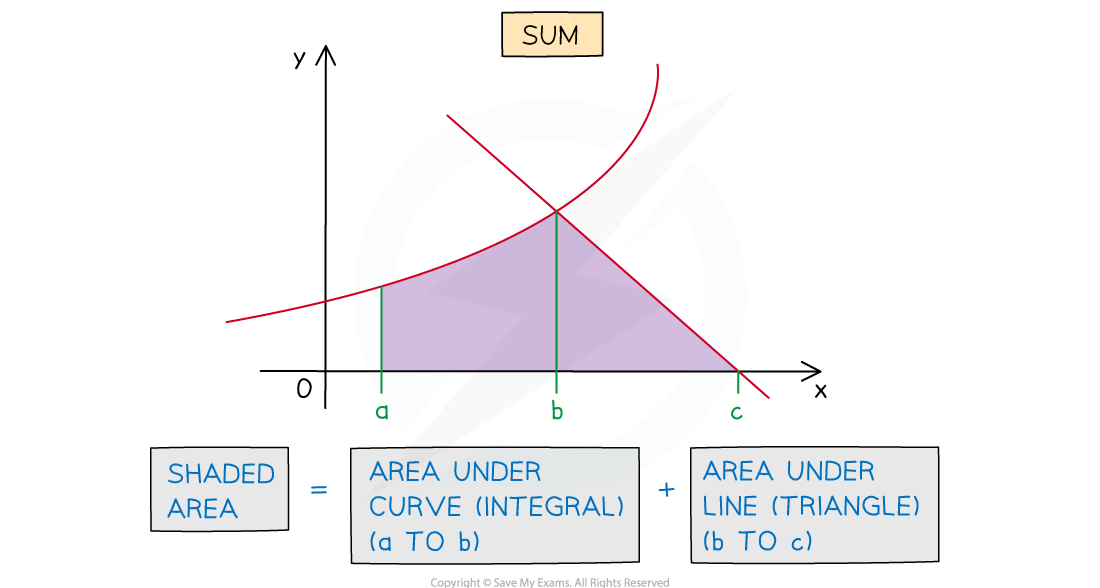
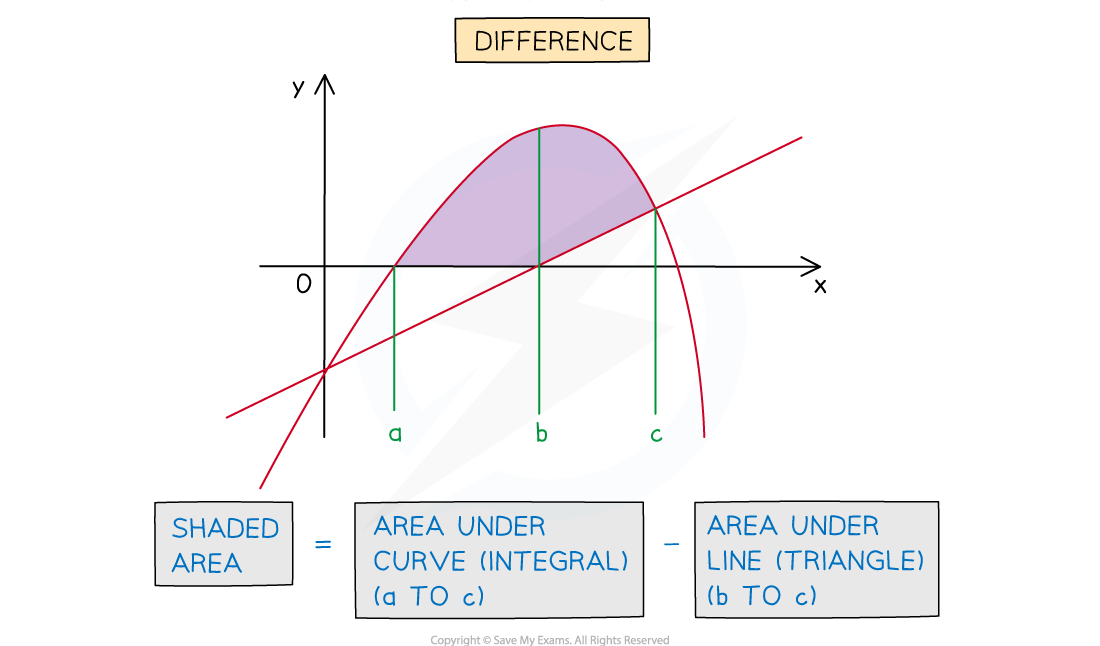
How do I find the area between a curve and a line?
STEP 1
If not given, sketch the graphs of the curve and line on the same diagram
Use a GDC to help with this step
STEP 2
Find the intersections of the curve and the line
If no diagram is given this will help identify the area(s) to be found
STEP 3
Determine whether the area required is the sum or difference of the area under the curve and the area under the line
Calculate the area under a curve using a integral of the form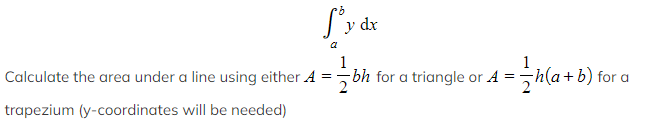
Calculate the area under a curve using a integral of the form
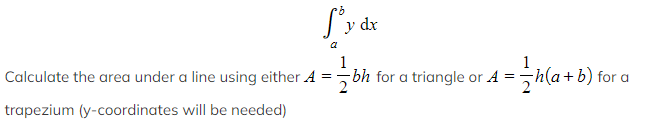
STEP 4
Evaluate the definite integrals and find their sum or difference as necessary to obtain the area required
Exam Tip
- Add information to any diagram provided
- Add axes intercepts, as well as intercepts between lines and curves
- Mark and shade the area you’re trying to find
- If no diagram is provided, sketch one!
Worked Example
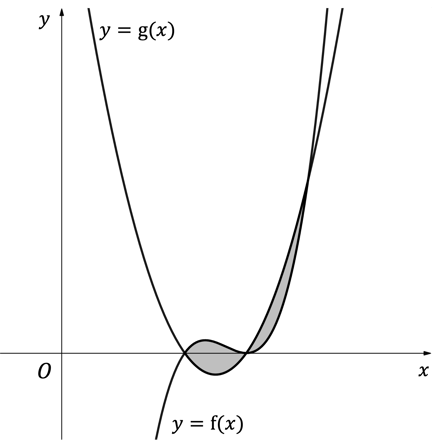
Area Between 2 Curves
- Areas whose boundaries include two curves can be found by integration
- The area between two curves will be the difference of the areas under the two curves
- both areas will require a definite integral
- Finding points of intersection may involve a more awkward equation than solving for a curve and a line
- The area between two curves will be the difference of the areas under the two curves
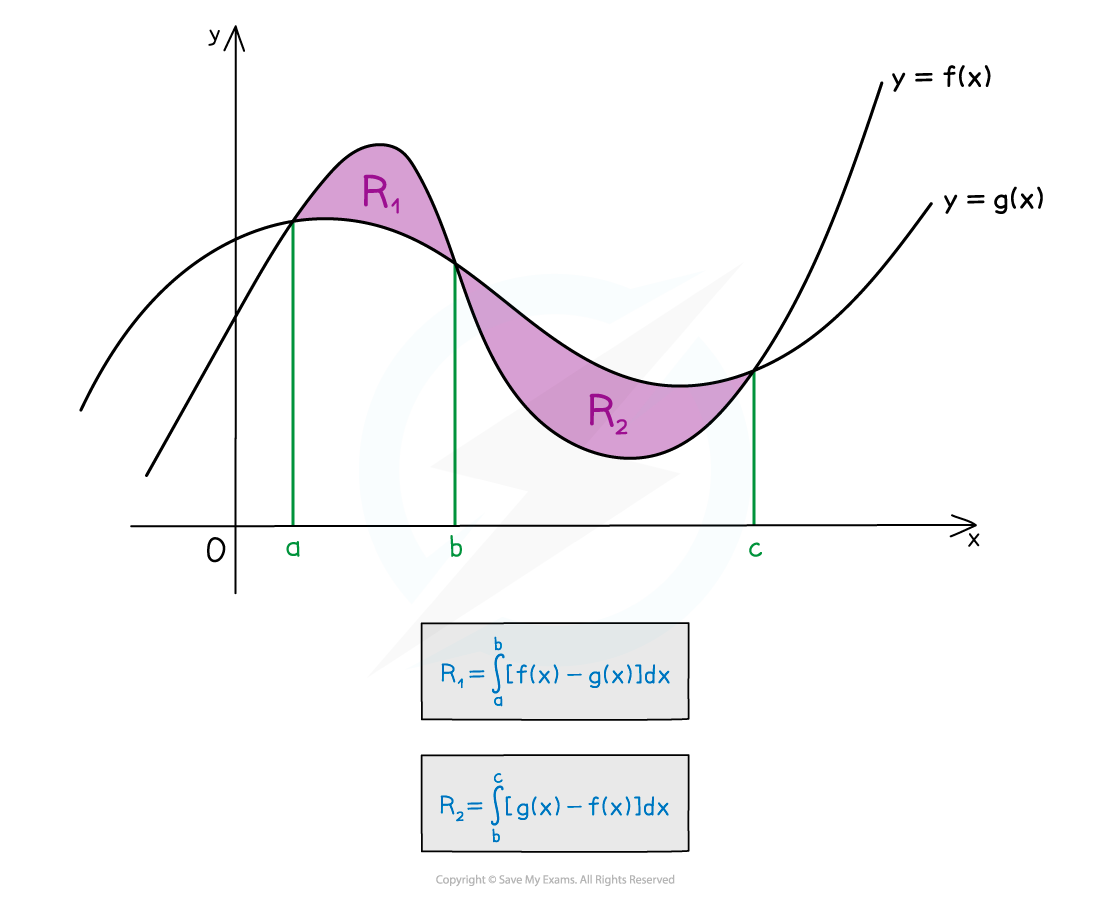
How do I find the area between two curves?
STEP 1
If not given, sketch the graphs of both curves on the same diagram
Use a GDC to help with this step
STEP 2
Find the intersections of the two curves
If no diagram is given this will help identify the area(s) to be found
STEP 4Evaluate the definite integrals and sum them up to find the total area
(Step 3 means no definite integral will have a negative value)
Exam Tip
- If no diagram is provided sketch one, even if the curves are not accurate
- Add information to any given diagram as you work through a question
- Maximise use of your GDC to save time and maintain accuracy:
- Use it to sketch the graphs and help you visualise the problem
- Use it to find definite integrals
Worked Example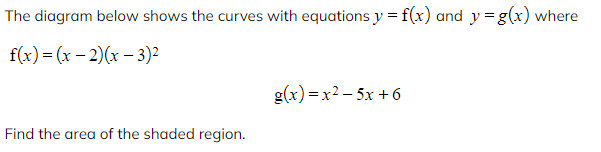
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
2025欧几里得数学竞赛报名开启！
