IB DP Maths: AA SL复习笔记5.4.2 Techniques of Integration
Integrating Composite Functions (ax+b)
What is a composite function?
- A composite function involves one function being applied after another
- A composite function may be described as a “function of a function”
How do I integrate linear (ax+b) functions?
Exam Tip
- Although the specific formulae in this revision note aren't given to you in the formula booklet, they can all be derived from the reverse chain rule (see below)
- The formula booklet contains almost all of the information you will need to apply to reverse chain rule and derive these in the exam, make sure you have it open on the right pages whilst you are working
Worked Example
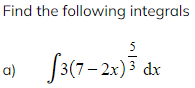
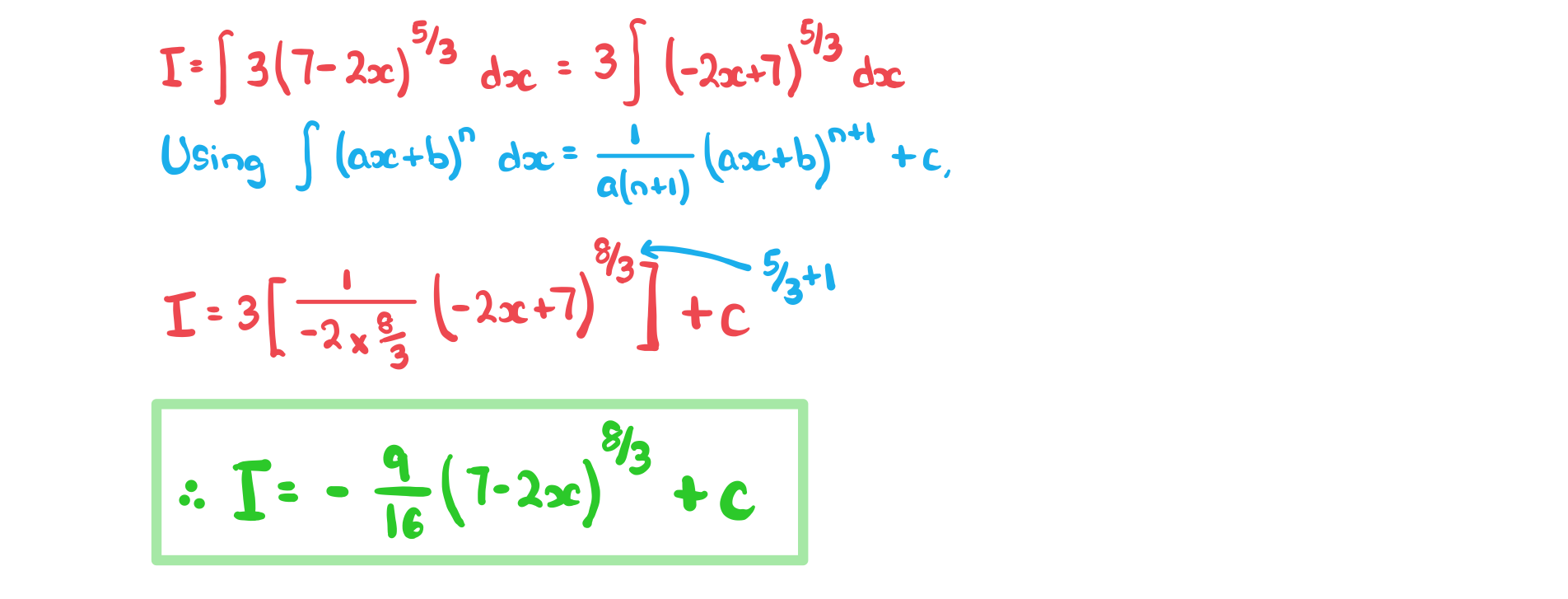
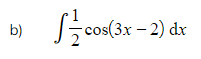
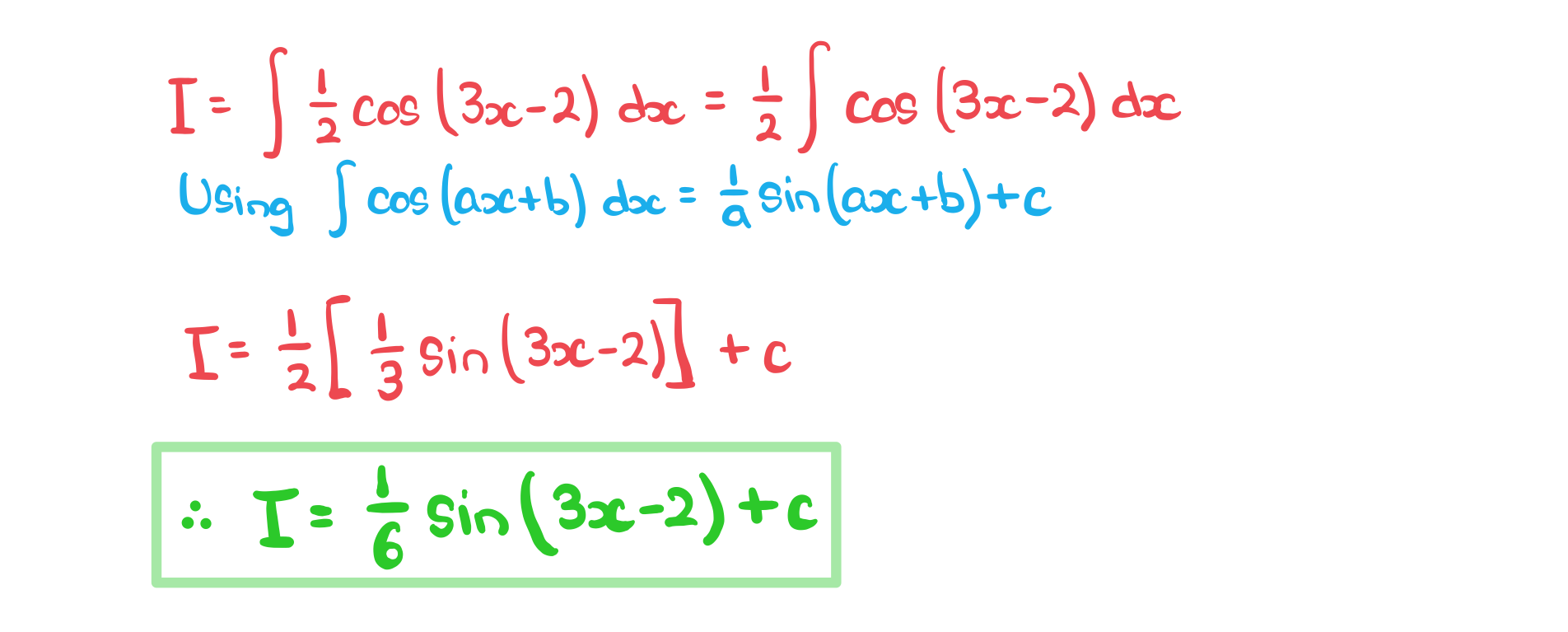
Reverse Chain Rule
What is reverse chain rule?
- The Chain Rule is a way of differentiating two (or more) functions
- Reverse Chain Rule (RCR) refers to integrating by inspection
- spotting that chain rule would be used in the reverse (differentiating) process
How do I know when to use reverse chain rule?
- Reverse chain rule is used when we have the product of a composite function and the derivative of its second function
- Integration is trickier than differentiation; many of the shortcuts do not work
How do I integrate using reverse chain rule?
- If the product can be identified, the integration can be done “by inspection”
- there may be some “adjusting and compensating” to do
- Notice a lot of the "adjust and compensate method” happens mentally
- this is indicated in the steps below by quote marks
Exam Tip
- Before the exam, practice this until you are confident with the pattern and do not need to worry about the formula or steps anymore
- This will save time in the exam
- You can always check your work by differentiating, if you have time
Worked Example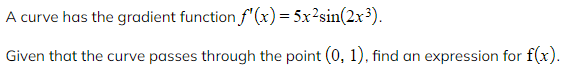
Substitution: Reverse Chain Rule
What is integration by substitution?
- When reverse chain rule is difficult to spot or awkward to use then integration by substitution can be used
How do I integrate using substitution?
Exam Tip
- Use your GDC to check the value of a definite integral, even in cases where working needs to be shown
Worked Example
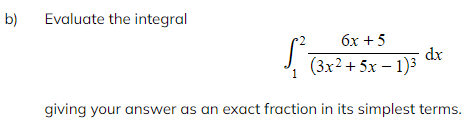
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
