- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel IGCSE Physics 复习笔记 1.4.2 The Principle of Moments
Edexcel IGCSE Physics 复习笔记 1.4.2 The Principle of Moments
The Principle of Moments
- The principle of moments states that:
If an object is balanced, the total clockwise moment about a pivot equals the total anticlockwise moment about that pivot
- Remember that the moment = force × distance from a pivot
- The forces should be perpendicular to the distance from the pivot
- For example, on a horizontal beam, the forces which will cause a moment are those directed upwards or downwards
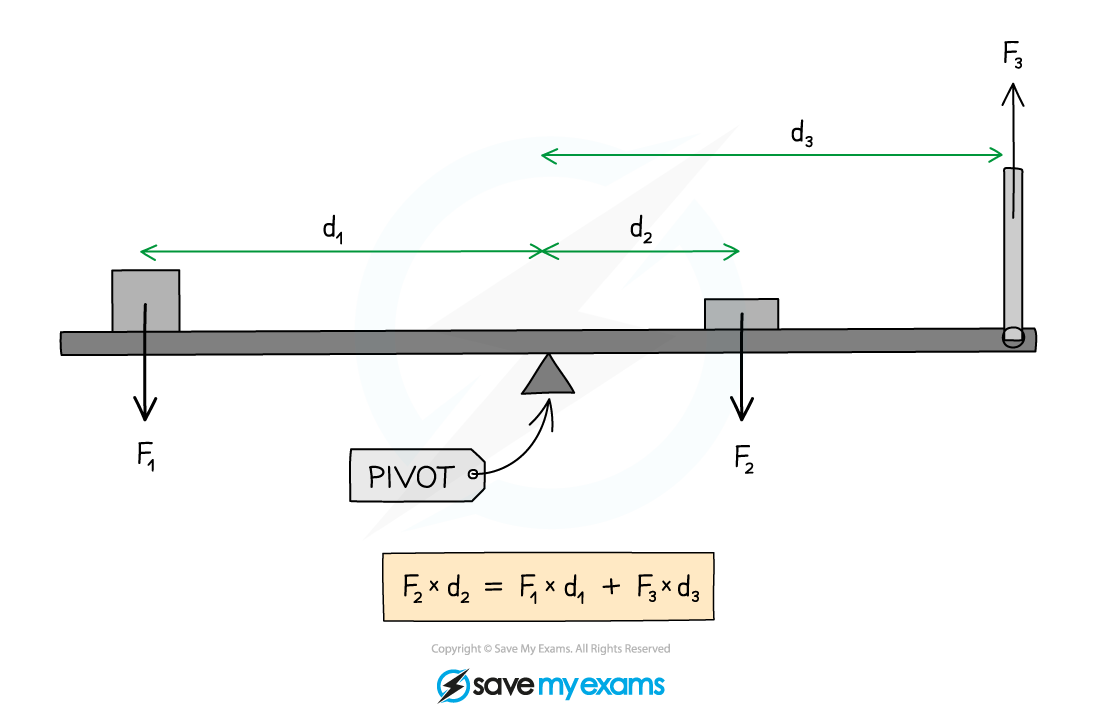
Moments on a balanced beam
- In the above diagram:
- Force F2 is supplying a clockwise moment;
- Forces F1 and F3 are supplying anticlockwise moments
- Due to the principle of moments, if the beam is balanced
Total clockwise moments = Total anticlockwise moments
- Hence:
F2 × d2 = (F1 × d1) + (F3 × d3)
Worked Example
A parent and child are at opposite ends of a playground see-saw. The parent weighs 690 N and the child weighs 140 N. The adult sits 0.3 m from the pivot.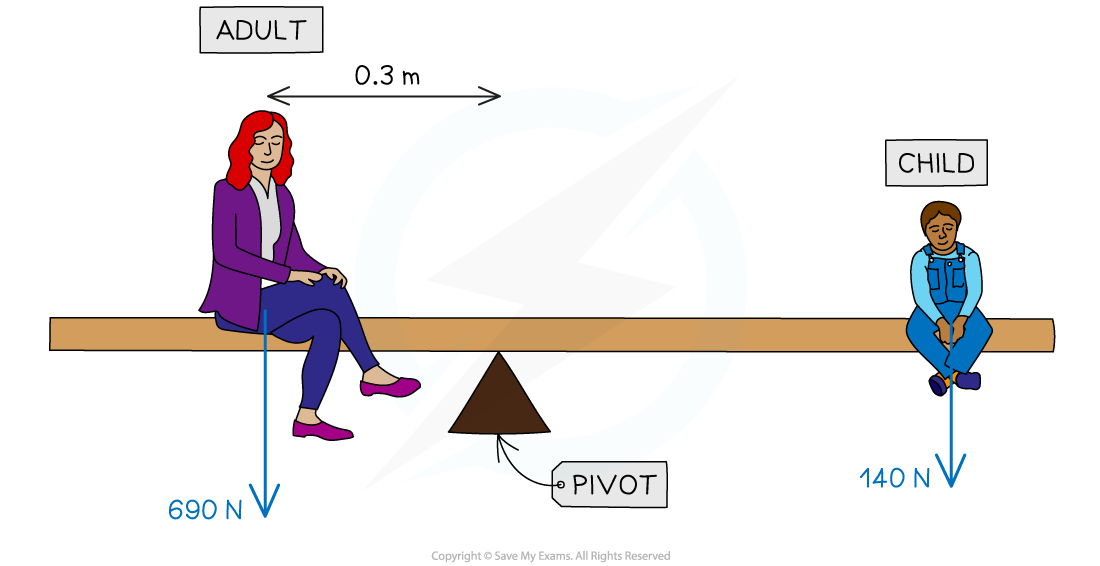 Calculate the distance the child must sit from the pivot for the see-saw to be balanced.
Calculate the distance the child must sit from the pivot for the see-saw to be balanced.
Step 1: List the know quantities
-
- Clockwise force (child), Fchild = 140 N
- Anticlockwise force (adult), Fadult = 690 N
- Distance of adult from the pivot, dadult = 0.3 m
Step 2: Write down the relevant equation
Moment = force × distance from pivot
-
- For the see-saw to balance, the principle of moments states that
Total clockwise moments = Total anticlockwise moments
Step 3: Calculate the total clockwise moments
-
- The clockwise moment is from the child
Momentchild = Fchild × dchild = 140 × dchild
Step 4: Calculate the total anticlockwise moments
-
- The anticlockwise moment is from the adult
Momentadult = Fadult × dadult = 690 × 0.3 = 207 Nm
Step 5: Substitute into the principle of moments equation
140 × dchild = 207
Step 6: Rearrange for the distance of the child from the pivot
dchild = 207 ÷ 140 = 1.48 m
Exam Tip
Make sure that all the distances are in the same units and you’re considering the correct forces as clockwise or anticlockwise, as seen in the diagram below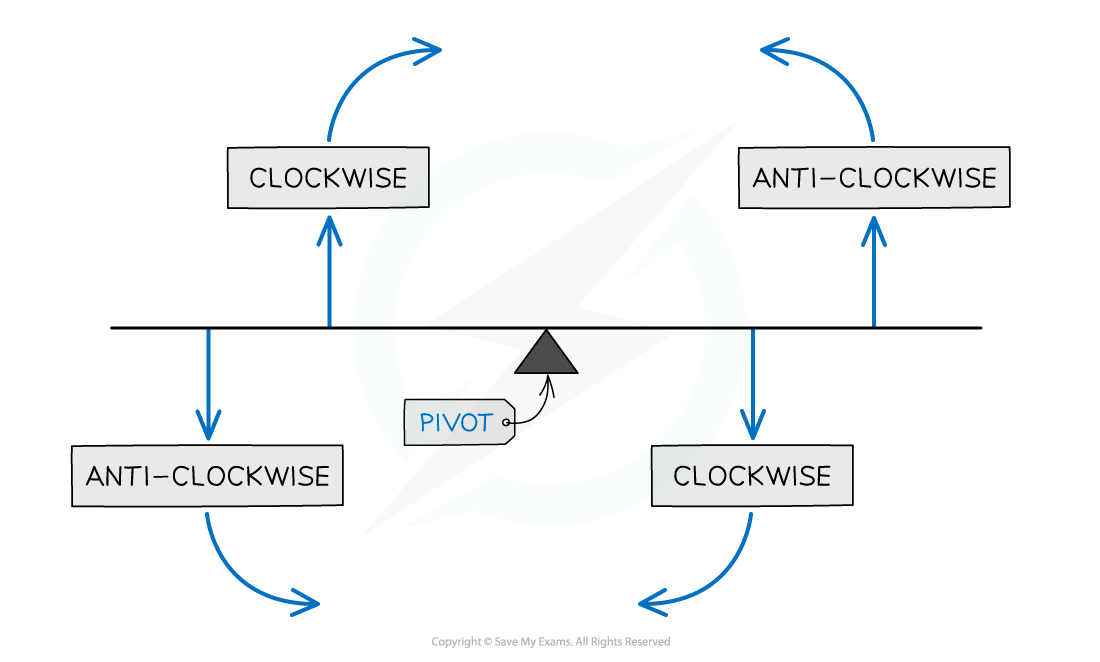 Clockwise is defined as the direction the hands of a clock move (and anticlockwise as the opposite)
Clockwise is defined as the direction the hands of a clock move (and anticlockwise as the opposite)
Supporting a Beam
- A light beam is one that can be treated as though it has no mass
- The supports, therefore, must supply upwards forces that balance the weight of any object placed on the beam
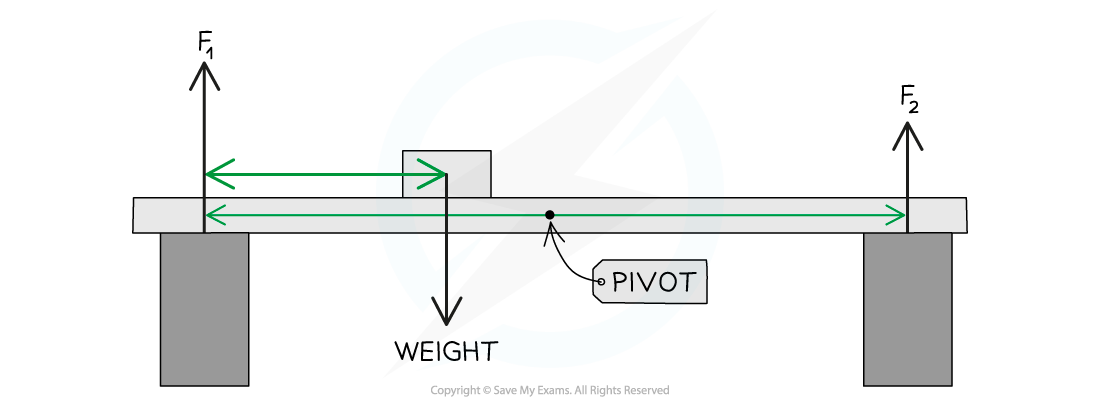
F1 and F2 upwards balance the weight of the beam downwards
- As the mass in the above diagram is moved from the left-hand side to the right-hand side of the beam, force F1 will decrease and force F2 will increase
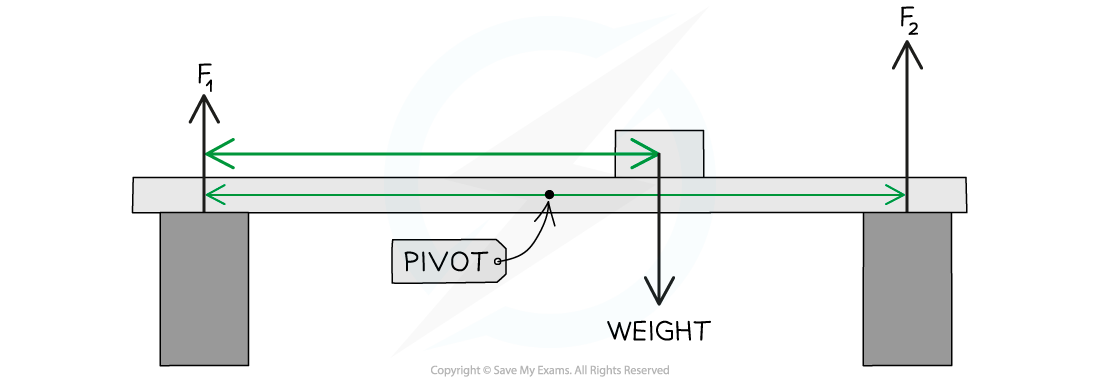
F1 decreases F2 increases keep the beam balanced
- Consider what would happen to the beam if the right-hand support was removed:
- Force F2 would be 0
- The weight of the object would supply a moment about the left-hand support, causing the beam to pivot in a clockwise direction
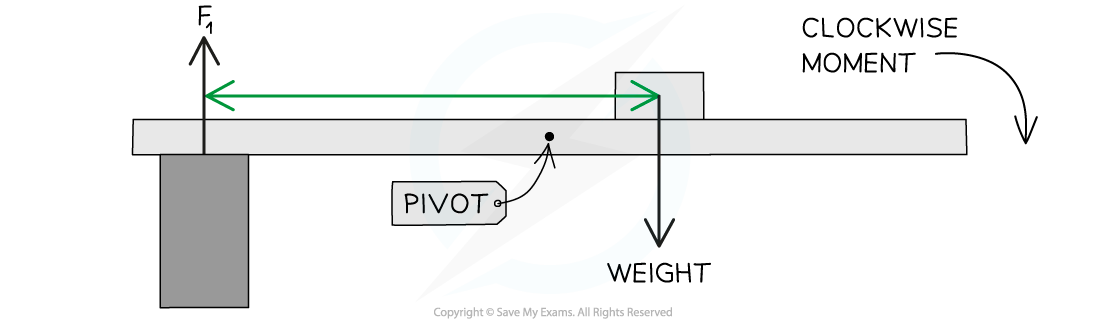
When F2 is removed the beam will rotate by the clockwise moment
- Therefore, the force F2 must therefore supply an anticlockwise moment about the left-hand support, which balances the moment supplied by the object
转载自savemyexam

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








