AQA A Level Maths: Mechanics复习笔记3.3.3 Coefficient of Friction - F = ma
Coefficient of Friction - F = ma
How do we apply Newton’s Second Law (F = ma) in problems involving friction?
- The coefficient of friction combined with F = ma allows you to determine an object's motion where friction is involved in a problem
- For problems where the surface is horizontal:
- Step 1. If necessary, resolve any angled forces into vertical and horizontal components
- Step 2. Calculate the normal reaction force R
- Be careful – if there are vertical forces other than gravity these will affect the value of R
- with a horizontal surface R will always be directed vertically upwards
- the magnitude of R will be such as to make the total vertical force on the object zero
- Step 3. Calculate FMAX= μR and find the resultant (total force) of all the horizontal forces on the object
- Remember – if the resultant of the other horizontal forces is less than or equal to FMAX then friction will exactly balance those forces out and the object will remain stationary
- Step 4. Use F = ma to determine the acceleration of the object
- For non-horizontal surfaces see the notes on inclined planes
Worked Example
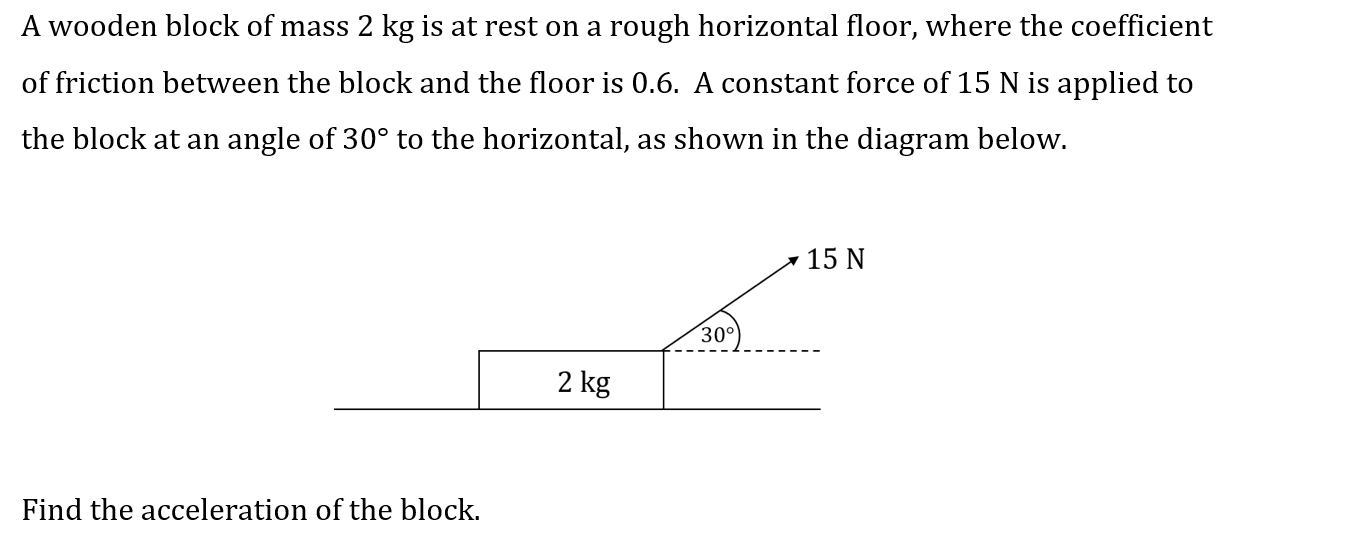
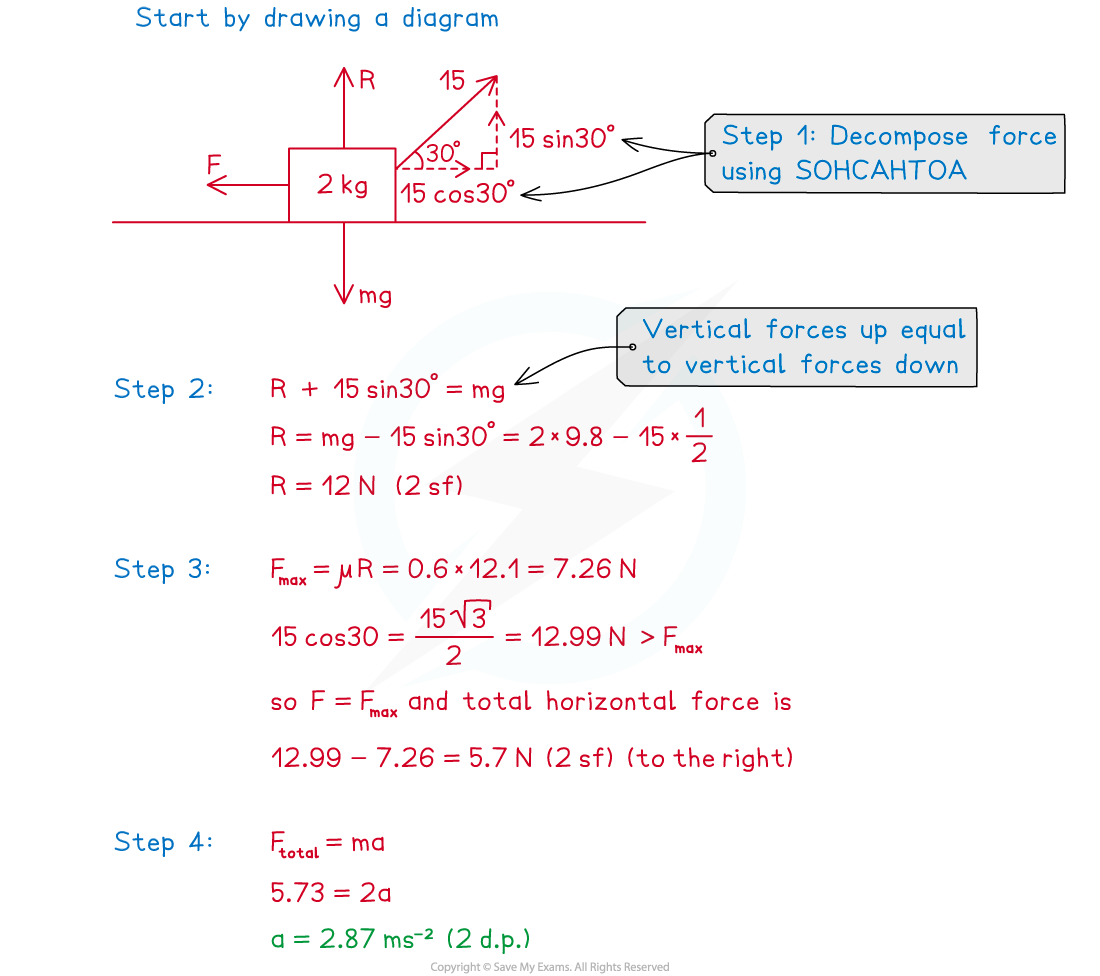
Find the acceleration of the block.
Exam Tip
- Always draw a force diagram and label it clearly.Look out for the words smooth and rough in mechanics problems involving an object moving (or potentially moving) along a surface:
- If the surface is described as smooth then you can ignore friction in the problem (ie μ= 0)
- If the surface is described as rough than you need to include the force of friction in solving the problem
- Be aware of whether the question is on a horizontal surface or an inclined plane.
- If g = 9.8 m s-2 has been used within a calculation then round that answer to 2 significant figures.
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
AMC8备考管家服务全新上线！
