备考攻略丨AP物理中典型的滑轮问题如何解决？

滑轮问题是典型的物理力学问题，不仅在AP physics的各门考试中出现，在IB考试和SAT2 physics考试中也经常出现。典型的滑轮问题：通常会给出物体质量，让同学们

计算释放之后物体的加速度（acceleration）a以及绳子中的张力（tension force)FT。（如下图）

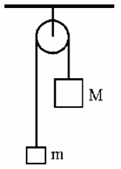
滑轮问题的特点是：包含多个研究对象，解决起来相对复杂。

滑轮问题又可以分为两种情况：滑轮质量可以忽略与滑轮质量不能忽略。

在讲解如何解决此两类问题之前，要先强调两点：

FT与物体的重力（weight）不相等

尽量不要采用整体法来研究此类问题

当研究一个复杂的问题的时候，我们的基本思路是将复杂问题转化成若干简单问题的叠加。有两层意思：首先，我们要将一个复杂的问题拆分成若干个简单的问题；其次，我们要找到这些简单问题之间的联系。

滑轮问题的复杂性体现在所需要研究的系统存在多个物体，要注意基本思路是：对每个物体单独做受力分析，并根据牛顿第二定律 Fnet=ma 列方程，然后找到各个物体之间的受力与运动之间的联系。

接下来，分别针对两种不同情况进行分析:

1、当滑轮质量可以忽略的时候

此种情况相对简单，因为滑轮没有质量，所以滑轮两边的FT相等，可以看做是m与M之间的相互作用力（action-reaction）。这就是物体之间受力的联系。每个物体都受到两个力的作用——FT和自身的重力（weight）。

但是，因为当物体被释放时，两个物体都在做加速运动，所以此二力不相等（注意！）。

另外，由于绳子的长度不变，所以两个物体的a大小相等。这就是物体之间运动的联系。

由此，我们可以根据牛顿第二定律列出下面的两个方程：

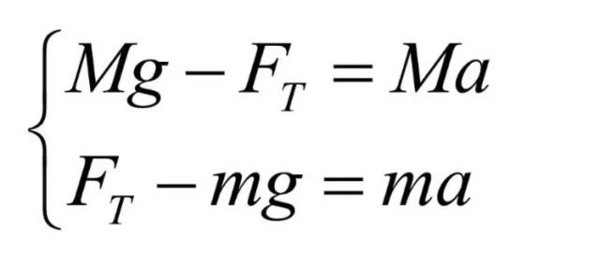
其中只有两个未知数——FT与a，此题可解。

同学们在做题的时候比较容易犯的错误是误将FT当作与mg相等，从而得出错误答案。其错误的本质是希望只通过列一个方程就解出答案。但是在研究类似的复杂问题的时候，我们往往需要列出多个方程。

另外，有的同学希望可以用整体法来解此类问题，即将m与M看做一个整体，这样可以只列出一个方程：Mg-mg=（M＋m）a 就解出a，但并不建议大家这样做。

原因是这样看似简单，却容易出错，而且只能计算出a，如果要计算FT还是要再列方程求解；更重要的是，这种方法只能在滑轮质量忽略不计的情况下使用，如果考虑到滑轮存在质量的情况，此种方法就不适用了。接下来，我们就来讨论一下这种情况。

2、当滑轮质量不能忽略

当滑轮的质量Mpulley不能忽略时，m与M在做平动运动（linear motion），滑轮在做转动运动（rotational motion）。

当我们研究滑轮的转动时，要考虑到滑轮存在转动惯量（moment of inertia）I（通常滑轮可以看做圆盘，所以 I=(1/2)MpulleyR?2; 其中R为滑轮半径）以及角加速度（angular acceleration）α，根据转动动力学（rotational dynamics)τnet=Iα, 作用在滑轮上的静力矩（net torque）不能为0，故此时滑轮两端的FT大小不相等。

这也就是整体法不适用的原因。

这里我们假设与m和M相连的绳子中的张力分别为FTm和FTM，所以作用在滑轮上的

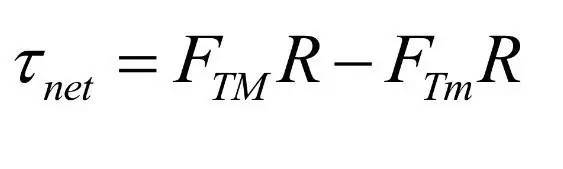
（同一段绳子上的张力相等）。这就是物体之间受力的联系。

由于绳子长度不变，所以两个物体的a大小仍然相等。而且，物体的a就等于绳子上任意一点的a（包括与滑轮接触的点），如果绳子不打滑，绳子上与滑轮接触的点与滑轮边缘上的点应该具有相同的a。

根据平动与转动的关系，我们可以得出a=αR。这就是物体之间运动的联系。

由此，我们可以根据牛顿第二定律、转动动力学和平动与转动的关系列出下面的四个方程：

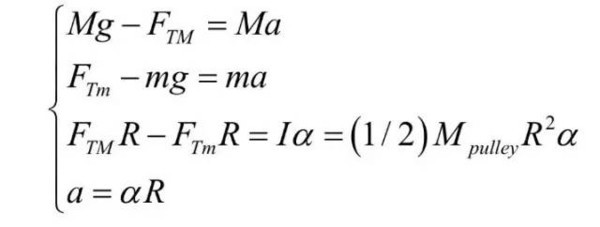
其中只有四个未知数——FTM 、FTm、 a 与α此题可解。同学们在解决这类问题的时候比较容易犯的错误是忽略了滑轮的转动效果，错认为滑轮两端的FT相等，将其当作第一种情况来解答，从而得出错误答案。

所以同学们在做滑轮问题的时候一定要把题目条件看清楚（主要是滑轮是否有质量）。当然，在接触滑轮问题的时候也可能会碰到其他的情况。

比如：其中一个物体放置在水平桌面上（甚至是斜面上）；滑轮是由两个半径不同的圆盘粘合而成；需要通过能量的方法来计算物体的速度等等。

不管问题怎么变化，我们基本的解题方法是相同的：首先，对每个物体单独进行受力分析，并根据

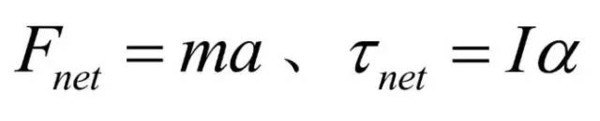
能量守恒（conservation of energy）等物理学规律针对每个物体列方程；

其次，找到物体之间受力的联系，主要依据是牛顿第三定律（action-reaction）；

最后，找到物体之间运动的联系：根据绳长不变可得出做平动运动的物体位移（displacement）、速度（velocity）、加速度（acceleration）大小相等，根据平动与转动之间的关系可得出a=αR、v=ωR（其中ω为转动角速度angular velocity）等等。